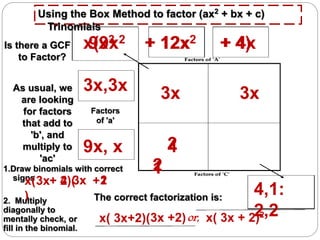
The document provides notes and examples on factoring trinomials of the form (ax^2 + bx + c) where a is greater than 1. It discusses three methods: grouping, using a box method, and trial and error. Students are reminded to complete their Khan Academy assignments by that night and that there will be new topics on Monday. They are also instructed to do the class work and study guide questions to prepare for their test.

1. Today:
 Warm-Up:
Review Monday's Topics & Friday's Test
 Continue: Factoring (ax2
+ bx + c) Trinomials
 Reminder: Khan Academy Due by Tonight, New
Topics Monday
 Class Work
25

2. Warm-Up: Test Review(8)
3. 9/49x² - 4
1. (1/2x - y)(1/2x + y) 2. x² - 1/16 2. (x - 1/4)(x + 1/4)
3. (3/7x+2)(3/7x- 2) 4. x2 + 8x - 48
7. x2
- 10xy + 25y2
1. 1/4x² - y²
4. (x + 12) (x - 4)
Factor or expand each expression completely:
5. (2x + 3y)² 5. (4x² + 12xy + 9y²) 6. (.25a – .36b)²
6. (.5a + .6b)(.5a - .6b)
Class Notes Section of your Notebook:
8. (x2
+ 9y)² 8. (x4
+ 18xy + y2
)
7. (x - 5y)2

3. Perfect Square Trinomial
1. PST's have a square in the first & third terms: The
first & third terms are always positive.
2. The factors of PST's are always either the square
of a sum (x + y)², or the square of a difference (x - y)²
3. To determine whether a trinomial is a PST, one
of two tests need to be applied. They are:
The middle term is twice the product of
the square root of the first term and the
square root of the third term.
or b 2
2
must = A*C
Recognizing & Factoring Perfect Square Trinomials

4. Factoring 2nd degree trinomials
with a leading coefficient > 1
Factoring (ax2
+ bx + c) Trinomials

5. Method #1: Grouping

6. Step
1
Multiply the leading coefficient and the constant
term
Method #1: Grouping
25x2 + 20x + 4
25 • 4 = 100

7. Step 2
Find the two factors of 100 that add to
the coefficient of the middle term.
Notice the 'plus, plus' signs in the
original trinomial.
Factors of 100:
1 100
2 50
4 25
5 20
10 10
Our two factors are10 &
10
25x2 + 20x + 4

8. Step 3
Re-write the original trinomial
and replace 10x with 6x + 4x.
Step
4 Factor by Grouping
25x2 + 20x + 4
25x2 + 10x + 10x + 4
(25x2 + 10x) + (10x + 4)

9. Step
5 Factor out the GCF of each pair of
terms
After doing so, you will have...
Step
6 Factor out the common binomial.
(25x2 + 10x) + (10x + 4)
5x(5x + 2) + 2(5x + 2)
(5x + 2)(5x + 2)
Pair the remaining terms together.
The final factorization is? A PST!(5x + 2)2
A 5 second check before solving saves time
and possibly incorrect factoring.

10. Practice: Factor by Grouping
Factor: 30x2 - 27x + 6In this case, step 1 is...
and we are left with.. 3(10x2 - 9x + 2)
1 20
2 10
4 5
Multiply the leading coefficient and the constant
termFactors of 20: Our two factors are 4 & 5
Re-write the original trinomial
and replace -9x with -4x & -5x.
3(10x2
- 5x - 4x +
2)Factor by Grouping 3(10x2
- 5x) -
?3 • 5x(2x - 1) - 2(2x - 1)
=
3(2x - 1)(5x -
2)
Factor
the GCF
The signs of the factors will be: ( - ) ( - )
(4x - 2) =

11. Method #2: The Box Method

12. Using the Box Method to factor (ax2
+ bx + c)
Trinomials
9x3 + 12x2 + 4x
As usual, we
are looking
for factors
that add to
'b', and
multiply to
'ac'
Is there a GCF
to Factor?
x(9x2 + 12x + 4)
3x,3x
9x, x
4,1:
2,2
3x 3x
1.Draw binomials with correct
signs
4
1
x( + )( +
)2. Multiply
diagonally to
mentally check, or
fill in the binomial.
3x 4 3x 13x 2 3x 2
x( 3x+2)(3x +2)or,
The correct factorization is:
x( 3x + 2)2
Factors
of 'a'
2
2

13. Practice: Factor using the Box Method
10x2 + 21x -
10
10,-1: -
10,1
5,-2: -5,2
10x,x
5x,2x
Factors
of 'a'
Draw binomials with correct
signs( - )( +
)
( 2x+5)(5x- 2)
5x 2x
-5 2
That doesn't work, so we'll
try
-2 5

14. Method #3: Trial & Error

15. Task: Factor the polynomial (25x2 +101x + 4)
Possible factors of 25x2 are
Possible factors of 4 are
We need to try each pair of factors until we find a
combination that works, or exhaust all of our possible
pairs of factors.
Keep in mind that, because some of our pairs are not
identical factors, we may have to switch some pairs of
factors and make 2 attempts before we can definitely
decide a particular pair of factors will not work.
Method #3: Trial & Error
{x, 25x} or {5x, 5x}.
{1, 4} or {2, 2}.

16. We are looking for a combination that gives the sums to
the middle term and are factors of the last term
{5x, 5x} {2, 2} (5x + 2)(5x + 2)
Method #3: Trial & Error
{x, 25x} {2, 2} (x + 2)(25x + 2)
10x 10x 20x
4x 25x 29x
2x 50x 52x
x 100x 101x
(25x2 +101x + 4)
(x + 4)(25x + 1)
{x, 25x} {1, 4} (x + 1)(25x + 4)

17. Class Work: 3.10 & Study Guide
for Test
1. If you want to keep the handout for class work 3.10,
write the questions on separate sheet of paper
2. Try to solve the questions on the study guide, as the
test will look very similar.
On Class Work 3.10, Replace questions 11, 12, 13, 15 with
3. x2 - 11x + 24 4. 32 - 8z2
5. 3a2 - 24ab + 48b2 6. v2q2 - .49r2