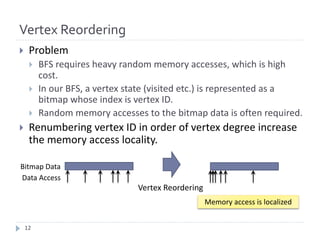
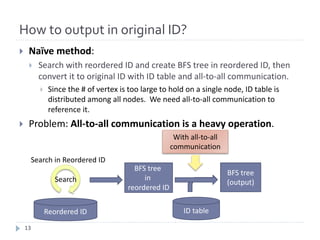
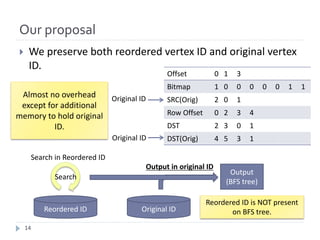
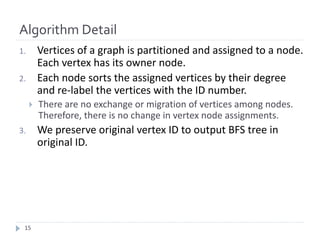
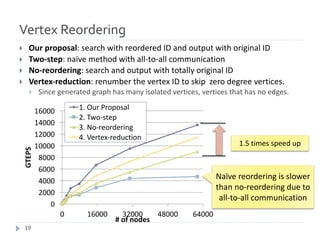
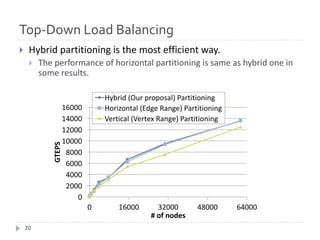
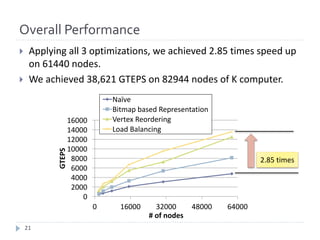
The document discusses advancements in efficient breadth-first search (BFS) algorithms for large-scale supercomputers, focusing on techniques such as bitmap-based sparse matrix representation, vertex reordering, and load balancing. The proposed methods resulted in a significant performance increase, achieving 38,621 giga traversed edges per second on the K computer, which contributes to its top ranking in the Graph500 benchmark. The authors address challenges in partitioning and accessing hyper sparse matrices while introducing innovative solutions that enhance computational efficiency.

1. Extreme Scale Breadth-First Search on
Supercomputers
Tokyo Institute ofTechnology / RIKEN
IBMT.J.Watson Research Center
RIKEN
Kyushu University
Tokyo Institute ofTechnology / AIST
Koji Ueno
Toyotaro Suzumura
Naoya Maruyama
Katsuki Fujisawa
Satoshi Matsuoka

2. Large-Scale Graph Mining is Everywhere
Symbolic Networks: Human
Brain: 100 billion neuron
Protein Interactions
[genomebiology.com]
Social Networks[Moody ’01]
（Facebook: 1 billion users) Cyber Security ( 15 billion log
entries / day for large enterprise)
Cybersecurity
Medical Informatics
Data Enrichment
Social Networks
Symbolic Networks
WWW[lumeta.com]
（1 trillion unique URL)
2

3. Breadth First Search on Large Distributed Memory
Machines
} Breadth First Search (BFS):
} The most fundamental graph algorithm.
} A kernel of Graph500 benchmark.
} Large scale supercomputers:
} Consists of thousands of distributed memory nodes.
} How to compute graph algorithms efficiently on those
machines is an attacking challenge.
K Computer: 83,000 nodesTSUBAME2.5: 1400 nodes
3

4. Graph500 Benchmark [http://www.graph500.org/]
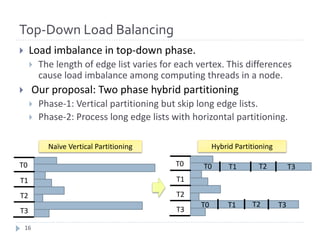
} One of our major targets is Graph500 benchmark.
} Benchmark for Big Data (data intensive) applications.
} BFS is a main kernel for ranking.
} K computer is #1 using our result.
Graph500 Latest Ranking
4

5. Breadth First Search（BFS）
RootRoot
Level 1
Level 2
Level 3
BFS
Input: Graph and Root Vertex Output: BFS Tree
5

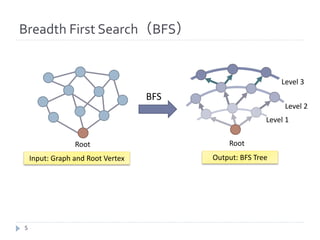
6. Direction Optimization [Beamer, ’11-12]
} Direction optimization is an fast BFS algorithm which switches
direction (Top-Down and Bottom-Up) for each searching level.
} Direction optimization is effective for small diameter graphs.
} Scale free networks and small world networks are small diameter
graphs.
} The target of Graph500 benchmark is also small diameter
graph and direction optimization is effective.
Frontier
Neighbors
Level k
Level k+1
Frontier
Level k
Level k+1
Neighbors
Top-Down Bottom-Up
6

7. 2D Partitioning BFS
} Two dimensionally partition the adjacency matrix for graph
} Each partitioned region is assigned to each node.
} Nodes are virtually spread on a 2D mesh.
} Advantages of 2D partitioning over 1D partitioning
} Partitioned matrix region is near square. Rows and columns of this
region is not too large to hold the related data locally. Whereas, in
1D partitioning, we cannot hold all the data related to rows and
columns of the partitioned matrix region. The data of rows or
columns are distributed among nodes, which required additional
communication.
7

8. RelatedWork
} Distributed BFS with Top-Down only:
} 2D Partitioning BFS on BlueGene/L [Yoo ‘05]
} Proposed Distributed Memory BFS on Large Distributed Memory
} Comparison of 1D Partitioning and 2D Partitioning [Buluc ‘11]
} Distributed Memory BFS on Commodity Machine (Intel CPU and
Infiniband network) [Satish ‘12]
} Distributed BFS with Direction Optimization
} 2D Partitioning BFS with Direction Optimization [Beamer ’13]
} Our proposed BFS is based on their BFS.
} 1D Partitioning BFS with Direction Optimization and Load Balancing.
[Checconi ‘14]
} This is very scalable and they achieved 23751 GTEPS on BlueGene/Q 98304 Nodes.
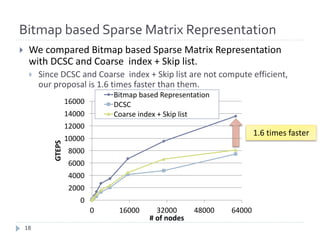
} They Proposed novel sparse matrix representation “Coarse index + Skip list”.
However, our bitmap based sparse matrix representation is more efficient.
8

9. Problem of Graph Data Structure
} When we partition graphs for large supercomputers, a
partitioned matrix is a Hyper Sparse Matrix.
} How do we represent this Hyper Sparse Matrix?
・・・
・・・
256
256
Hyper Sparse
Matrix
Partition a Graph into
65,536 Partitions
9

10. Existing Approaches for Sparse Matrix
} Traditional approach:
} Compressed Sparse Row (CSR)
} CSR is NOT memory efficient for hyper sparse matrix
Source(SRC) 0 0 6 7
Destination(DST) 4 5 3 1
Row Offset 0 2 2 2 2 2 2 3 4
DST 4 5 3 1
・Edge List ・CSR
Partitioned Graph Adjacency Matrix: 8 Vertex and 4 Edge
Memory wasted
} For Hyper Sparse Matrix:
} DCSR (DCSC)
} Coarse Index + Skip List
} These approaches are NOT compute efficient.
} We demonstrate at the performance evaluation.
Example
10

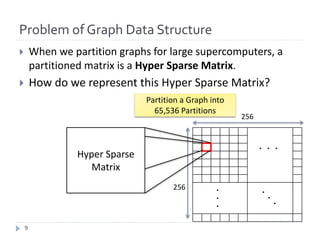
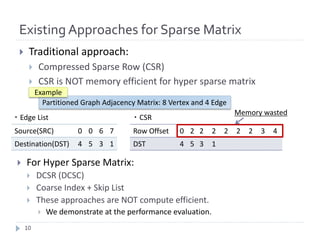
11. Bitmap based Sparse Matrix Representation
SRC 0 0 6 7
DST 4 5 3 1
・Edge List
Offset 0 1 3
Bitmap 1 0 0 0 0 0 1 1
Row Offset 0 2 3 4
DST 4 5 3 1
・Bitmap base Sparse Matrix
Only consumes 8 bits
} Structure
} Row Offset: Skip vertices that has no edges (same as DCSC)
} Bitmap: one bit for each vertex: represents the vertex has at least one edge (set
bit) or not (not set bit).
} Offset: Supplemental array for faster computing: Represents cumulative # of set
bits from the beginning of bitmap to the corresponding word boarder.
} How to compute the row offset index of a given vertex?
} Row offset index = Offset[w] + popcount(Bitmap[w]&mask)
} Where w = v / 64, mask = (1 << (v % 64)) – 1, v is index of a given vertex.
} This is no loop. Therefore, this is an O(1) operation, which is same as CSR.
In this example, 1 word is 4 bit.
Partitioned Graph Adjacency Matrix: 8 Vertex and 4 Edge
Example
11

12. Vertex Reordering
} Problem
} BFS requires heavy random memory accesses, which is high
cost.
} In our BFS, a vertex state (visited etc.) is represented as a
bitmap whose index is vertex ID.
} Random memory accesses to the bitmap data is often required.
} Renumbering vertex ID in order of vertex degree increase
the memory access locality.
12
Vertex Reordering
Bitmap Data
Data Access
Memory access is localized

13. How to output in original ID?
Reordered ID ID table
BFS tree
(output)
} Naïve method:
} Search with reordered ID and create BFS tree in reordered ID, then
convert it to original ID with ID table and all-to-all communication.
} Since the # of vertex is too large to hold on a single node, ID table is
distributed among all nodes. We need all-to-all communication to
reference it.
} Problem: All-to-all communication is a heavy operation.
BFS tree
in
reordered ID
With all-to-all
communication
Search in Reordered ID
Search
13

14. Our proposal
} We preserve both reordered vertex ID and original vertex
ID.
Reordered ID Original ID
Search
Output
(BFS tree)
Search in Reordered ID
Output in original ID
Reordered ID is NOT present
on BFS tree.
Offset 0 1 3
Bitmap 1 0 0 0 0 0 1 1
SRC(Orig) 2 0 1
Row Offset 0 2 3 4
DST 2 3 0 1
DST(Orig) 4 5 3 1
Original ID
Original ID
Almost no overhead
except for additional
memory to hold original
ID.
14

15. Algorithm Detail
1. Vertices of a graph is partitioned and assigned to a node.
Each vertex has its owner node.
2. Each node sorts the assigned vertices by their degree
and re-label the vertices with the ID number.
} There are no exchange or migration of vertices among nodes.
Therefore, there is no change in vertex node assignments.
3. We preserve original vertex ID to output BFS tree in
original ID.
15

16. Top-Down Load Balancing
} Load imbalance in top-down phase.
} The length of edge list varies for each vertex. This differences
cause load imbalance among computing threads in a node.
} Our proposal: Two phase hybrid partitioning
} Phase-1: Vertical partitioning but skip long edge lists.
} Phase-2: Process long edge lists with horizontal partitioning.
T0
T1
T2
T3
T0
T1
T2
T3
T0
T0
T1
T1
T2
T2
T3
T3
Naïve Vertical Partitioning Hybrid Partitioning
16

17. Performance Evaluation
} Evaluated performance of 3 proposed methods.
} Bitmap based Sparse Matrix
} Reordering Vertex ID
} Top-Down Load Balancing
} Using up to 61440 nodes of K computer.
} Weak scaling: # of vertices: 2^33 per 960 nodes
} # of edges: 16 x “# of vertices”
} Graph is generated by R-MAT generator.
} Parameter: A=0.57,B=0.19,C=0.19,D=0.05 (Same as Graph500
benchmark)
} Performance is a median of 300 BFS. (Each BFS starts from
each unique root vertex)
} Performance unit is TEPS: Traversed Edges Per Second
} GTEPS = Giga (1,000,000,000) TEPS
17

18. Bitmap based Sparse Matrix Representation
} We compared Bitmap based Sparse Matrix Representation
with DCSC and Coarse index + Skip list.
} Since DCSC and Coarse index + Skip list are not compute efficient,
our proposal is 1.6 times faster than them.
1.6 times faster
0
2000
4000
6000
8000
10000
12000
14000
16000
0 16000 32000 48000 64000
GTEPS
# of nodes
Bitmap based Representation
DCSC
Coarse index + Skip list
18

19. Vertex Reordering
} Our proposal: search with reordered ID and output with original ID
} Two-step: naïve method with all-to-all communication
} No-reordering: search and output with totally original ID
} Vertex-reduction: renumber the vertex ID to skip zero degree vertices.
} Since generated graph has many isolated vertices, vertices that has no edges.
1.5 times speed up
Naïve reordering is slower
than no-reordering due to
all-to-all communication
0
2000
4000
6000
8000
10000
12000
14000
16000
0 16000 32000 48000 64000
GTEPS
# of nodes
1. Our Proposal
2. Two-step
3. No-reordering
4. Vertex-reduction
19

20. Top-Down Load Balancing
} Hybrid partitioning is the most efficient way.
} The performance of horizontal partitioning is same as hybrid one in
some results.
0
2000
4000
6000
8000
10000
12000
14000
16000
0 16000 32000 48000 64000
GTEPS
# of nodes
Hybrid (Our proposal) Partitioning
Horizontal (Edge Range) Partitioning
Vertical (Vertex Range) Partitioning
20

21. Overall Performance
} Applying all 3 optimizations, we achieved 2.85 times speed up
on 61440 nodes.
} We achieved 38,621 GTEPS on 82944 nodes of K computer.
2.85 times
0
2000
4000
6000
8000
10000
12000
14000
16000
0 16000 32000 48000 64000
GTEPS
# of nodes
Naïve
Bitmap based Representation
Vertex Reordering
Load Balancing
21

22. Conclusion
} We proposed efficient Breadth First Search for large
distributed memory machines.
} We present 3 methods to speed up distributed BFS:
} Bitmap based Sparse Matrix Representation
} Reordering vertex ID without searching overhead
} Top-down load balancing
} We achieved 38,621 GTEPS on K computer, which ranked
top on Graph500 now from July 2015.
22