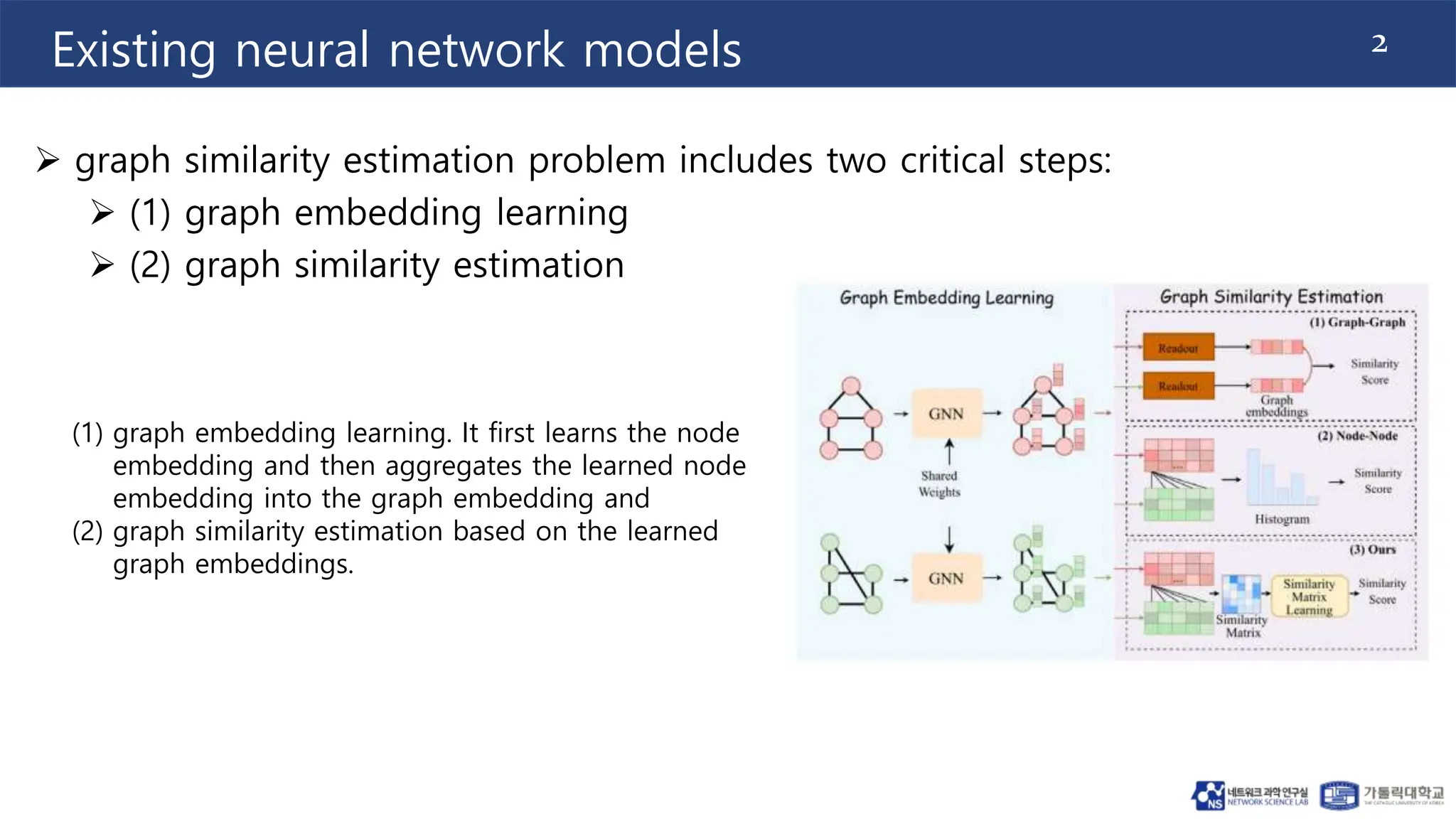
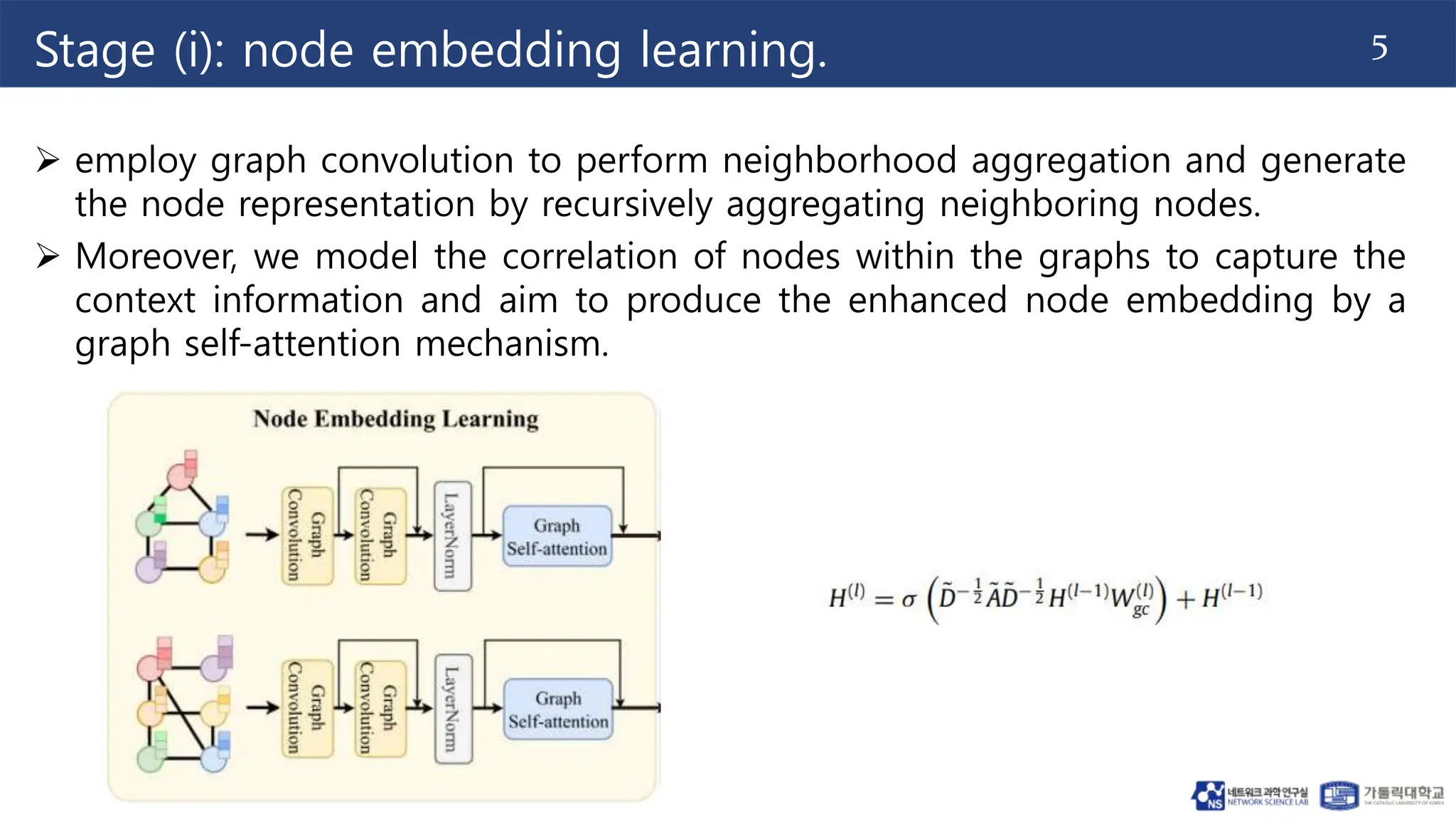
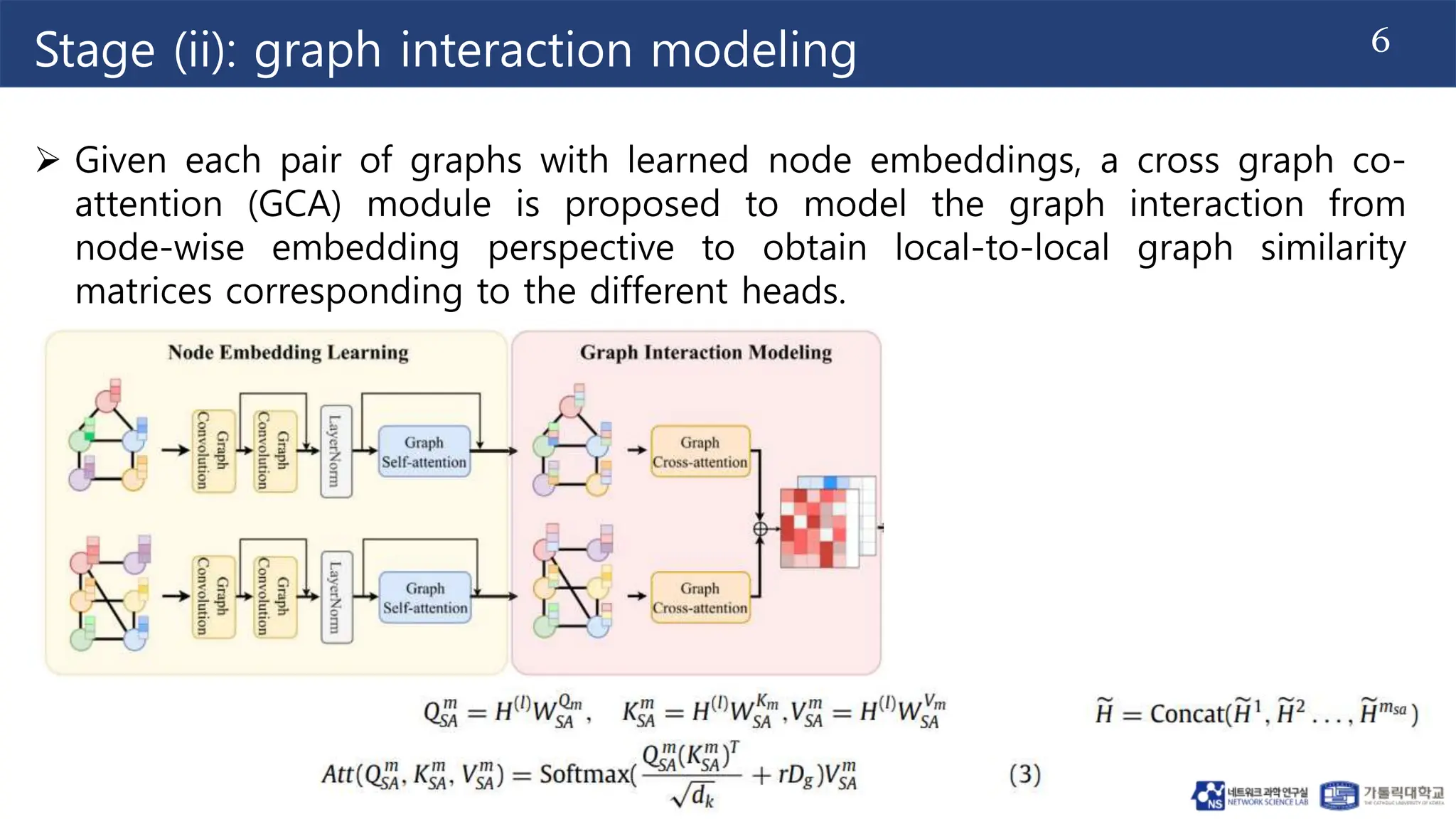
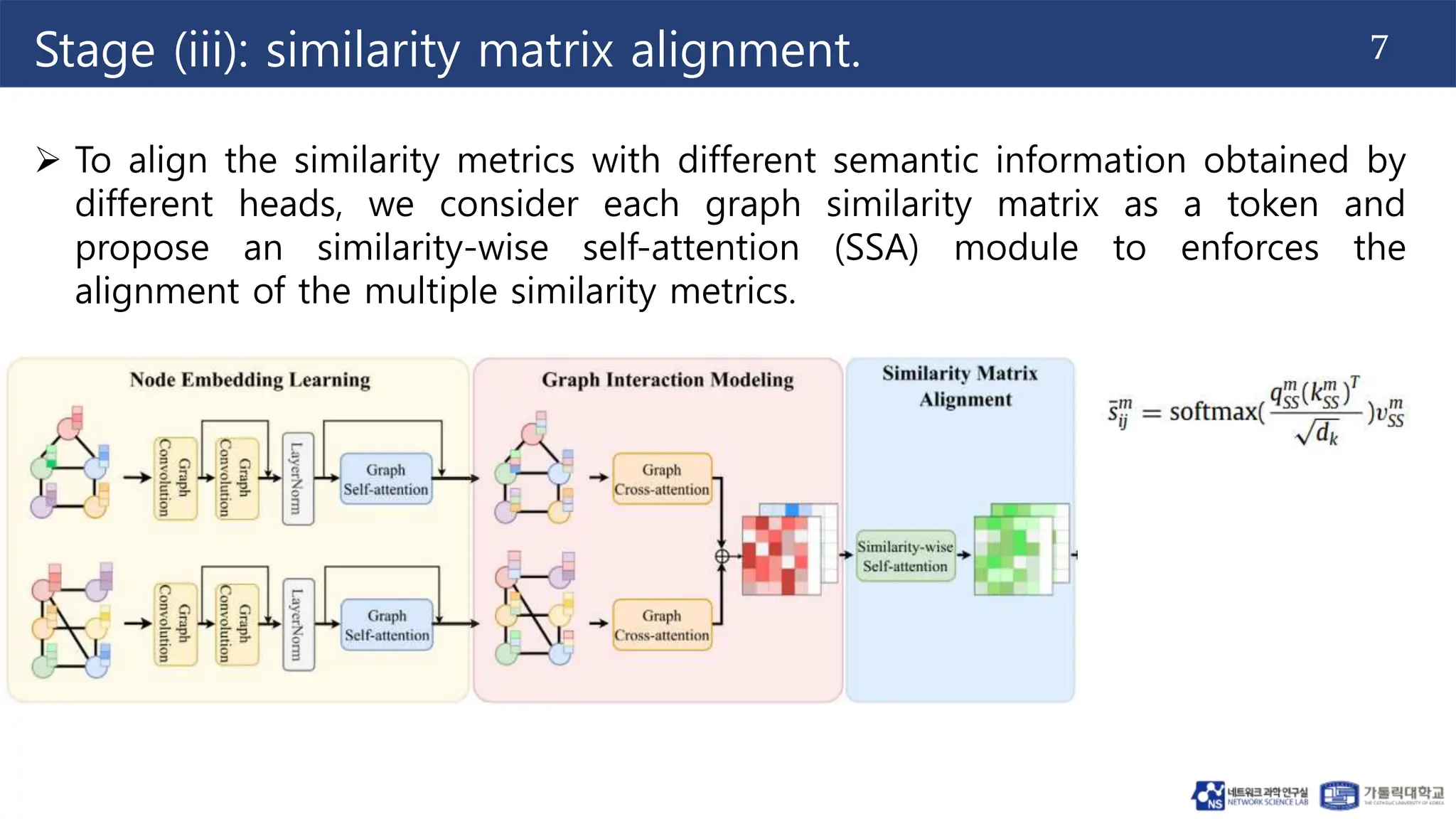
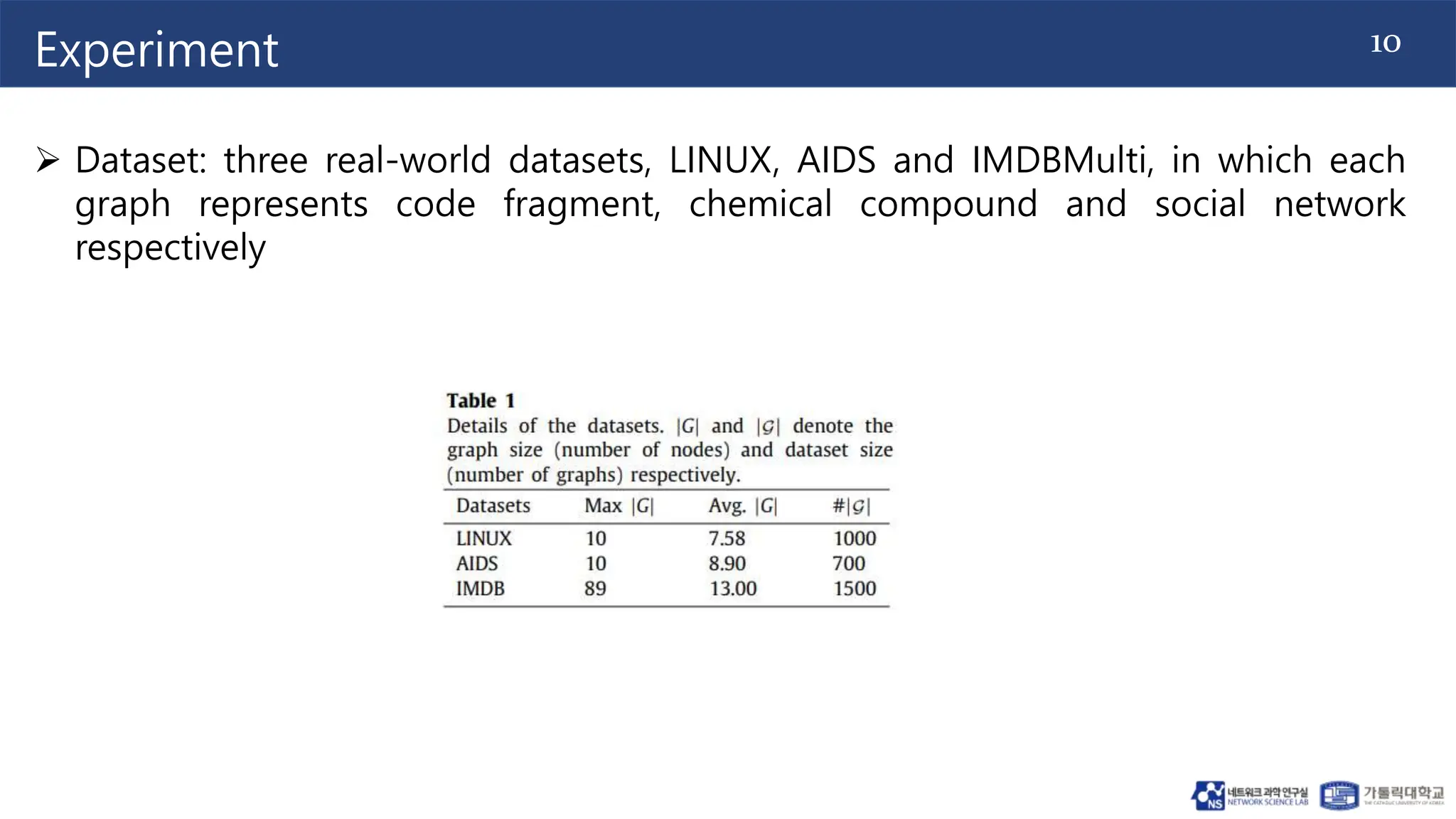
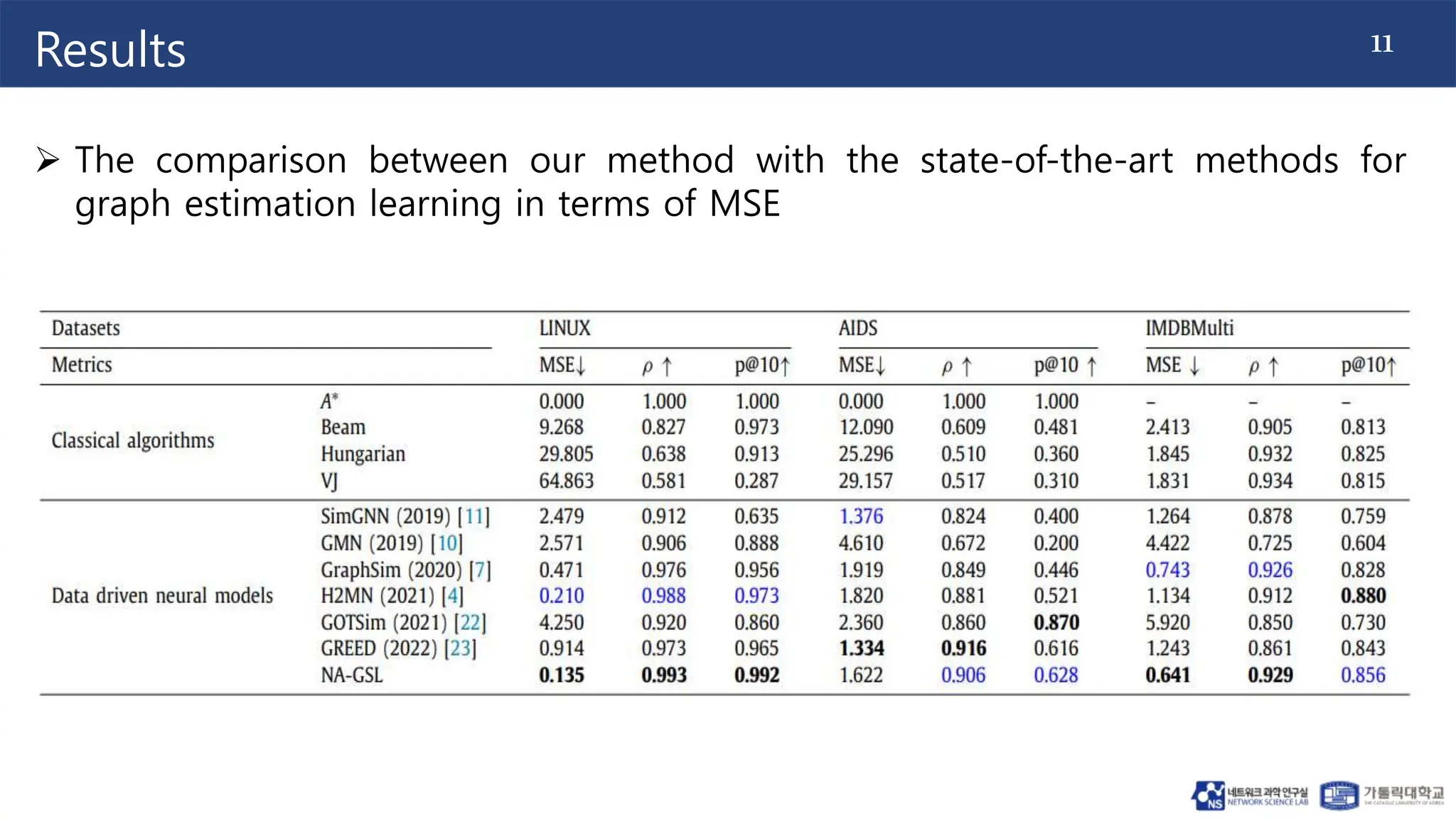
The document proposes a method for graph similarity learning using node-wise attention. It involves 4 stages: (1) node embedding learning using graph convolution, (2) graph interaction modeling using cross-graph co-attention, (3) similarity matrix alignment using similarity-wise self-attention, and (4) similarity matrix learning using a similarity structure learning module. The method is evaluated on three datasets and shown to outperform state-of-the-art methods according to mean squared error. Ablation experiments demonstrate the effectiveness of using different graph neural networks. The approach aims to improve graph similarity learning by encoding node features and structural properties using attention mechanisms.

1. Van Thuy Hoang
Network Science Lab
Dept. of Artificial Intelligence
The Catholic University of Korea
E-mail: hoangvanthuy90@gmail.com
2023-10-23
Wenhui Tan; Knowledge-Based Systems 23

2. 2
Existing neural network models
 graph similarity estimation problem includes two critical steps:
 (1) graph embedding learning
 (2) graph similarity estimation
(1) graph embedding learning. It first learns the node
embedding and then aggregates the learned node
embedding into the graph embedding and
(2) graph similarity estimation based on the learned
graph embeddings.

3. 3
Graph similarity learning

4. 4
Overview of Node-wise Attention guided Graph Similarity Learning
 X

5. 5
Stage (i): node embedding learning.
 employ graph convolution to perform neighborhood aggregation and generate
the node representation by recursively aggregating neighboring nodes.
 Moreover, we model the correlation of nodes within the graphs to capture the
context information and aim to produce the enhanced node embedding by a
graph self-attention mechanism.

6. 6
Stage (ii): graph interaction modeling
 Given each pair of graphs with learned node embeddings, a cross graph co-
attention (GCA) module is proposed to model the graph interaction from
node-wise embedding perspective to obtain local-to-local graph similarity
matrices corresponding to the different heads.

7. 7
Stage (iii): similarity matrix alignment.
 To align the similarity metrics with different semantic information obtained by
different heads, we consider each graph similarity matrix as a token and
propose an similarity-wise self-attention (SSA) module to enforces the
alignment of the multiple similarity metrics.

8. 8
Stage (iv): similarity matrix learning
 propose a similarity structure learning module (SSL) with considering the
topology structure and performing the co-embedding of nodes and edges to
map the similarity matrices into a graph–graph similarity score

9. 9
Loss function
 The Mean Square Error (MSE) as the final loss function, which is defined as
follow:

10. 10
Experiment
 Dataset: three real-world datasets, LINUX, AIDS and IMDBMulti, in which each
graph represents code fragment, chemical compound and social network
respectively

11. 11
Results
 The comparison between our method with the state-of-the-art methods for
graph estimation learning in terms of MSE

12. 12
Results
 Ablation experiment results on different GNNs

13. 13
CONCLUSION
 Developing data driven neural models for graph similarity learning is an
important research direction with many applications
 aim to improve the graph similarity learning from the node-wise perspective
through introducing multiple attention based modules.
 (1) graph embedding learning by encoding the features and structural
properties around each node
 (2) similarity computation based on these feature vectors.
 However, the graph embedding learning ignores the local structure around the
nodes, the graph similarity computation manner does not sufficiently model
the node interactions and capture the fine-grained local structure in the
similarity matrices. T