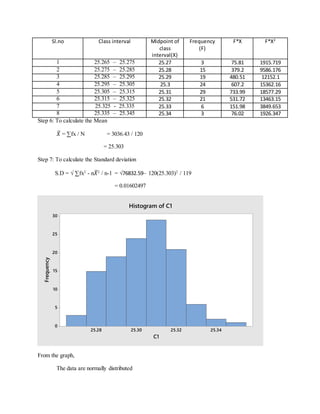
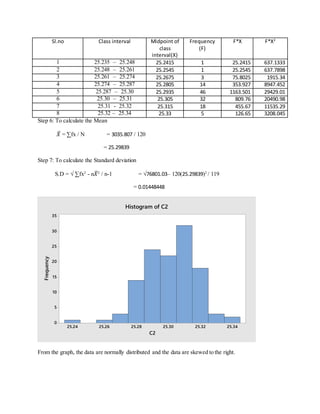
The document contains a table with 15 observations of 4 variables (X1, X2, X3, X4) measured for each of 3 datasets (a total of 120 observations). The mean, standard deviation, and distribution of the data were calculated for each dataset. For all datasets, the data were found to be normally distributed. Datasets 2 and 3 were skewed slightly to the right. The standard deviations ranged from 0.01 to 0.18, indicating little variance among the observations within each dataset.

1. Sl.no X1 X2 X3 X4
1 25.31 25.32 25.32 25.32
2 25.29 25.3 25.3 25.3
3 25.27 25.28 25.28 25.29
4 25.28 25.29 25.3 25.29
5 25.30 25.31 25.33 25.31
6 25.30 25.32 25.31 25.31
7 25.27 25.29 25.28 25.28
8 25.29 25.3 25.32 25.31
9 25.3 25.3 25.31 25.31
10 25.32 25.31 25.33 25.32
11 25.31 25.31 25.3 25.31
12 25.3 25.28 25.29 25.31
13 25.29 25.28 25.29 25.3
14 25.32 25.33 25.32 25.31
15 25.27 25.28 25.3 25.28
1 25.32 25.31 25.31 25.32
2 25.29 25.28 25.31 25.28
3 25.31 25.3 25.3 25.3
4 25.3 25.3 25.29 25.31
5 25.28 25.29 25.29 25.3
6 25.29 25.3 25.29 25.29
7 25.3 25.33 25.31 25.31
8 25.32 25.31 25.31 25.32
9 25.33 25.32 25.32 25.34
10 25.35 25.32 25.33 25.34
11 25.31 25.32 25.31 25.3
12 25.32 25.3 25.3 25.31
13 25.28 25.29 25.28 25.31
14 25.29 25.31 25.32 25.32
15 25.32 25.31 25.29 25.28

2. Step 1: Determine the total number of observations
N = 120
Step 2: Calculate the range of the data
Range = Maximum value – Minimum value
= 25.35- 25.27
= 0.08
Step 3: Determine the number of class intervals (k)
K = 1 + 3.33 log10(N)
= 1 + 3.33 log10(120)
= 8
Step 4: Determine the width of the class interval
Class interval = Range/K
= 0.08/8
= 0.01
Step 5: Construct the frequency distribution table
= Lowest value – ½(Least Count)
= 25.27 – ½(0.01)
= 25.265
Class Intervals Frequency
25.265 – 25.275 3
25.275 – 25.285 15
25.285 – 25.295 19
25.295 – 25.305 24
25.305 – 25.315 29
25.315 – 25.325 21
25.325 - 25.335 6
25.335 – 25.345 3

3. Sl.no Class interval Midpoint of
class
interval(X)
Frequency
(F)
F*X F*X2
1 25.265 – 25.275 25.27 3 75.81 1915.719
2 25.275 – 25.285 25.28 15 379.2 9586.176
3 25.285 – 25.295 25.29 19 480.51 12152.1
4 25.295 – 25.305 25.3 24 607.2 15362.16
5 25.305 – 25.315 25.31 29 733.99 18577.29
6 25.315 – 25.325 25.32 21 531.72 13463.15
7 25.325 - 25.335 25.33 6 151.98 3849.653
8 25.335 – 25.345 25.34 3 76.02 1926.347
Step 6: To calculate the Mean
𝑋̅ = ∑fx / N = 3036.43 / 120
= 25.303
Step 7: To calculate the Standard deviation
S.D = √ ∑fx2
- n𝑋̅2
/ n-1 = √76832.59– 120(25.303)2
/ 119
= 0.01602497
From the graph,
The data are normally distributed
25.3425.3225.3025.28
30
25
20
15
10
5
0
C1
Frequency
Histogram of C1

4. Sl.no X1 X2 X3 X4
1 25.3 25.31 25.31 25.32
2 25.33 25.32 25.31 25.31
3 25.28 25.29 25.29 25.28
4 25.29 25.31 25.29 25.3
5 25.3 25.31 25.32 25.31
6 25.26 25.32 25.3 25.31
7 25.28 25.29 25.31 25.3
8 25.3 25.29 25.31 25.31
9 25.31 25.29 25.29 25.3
10 25.31 25.3 25.31 25.27
11 25.29 25.28 25.3 25.3
12 25.29 25.3 25.32 25.31
13 25.33 25.31 25.31 25.29
14 25.34 25.32 25.3 25.31
15 25.31 25.32 25.32 25.28
1 25.32 25.31 25.31 25.31
2 25.32 25.32 25.31 25.33
3 25.27 25.3 25.28 25.29
4 25.28 25.3 25.29 25.29
5 25.32 25.31 25.31 25.3
6 25.28 25.29 25.28 25.29
7 25.28 25.29 25.29 25.3
8 25.34 25.31 25.29 25.29
9 25.29 25.3 25.31 25.3
10 25.31 25.32 25.31 25.32
11 25.31 25.28 25.29 25.28
12 25.29 25.28 25.3 25.32
13 25.3 25.32 25.32 25.29
14 25.32 25.31 25.3 25.3
15 25.31 25.28 25.27 25.24

5. Step 1: Determine the total number of observations
N = 120
Step 2: Calculate the range of the data
Range = Maximum value – Minimum value
= 25.34- 25.24
= 0.10
Step 3: Determine the number of class intervals (k)
K = 1 + 3.33 log10(N)
= 1 + 3.33 log10(120)
= 8
Step 4: Determine the width of the class interval
Class interval = Range/K
= 0.10/8
= 0.013
Step 5: Construct the frequency distribution table
= Lowest value – ½(Least Count)
= 25.24– ½(0.01)
= 25.235
Class Intervals Frequency
25.235 – 25.248 1
25.248 – 25.261 1
25.261 – 25.274 3
25.274 – 25.287 14
25.287 – 25.30 46
25.30 – 25.31 32
25.31 - 25.32 18
25.32 – 25.34 5

6. Sl.no Class interval Midpoint of
class
interval(X)
Frequency
(F)
F*X F*X2
1 25.235 – 25.248 25.2415 1 25.2415 637.1333
2 25.248 – 25.261 25.2545 1 25.2545 637.7898
3 25.261 – 25.274 25.2675 3 75.8025 1915.34
4 25.274 – 25.287 25.2805 14 353.927 8947.452
5 25.287 – 25.30 25.2935 46 1163.501 29429.01
6 25.30 – 25.31 25.305 32 809.76 20490.98
7 25.31 - 25.32 25.315 18 455.67 11535.29
8 25.32 – 25.34 25.33 5 126.65 3208.045
Step 6: To calculate the Mean
𝑋̅ = ∑fx / N = 3035.807 / 120
= 25.29839
Step 7: To calculate the Standard deviation
S.D = √ ∑fx2
- n𝑋̅2
/ n-1 = √76801.03– 120(25.29839)2
/ 119
= 0.01448448
From the graph, the data are normally distributed and the data are skewed to the right.
25.3425.3225.3025.2825.2625.24
35
30
25
20
15
10
5
0
C2
Frequency
Histogram of C2

7. Sl.no X1 X2 X3 X4
1 25.32 25.31 25.3 25.32
2 25.31 25.32 25.28 25.31
3 25.32 25.28 25.29 25.27
4 25.3 25.31 25.3 25.29
5 25.26 25.29 25.3 25.29
6 25.3 25.3 25.31 25.33
7 25.29 25.3 25.29 25.29
8 25.3 25.31 25.31 25.31
9 25.29 25.3 25.3 25.31
10 25.25 25.31 25.3 25.3
11 25.32 25.27 25.28 25.3
12 25.27 25.26 25.28 25.31
13 25.31 25.32 25.31 25.29
14 25.3 25.3 25.29 25.3
15 25.31 25.32 25.31 25.29
1 25.29 25.32 25.31 25.32
2 25.32 25.31 25.3 25.31
3 25.33 25.32 25.32 25.34
4 25.32 25.31 25.32 25.31
5 25.32 25.29 25.29 25.32
6 25.29 25.3 25.3 25.29
7 25.26 25.32 25.3 25.28
8 25.3 25.32 25.31 25.3
9 25.29 25.33 25.28 25.31
10 25.31 25.3 25.3 25.3
11 25.31 25.31 25.33 25.32
12 25.29 25.28 25.3 25.3
13 25.3 25.31 25.32 25.32
14 25.28 25.31 25.31 25.26
15 25.29 25.3 25.3 25.31

8. Step 1: Determine the total number of observations
N = 120
Step 2: Calculate the range of the data
Range = Maximum value – Minimum value
= 25.34- 25.25
= 0.09
Step 3: Determine the number of class intervals (k)
K = 1 + 3.33 log10(N)
= 1 + 3.33 log10(120)
= 8
Step 4: Determine the width of the class interval
Class interval = Range/K
= 0.09/8
= 0.011
Step 5: Construct the frequency distribution table
= Lowest value – ½(Least Count)
= 25.25– ½(0.01)
= 25.245
Class Intervals Frequency
25.245 -25.286 1
25.286 - 25.2675 4
25.2675 - 25.2787 3
25.2787 - 25.29 27
25.29 - 25.301 30
25.301 - 25.312 29
25.312 - 25.323 21
25.323 - 25.34 5

9. Sl.no Class interval Midpoint of
class
interval(X)
Frequency
(F)
F*X F*X2
1 25.245 -25.286 25.2655 1 25.2655 638.3455
2 25.286 - 25.2675 25.27675 4 101.107 2555.656
3 25.2675 - 25.2787 25.2731 3 75.8193 1916.189
4 25.2787 - 25.29 25.28435 27 682.6775 17261.06
5 25.29 - 25.301 25.2955 30 758.865 19195.87
6 25.301 - 25.312 25.3065 29 733.8885 18572.15
7 25.312 - 25.323 25.3175 21 531.6675 13460.49
8 25.323 - 25.34 25.3315 5 126.6575 3208.424
Step 6: To calculate the Mean
𝑋̅ = ∑fx / N = 3035.948/ 120
= 25.29
Step 7: To calculate the Standard deviation
S.D = √ ∑fx2
- n𝑋̅2
/ n-1 = √76808.18– 120(25.29)2
/ 119
= 0.1849
From the graph, the data are normally distributed and the data are skewed to the right.
25.3425.3225.3025.2825.26
30
25
20
15
10
5
0
C3
Frequency
Histogram of C3