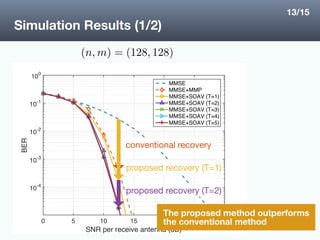
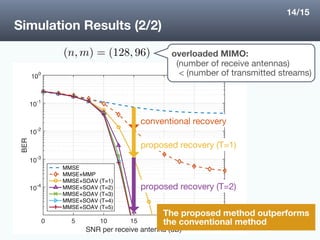
The document proposes a new error recovery method for signal detection in massive MIMO systems that improves upon conventional sparse error recovery. The proposed method estimates the error vector using relaxed MAP estimation, which takes advantage of both the sparsity and discreteness of the error vector. Simulation results show the proposed method using SOAV optimization outperforms the conventional method based on compressed sensing, achieving a lower bit error rate. The proposed method is also able to make use of soft decision values from tentative estimates rather than just hard decisions.

1. Error Recovery with Relaxed MAP Estimation
for Massive MIMO Signal Detection
Graduate School of Informatics, Kyoto University
Ryo Hayakawa and Kazunori Hayashi
The International Symposium on Information Theory and Its Applications (ISITA) 2016
October 30-November 2, 2016
Tu-B-3: Large-Scale MIMO (Organized Session)

2. Outline
❖ Introduction
❖ Conventional Sparse Error Recovery Method
❖ Proposed Error Recovery Method
❖ Simulation Results
❖ Conclusion

3. System Model of MIMO
Tx Rx
❖ transmitted signal vector:
❖ received signal vector :
❖ channel matrix :
❖ additive noise vector :
Signal Model
1/15Introduction
Assumption:
QPSK modulation

4. Conversion to Real Signal Model
Complex Model
Real Model
2/15Introduction
binary

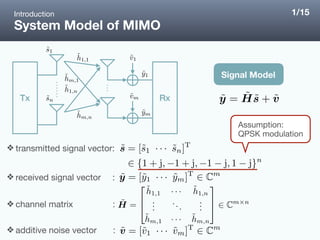
5. Signal Detection Schemes for Massive MIMO
❖ Linear detection schemes
✦ Zero forcing (ZF)
✦ Minimum mean-square-error (MMSE) etc…
❖ Nonlinear detection schemes
✦ Likelihood ascent search (LAS) [1]
✦ Reactive tabu search (RTS) [2]
✦ Gaussian belief propagation (GaBP) [3]
✦ Post-detection sparse error recovery (PDSR) [4] etc…
Introduction
Signal Detection
[1] K. V. Vardhan, et. al., “A low-complexity detector for large MIMO systems and multicarrier CDMA systems,”
IEEE J. Sel. Areas Commun., vol. 26, no. 4, pp. 473– 485, Apr. 2008.
[2] T. Datta, et. al., “Random- restart reactive tabu search algorithm for detection in large-MIMO systems,”
IEEE Commun. Lett., vol. 14, no. 12, pp. 1107–1109, Dec. 2010.
[3] T. Wo, et. al., “A simple iterative Gaussian detector for severely delay-spread MIMO channels,”
in Proc. IEEE ICC 2007, pp. 4598–4563, Jun. 2007.
[4] J.Choi, et. al., “New approach for massive MIMO detection using sparse error recovery,”
in Proc. IEEE GLOBECOM 2014, pp. 3754–3759, Dec. 2014.
3/15
estimate from

6. Signal Detection Schemes for Massive MIMO
❖ Linear detection schemes
✦ Zero forcing (ZF)
✦ Minimum mean-square-error (MMSE) etc…
❖ Nonlinear detection schemes
✦ Likelihood ascent search (LAS) [1]
✦ Reactive tabu search (RTS) [2]
✦ Gaussian belief propagation (GaBP) [3]
✦ Post-detection sparse error recovery (PDSR) [4] etc…
Introduction
Signal Detection
[1] K. V. Vardhan, et. al., “A low-complexity detector for large MIMO systems and multicarrier CDMA systems,”
IEEE J. Sel. Areas Commun., vol. 26, no. 4, pp. 473– 485, Apr. 2008.
[2] T. Datta, et. al., “Random- restart reactive tabu search algorithm for detection in large-MIMO systems,”
IEEE Commun. Lett., vol. 14, no. 12, pp. 1107–1109, Dec. 2010.
[3] T. Wo, et. al., “A simple iterative Gaussian detector for severely delay-spread MIMO channels,”
in Proc. IEEE ICC 2007, pp. 4598–4563, Jun. 2007.
[4] J.Choi, et. al., “New approach for massive MIMO detection using sparse error recovery,”
in Proc. IEEE GLOBECOM 2014, pp. 3754–3759, Dec. 2014.
improve the tentative estimate
obtained by some detection schemes
(e.g. ZF, MMSE)
3/15
estimate from

7. Outline
❖ Introduction
❖ Conventional Sparse Error Recovery Method
❖ Proposed Error Recovery Method
❖ Simulation Results
❖ Conclusion

8. Sparsity of Error Vector
error vector is sparse: most of elements are zero
Example
1. tentative
estimate
3. error
vector
sparse
Conventional Sparse Error Recovery Method
if a estimation is reliable enough
Key point
2. hard
decision
4/15
1. tentative estimate (e.g. ZF, MMSE):
2. hard decision:
3. error vector: sparse
transmitted
vector

9. 1. tentative estimate (e.g. ZF, MMSE):
2. hard decision:
3. error vector:
4. transformation into sparse system:
5. estimate of via compressed sensing:
6. corrected estimate:
Post-Detection Sparse Error Recovery (PDSR)
error vector is sparse: most of elements are zeroKey point
sparse
equation of sparse vector
Conventional Sparse Error Recovery Method 5/15

10. Outline
❖ Introduction
❖ Conventional Sparse Error Recovery Method
❖ Proposed Error Recovery Method
❖ Simulation Results
❖ Conclusion

11. 1. tentative estimate (e.g. ZF, MMSE):
2. hard decision:
3. error vector:
Discreteness of Error Vector
error vector is sparse
sparse
Example
3. error
vector
sparse
2. hard
decision
Proposed Error Recovery Method
Key point of
conventional method
Key point of
conventional method
6/15
1. tentative
estimate
transmitted
vector

12. 1. tentative estimate (e.g. ZF, MMSE):
2. hard decision:
3. error vector:
Discreteness of Error Vector
Proposed Error Recovery Method
Example
3. error
vector
sparse
+
discrete
sparse
+ discrete
2. hard
decision
Key point of
proposed method error vector is sparse and discrete-valued
6/15
1. tentative
estimate
transmitted
vector

13. estimate
via relaxed maximum a posteriori (MAP) estimation
to use both the sparsity and the discreteness
1. tentative estimate (e.g. ZF, MMSE):
2. hard decision:
3. error vector:
4. transformation into sparse system:
Proposed Error Recovery
Proposed Error Recovery Method
equation of
sparse and discrete vector
proposed method
7/15
Key point of
proposed method error vector is sparse and discrete-valued
sparse
+ discrete

14. MAP Estimation for Error Recovery
MAP estimation of
Proposed Error Recovery Method
Equation
Gaussian distribution
objective function to be minimized:
approximate as
8/15

15. objective function:
Proposed Error Recovery Method
Calculation of (1/2)
Ex. Ex.
If , then If , then
elements of :
9/15

16. Calculation of (1/2)
If , then If , then
elements of :
objective function:
Proposed Error Recovery Method
Ex. Ex.
1. calculate LLR
(with the similar approach to GaBP)
2. replace with
how to calculate this
9/15

17. Calculation of (2/2)
objective function:
norm
1.
2. ignore some terms independent of
Ex.
Proposed Error Recovery Method 10/15
For ,

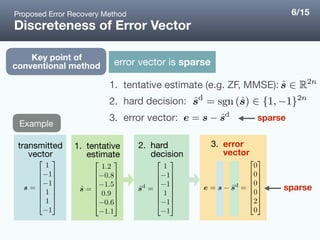
18. convex relaxation (similar to [5])
Relaxation into Convex Optimization
Combinational optimization
Convex optimization
❖ is not continuous
❖
Proposed Error Recovery Method
: Sum-of-absolute-value (SOAV) optimization [6]
[5] H. Sasahara, et. al., “Multiuser detection by MAP estimation with sum-of-absolute-values relaxation,” in Proc. IEEE ICC 2016, May 2016.
[6] M. Nagahara,“Discrete signal reconstruction by sum of absolute values,”
IEEE Signal Process. Lett., vol. 22, no. 10, pp. 1575–1579, Oct. 2015.
11/15

19. convex relaxation (similar to [5])
Relaxation into Convex Optimization
Combinational optimization
Convex optimization
❖ is not continuous
❖
Proposed Error Recovery Method
: Sum-of-absolute-value (SOAV) optimization [6]
[5] H. Sasahara, et. al., “Multiuser detection by MAP estimation with sum-of-absolute-values relaxation,” in Proc. IEEE ICC 2016, May 2016.
[6] M. Nagahara,“Discrete signal reconstruction by sum of absolute values,”
IEEE Signal Process. Lett., vol. 22, no. 10, pp. 1575–1579, Oct. 2015.
11/15
❖ is continuous
❖
If ,
then

20. Iterative Error Recovery
MMSE estimation
update of parameters
Error recovery update of
calculate LLR and update
Proposed Error Recovery Method 12/15

21. Iterative Error Recovery
MMSE estimation
update of parameters
Error recovery update of
calculate LLR and update
Proposed Error Recovery Method 12/15
recover the error of again

22. Outline
❖ Introduction
❖ Conventional Sparse Error Recovery Method
❖ Proposed Error Recovery Method
❖ Simulation Results
❖ Conclusion

23. SNR per receive antenna (dB)
0 5 10 15 20 25 30
BER
10
-4
10
-3
10
-2
10
-1
100
MMSE
MMSE+MMP
MMSE+SOAV (T=1)
MMSE+SOAV (T=2)
MMSE+SOAV (T=3)
MMSE+SOAV (T=4)
MMSE+SOAV (T=5)
Simulation Results (1/2)
conventional recovery
proposed recovery (T=1)
proposed recovery (T=2)
The proposed method outperforms
the conventional method
13/15

24. SNR per receive antenna (dB)
0 5 10 15 20 25 30
BER
10
-4
10
-3
10
-2
10
-1
100
MMSE
MMSE+MMP
MMSE+SOAV (T=1)
MMSE+SOAV (T=2)
MMSE+SOAV (T=3)
MMSE+SOAV (T=4)
MMSE+SOAV (T=5)
Simulation Results (2/2)
conventional recovery
proposed recovery (T=1)
proposed recovery (T=2)
The proposed method outperforms
the conventional method
overloaded MIMO:
(number of receive antennas)
< (number of transmitted streams)
14/15

25. Outline
❖ Introduction
❖ Conventional Sparse Error Recovery Method
❖ Proposed Error Recovery Method
❖ Simulation Results
❖ Conclusion

26. Conclusion
Conventional error recovery method
❖ estimates the error via compressed sensing
❖ uses sparsity of the error
❖ uses only hard decision of the tentative estimate
The proposed method has a better BER performance
than the conventional method
Proposed error recovery method
❖ estimates the error via SOAV optimization
❖ uses both sparsity and discreteness of the error
❖ can use soft decision of the tentative estimate
15/15