The document discusses equilibrium calculations using the equilibrium constant expression Kc. It provides examples of calculating concentrations at equilibrium using stoichiometry and initial concentrations. The examples then use the calculated equilibrium concentrations to determine the value of the equilibrium constant K for different reactions. The last example shows using the equilibrium expression to calculate the concentration of a product at equilibrium given initial concentrations and the value of K.

1. The equilibrium law
•Solve homogeneous equilibrium problems
using the expression for Kc.
–The use of quadratic equations will NOT be
assessed.

2. • In order to calculate the value of K, we
need to know the concentration in mol.dm-
3 or mol dm-3 of all reactants and products
at equilibrium.
• Sometimes we do not immediately know
all of the concentrations at equilibrium, but
we are given enough information to
determine all of the concentrations at
equilibrium and then K.

3. For Example

4. Fill this in…
Br2(g) F2(g) 2BrF(g)
Initial Conc. 0.100M 0.100M 0
Change in
conc.
Final Conc. 0.00135M

5. Should Look like:
Br2(g) F2(g) 2BrF(g)
Initial Conc. 0.100M 0.100M 0
Change in
conc.
-0.09865M -0.09865M +[2 x
0.09865M]
=0.1973M
Final Conc. 0.00135M 0.00135M 0.1973M

6. Good ol’ Stoichiometry
• We used stoichiometry (the relationship with the
balanced chemical equation to help us solve for
the final concentrations)
• Since Br2 and F2 were a 1:1 mole ratio and had
the same initial concentration, they would have
the same final.
• But BrF was a 1:2 mole ratio with Br2, so we had
to double the change in concentration and
therefore the final answer.

7. We’re not finished!
• Now we can solve for K because we found
the final concentrations (at equilibrium)
• K =[BrF]2 / [Br2][F2]
=[0.1973M]2/ [0.00135M][0.00135M]
=2.15 x 104

8. Sample Problem 2 :
A closed container initially had a CO(g)
concentration of 0.750 M and a H2O(g)
concentration of 0.275 M. It was allowed to
reach equilibrium. At equilibrium, analysis
showed a CO2(g) concentration of 0.250 M.
The equation for the reaction is:
CO(g) + H2O(g) <-->CO2(g) + H2(g)
Calculate K
Answer: K=5.00

9. SAMPLE PROBLEM 3
A closed chemical system initially contained
6.0 M SO2; 2.5 M NO2; and 1.0 M SO3.
Equilibrium was eventually reached for the
reaction
SO2(g) + NO2(g)<--> SO3(g) + NO(g)
At equilibrium, the container was found to
have 3.0 M SO3 present.
Calculate K.
Answer: K=3.00

10. • A chemist puts 0.085 mol of N2 and 0.038
mol of O2 in a 1.0 L container, once
equilibrium is reached its equilibrium
constant is found to be 4.2 x10-8. What is
the concentration of NO in the mixture at
equilibrium?
• N2(g) + O2(g) < -- > 2NO(g)

11. answer
N2(g) O2(g) ⇆ 2NO(g)
0.085 M 0.038 M 0
-x -x +2x
0.085-x 0.038-x 2x

12. Assumptions
• Normally, you would solve this using the
quadratic equation, but IB has noted that
their students will NOT need to use the
quadratic equation.
• We’re going to do a short cut that we’ll
check to make sure is okay later on.
• Instead of using 0.085-x, we’re going to
ignore the x, same for 0.038-x (ignore the
x) and solve for unknown

13. N2(g) O2(g) < -- > 2NO(g)
0.085 M 0.038 M 0
-x (ignore) -x (ignore) +2x
0.085 0.038 2x

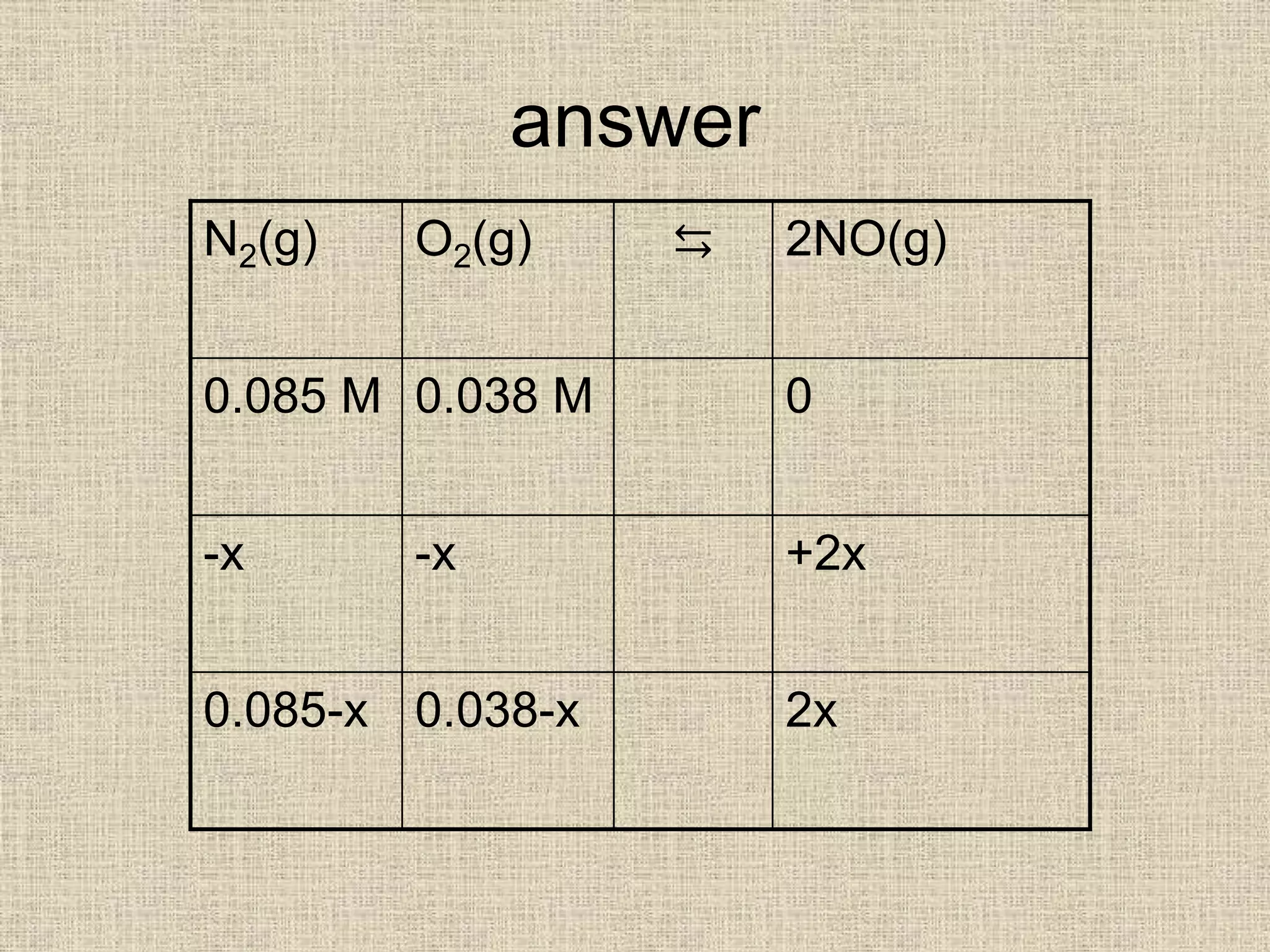
14. • k = [2x]2 =4.2 x10-8
[0.085][0.038]
4x2 = (4.2x10-8) x [0.085] x [0.038]
4x2 = 1.357 x 10-10
x2 = 3.392 x 10-11
x = 5.82 x 10-6
[NO] = 2x = 2 x 5.82 x10-6 = 1.2 x10-5 M

15. • To show that the short cut was okay,
check out your answer if the x wasn’t
omitted.
• Ex: 0.085- 5.82 x 10-6 = 0.085 (when you
only keep 2 sig figs) So it was okay to omit
the x.
• In university you won’t be so lucky!!!

16. Additional practice:

17. Using quadratic: