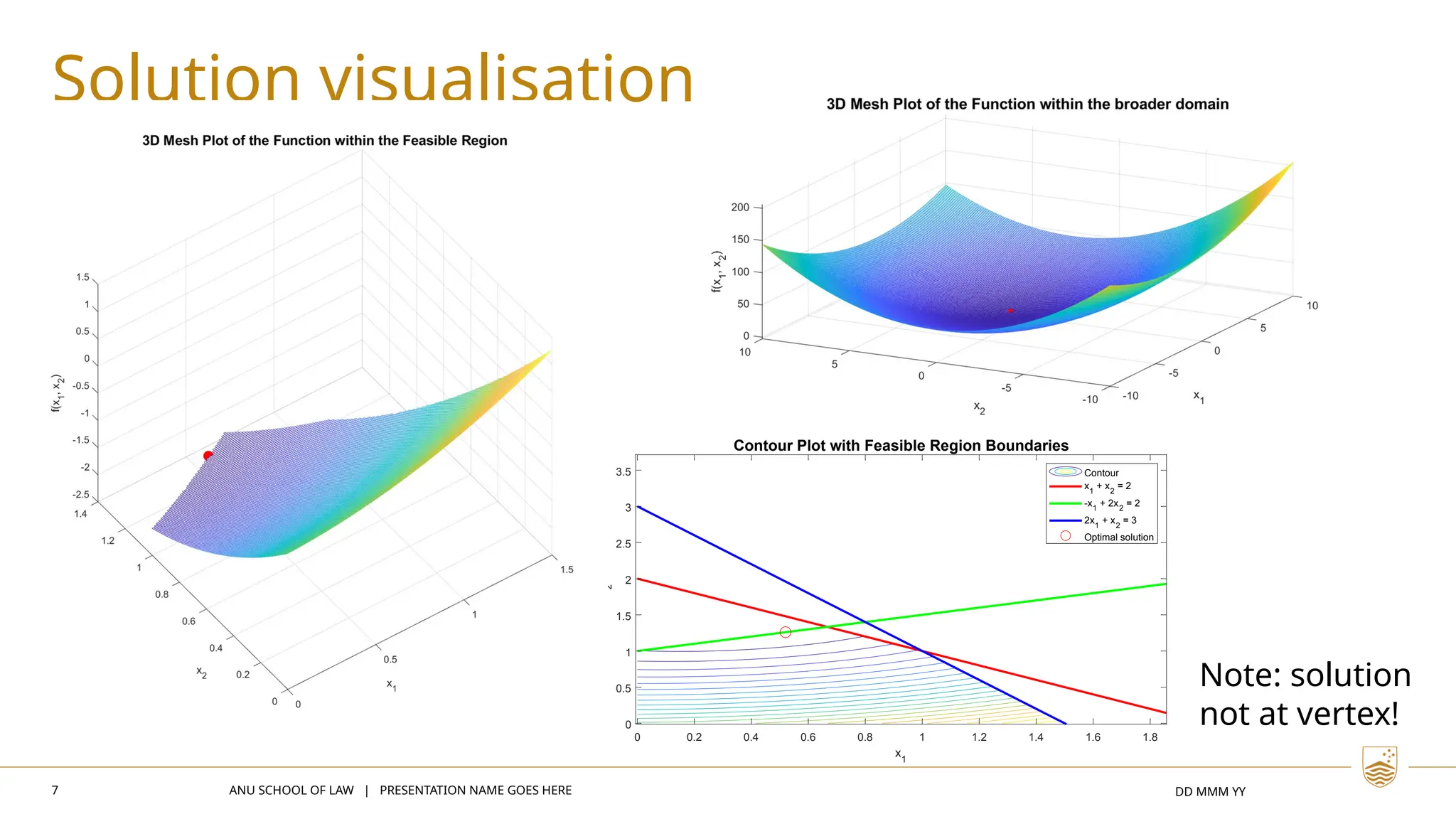
The document discusses quadratic programming as a form of non-linear programming where the objective function is quadratic and constraints are linear. It highlights the differences between linear and non-linear programming, emphasizing that optimal solutions may not occur at the vertices of the feasible region in non-linear cases. Various applications and methods for solving quadratic programming problems, including MATLAB solutions, are also presented.





![6
Matlab solution of Quadratic Problem
ANU SCHOOL OF ENGINEERING | EB4 QUADRATIC PROGRAMMING
• Minimize:
• Such that:
• Bounds
H = 2*[1/2 -1/8;
-1/8 1]; %H matrix standard form
f = [0.1; -3]; % same for f
A = [1 1;
-1 2;
2 1];
b = [2; 2; 3];
lb = zeros(2,1);
ub = [10, 10];
Aeq = [];
beq = [];
[x,fval] = quadprog(H,f,A,b,Aeq,beq,lb,ub);
x = [0.5200 1.2600] // optimal solution
𝐦𝐢𝐧
𝒙
𝟏
𝟐
𝒙
𝑻
𝑯𝒙 + 𝒇
𝑻
𝒙](https://image.slidesharecdn.com/engn3301quadraticprogramming2024-240901132345-7ebf06c9/75/ENGN3301_Quadratic_Programming_2024-pptx-6-2048.jpg)
![ANU SCHOOL OF LAW | PRESENTATION NAME GOES HERE
8 DD MMM YY
Equation to matrix form for solution
𝐦𝐢𝐧
𝒙
𝟏
𝟐
𝒙
𝑻
𝑯𝒙 + 𝒇
𝑻
𝒙
𝑧 =
1
2
𝑥1
2
+ 𝑥2
2
−
1
4
𝑥1 𝑥2 +
1
10
𝑥1 − 3 𝑥2
H = 2*[1/2 -1/8;
-1/8 1];
half of
coefficient
coefficient
for
coefficient
for
2x scaling factor as
the Matlab formulation
expects a ½ fraction in front
f = [0.1; -3];
half of
coefficient
(symmetric matrix)
coefficients for](https://image.slidesharecdn.com/engn3301quadraticprogramming2024-240901132345-7ebf06c9/75/ENGN3301_Quadratic_Programming_2024-pptx-8-2048.jpg)


