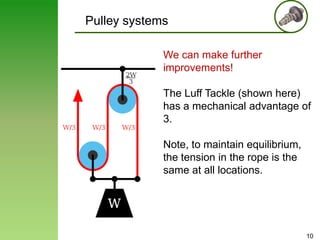
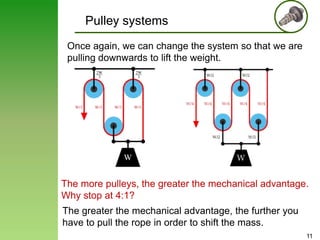
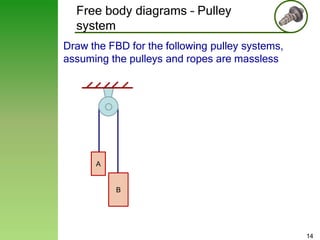
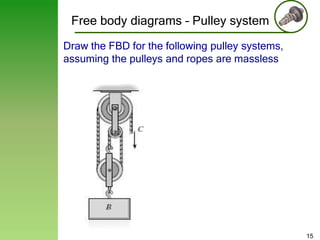
This document provides an overview of pulley systems and example problems involving pulley kinetics. It begins with examples of simple pulley systems and their free body diagrams. Equations relating the accelerations and tensions in pulley systems are developed. Two example problems are then solved in detail. They involve drawing free body diagrams, establishing equations of motion, and relating accelerations based on kinematics. The accelerations of blocks and tension in ropes are calculated for each example problem.

1. Faculty of Engineering
ENG1040
Engineering Dynamics
Pulley Systems,
Free Body Diagrams : Example Questions
Dr Lau Ee Von – Sunway
Lecture 6
ENG1040 – Engineering Dynamics

2. Past exam question
• Question 2, Sem 2, 2007
• Draw free body diagrams for Blocks A and B when
Block B is translating and accelerating downwards.
• How is acceleration of Block B related to the
acceleration of block A?
2

3. Past exam question
• How do you approach a system with several
pulleys (pulley system)?
3

4. Lecture Outline
• Pulley systems:
• How to gain mechanical leverage
• Example Questions: FBD
4

5. Pulley systems
• Pulley systems have
been used for Millennia
to reduce the force
required to lift weights.
• Employed largely in
sailing, they are
believed to have been
invented by
Archimedes (200BC).
5

6. Pulley systems
• Pulleys in everyday life:
6

7. The Simplest Pulley system
The simplest type of pulley system is
shown here.
A free-body diagram of this pulley
system shows that the total load is split
into half on either pulley rope to
maintain equilibrium.
But there must be a trade-off...
... The amount of work applied
does not change.
Energy
F d
7

8. Kinematics of Pulleys
Therefore to raise the mass a
distance d, the rope must be
hoisted a distance 2d.
This also implies that if the
rope is pulled with a velocity v,
then the mass will move with a
velocity v/2.
8

9. Further improvements
Often we want to pull down to
pull a weight up – Gun tackle
system
In this case, the beam has to
support 1½ times the weight just
to maintain equilibrium.
9

10. Pulley systems
We can make further
improvements!
The Luff Tackle (shown here)
has a mechanical advantage of
3.
Note, to maintain equilibrium,
the tension in the rope is the
same at all locations.
10

11. Pulley systems
Once again, we can change the system so that we are
pulling downwards to lift the weight.
The more pulleys, the greater the mechanical advantage.
Why stop at 4:1?
The greater the mechanical advantage, the further you
have to pull the rope in order to shift the mass.
11

12. Pulley systems
• Note: the analysis described on the previous
slides assumes that the pulleys are massless...
12

13. Kinetics/Kinematics problems...
Analysis procedure
1. Establish a coordinate system
2. Draw Free Body Diagram(s)
•
Graphical representation of all forces acting on
the system.
3. Establish known & unknown quantities
4. Apply Equation(s) of Motion in each direction
5. Evaluate kinematics to solve problem

14. Free body diagrams – Pulley
system
Draw the FBD for the following pulley systems,
assuming the pulleys and ropes are massless
A
B
14

15. Free body diagrams – Pulley system
Draw the FBD for the following pulley systems,
assuming the pulleys and ropes are massless
15

16. Free body diagrams – Pulley system
Question 2, Sem 1, 2012
Rope 2
Rope 1
C
B
F
A
16

17. Free body diagrams – Pulley system
Question 3, Sem 2, 2011

18. Kinematics
Position vector from origin
(fixed point)
Displacement = xfinal - xinitial
Equation for the
acceleration relationship
between masses
18

19. Example Question
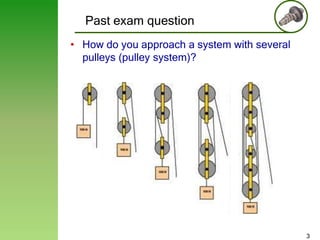
• Question 12.12 [Kinetics]
(MECHANICS FOR ENGINEERS: DYNAMICS by Ferdinand P. Beer)
The two blocks shown are originally at rest. Neglecting the
masses of the pulleys and the effect of friction in the pulleys
and between the blocks and the incline, determine
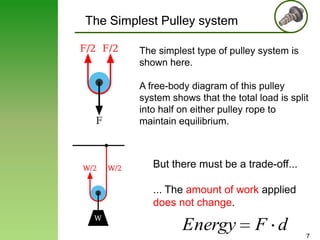
a) The acceleration of each block
b) The tension in the cable
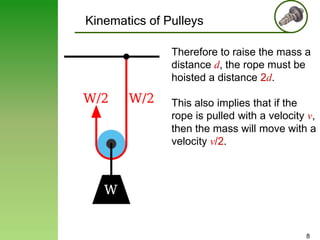
y
x
19

20. Example Question
• Question 12.12 [Kinetics]
The two blocks shown are originally at rest. Neglecting the
masses of the pulleys and the effect of friction in the pulleys
and between the blocks and the incline, determine
a) The acceleration of each block
b) The tension in the cable
y
x
20

21. Example Question
• Question 12.12 [Kinetics]
The two blocks shown are originally at rest. Neglecting the
masses of the pulleys and the effect of friction in the pulleys
and between the blocks and the incline, determine
a) The acceleration of each block
b) The tension in the cable
y
T
x
FN
mA g
Fx
T mA g sin 30o
mAaA( x)
21

22. Example Question
• Question 12.12 [Kinetics]
The two blocks shown are originally at rest. Neglecting the
masses of the pulleys and the effect of friction in the pulleys
and between the blocks and the incline, determine
a) The acceleration of each block
b) The tension in the cable
y
x
22

23. Example Question
• Question 12.12 [Kinetics]
The two blocks shown are originally at rest. Neglecting the
masses of the pulleys and the effect of friction in the pulleys
and between the blocks and the incline, determine
a) The acceleration of each block
b) The tension in the cable
3T
y
x
FN
mB g
Fx
3T mB g sin 30o
mB aB( x)
23

24. Example Question
• Question 12.12 [Kinetics]
The two blocks shown are originally at rest. Neglecting the
masses of the pulleys and the effect of friction in the pulleys
and between the blocks and the incline, determine
a) The acceleration of each block
b) The tension in the cable
o
mAaA( x)
o
mB aB( x)
T mA g sin 30
3T mB g sin 30
How many unknowns do I have?
Do I have enough equations?
24

25. Example Question
• Question 12.12 [Kinetics]
The two blocks shown are originally at rest. Neglecting the
masses of the pulleys and the effect of friction in the pulleys
and between the blocks and the incline, determine
a) The acceleration of each block
b) The tension in the cable
0
If we consider the kinematics of the
problem we can relate the
acceleration of block A with the
acceleration of block B:
x A 3x B constant
a A( x ) 3a B ( x ) 0
25

26. Example Question
• Question 12.12 [Kinetics]
The two blocks shown are originally at rest. Neglecting the
masses of the pulleys and the effect of friction in the pulleys
and between the blocks and the incline, determine
a) The acceleration of each block
b) The tension in the cable
o
mAaA( x)
o
mB aB( x)
T mA g sin 30
3T mB g sin 30
a A( x )
3a B ( x )
aA = -3.30 m/s2
aB = 1.10 m/s2
T = 16 N
26

27. Example Question
• Question 12.32 [kinetics]
The weight of blocks A, B, and C are wa = wc = 20 lb, and
wb=10 lb. Knowing that P = 50 lb and neglecting the masses
of the pulleys and the effect of friction, determine
a) The acceleration of each block
b) The tension in the cable.
1st step: Convert to SI units (see back of text book)
1 lb of force = 4.448 N of force
27

28. Example Question
• Question 12.32 [kinetics]
The weight of blocks A, B, and C are wa = wc = 20 lb, and
wb=10 lb. Knowing that P = 50 lb and neglecting the masses
of the pulleys and the effect of friction, determine
a) The acceleration of each block
b) The tension in the cable.
mAg = mCg = 88.96 N
mBg = 44.48 N
mA = mC = 9.07 kg
mB = 4.54 kg
P = 222.4 N
28

29. Example Question
• Question 12.32 [kinetics]
The weight of blocks A, B, and C are wa = wc = 20 lb, and
wb=10 lb. Knowing that P = 50 lb and neglecting the masses
of the pulleys and the effect of friction, determine
a) The acceleration of each block
b) The tension in the cable.
y
x
A
29

30. Example Question
• Question 12.32 [kinetics]
The weight of blocks A, B, and C are wa = wc = 20 lb, and
wb=10 lb. Knowing that P = 50 lb and neglecting the masses
of the pulleys and the effect of friction, determine
a) The acceleration of each block
b) The tension in the cable.
A
x
Fx
3T
mA a A( x)
30

31. Example Question
• Question 12.32 [kinetics]
The weight of blocks A, B, and C are wa = wc = 20 lb, and
wb=10 lb. Knowing that P = 50 lb and neglecting the masses
of the pulleys and the effect of friction, determine
a) The acceleration of each block
b) The tension in the cable.
B
x
Fx
2T
mB aB( x)
31

32. Example Question
• Question 12.32 [kinetics]
The weight of blocks A, B, and C are wa = wc = 20 lb, and
wb=10 lb. Knowing that P = 50 lb and neglecting the masses
of the pulleys and the effect of friction, determine
a) The acceleration of each block
b) The tension in the cable.
C
x
Fx
P 4T
mC aC ( x)
32

33. Example Question
• Question 12.32 [kinetics]
The weight of blocks A, B, and C are wa = wc = 20 lb, and
wb=10 lb. Knowing that P = 50 lb and neglecting the masses
of the pulleys and the effect of friction, determine
a) The acceleration of each block
b) The tension in the cable.
3T
m A a A( x )
2T
mB a B( x)
P
4T
mC a C ( x )
How many unknowns do I have?
Do I have enough equations?
33

34. Example Question
• Question 12.32 [kinetics]
The weight of blocks A, B, and C are wa = wc = 20 lb, and
wb=10 lb. Knowing that P = 50 lb and neglecting the masses
of the pulleys and the effect of friction, determine
a) The acceleration of each block
b) The tension in the cable.
If we consider the kinematics of the
problem we can relate the three
acceleration terms.
0
First, we note that the pulley
system is attached to the
ground at this point.
We will measure the length of
rope from this point.
34

35. Example Question
• Question 12.32 [kinetics]
The weight of blocks A, B, and C are wa = wc = 20 lb, and
wb=10 lb. Knowing that P = 50 lb and neglecting the masses
of the pulleys and the effect of friction, determine
a) The acceleration of each block
b) The tension in the cable.
If we consider the
kinematics of the
problem we can relate
the three acceleration
terms.
0
We notice that two lengths
of rope connect mass B to
the fixed point.
Therefore, part of the rope’s
length is defined as:
2 xb
This is two times the
distance from mass B to the
fixed point.
35

36. Example Question
• Question 12.32 [kinetics]
The weight of blocks A, B, and C are wa = wc = 20 lb, and
wb=10 lb. Knowing that P = 50 lb and neglecting the masses
of the pulleys and the effect of friction, determine
a) The acceleration of each block
b) The tension in the cable.
If we consider the
kinematics of the problem
we can relate the three
acceleration terms.
0
We notice that three lengths
of rope connect mass A to
the fixed point.
Therefore, part of the rope’s
length is defined as:
3 xa
This is three times the
distance from mass A to the
fixed point.
36

37. Example Question
• Question 12.32 [kinetics]
The weight of blocks A, B, and C are wa = wc = 20 lb, and
wb=10 lb. Knowing that P = 50 lb and neglecting the masses
of the pulleys and the effect of friction, determine
a) The acceleration of each block
b) The tension in the cable.
If we consider the
kinematics of the problem
we can relate the three
acceleration terms.
0
Finally, we notice that four
lengths of rope connect mass C
to the fixed point.
Therefore, part of the rope’s
length is defined as:
4 xc
This is four times the distance
from mass C to the fixed point.
37

38. Example Question
• Question 12.32 [kinetics]
The weight of blocks A, B, and C are wa = wc = 20 lb, and
wb=10 lb. Knowing that P = 50 lb and neglecting the masses
of the pulleys and the effect of friction, determine
a) The acceleration of each block
b) The tension in the cable.
I can then sum all these lengths of rope together to form:
3 xa
2 xb
4 xc
constant
From this equation, I can determine an equation for
velocity and acceleration...
38

39. Example Question
• Question 12.32 [kinetics]
The weight of blocks A, B, and C are wa = wc = 20 lb, and
wb=10 lb. Knowing that P = 50 lb and neglecting the masses
of the pulleys and the effect of friction, determine
a) The acceleration of each block
b) The tension in the cable.
First the velocity:
dxa
3
dt
dx
dt
v
3va
dxb
2
dt
2vb
dxc
4
dt
4vc
0
0
39

40. Example Question
• Question 12.32 [kinetics]
The weight of blocks A, B, and C are wa = wc = 20 lb, and
wb=10 lb. Knowing that P = 50 lb and neglecting the masses
of the pulleys and the effect of friction, determine
a) The acceleration of each block
b) The tension in the cable.
Then the acceleration:
dva
3
dt
dv
dt
a
3aa
dvb
2
dt
2ab
dvc
4
dt
4ac
0
0
I now have an equation
relating the acceleration
of the three weights.
40

41. Example Question
• Question 12.32 [kinetics]
The weight of blocks A, B, and C are wa = wc = 20 lb, and
wb=10 lb. Knowing that P = 50 lb and neglecting the masses
of the pulleys and the effect of friction, determine
a) The acceleration of each block
b) The tension in the cable.
3T
m A a A( x )
2T
Using these equations,
I can solve the problem.
Note that I have four
equations and four
unknowns.
mB a B( x)
P
3aa
4T
mC a C ( x )
2ab
4ac
0
aA = 8.9 m/s2
aB = 11.9 m/s2
aC = 12.6 m/s2
T = 27 N
41