The document proposes a hybrid approach to scalably computing pairwise comparisons of large datasets that follows a Zipf-Mandelbrot distribution. It involves pre-computing and storing the most frequent "head" comparisons while computing less frequent "body" and trivial "tail" comparisons on-demand. This balances storage and computation needs while allowing dimensionality reduction as the dataset scales. Preliminary experiments tested the approach on loan data using HBase and HDFS. Further performance testing and integration with Hadoop is suggested to prove the approach.

1. Collective Inteligence Enginering Not Bigger Research Picture (Tom) Progress Findings Proposal

2. Progress Reading.

3. Progress Investigate Compute Problem.

4. Progress Investigate Compute Problem. Pearson example.

5. Progress Investigate Compute Problem. Pearson example.

6. Progress Investigate Compute Problem. Pearson example. Store all comparisons = 1/2 N^2

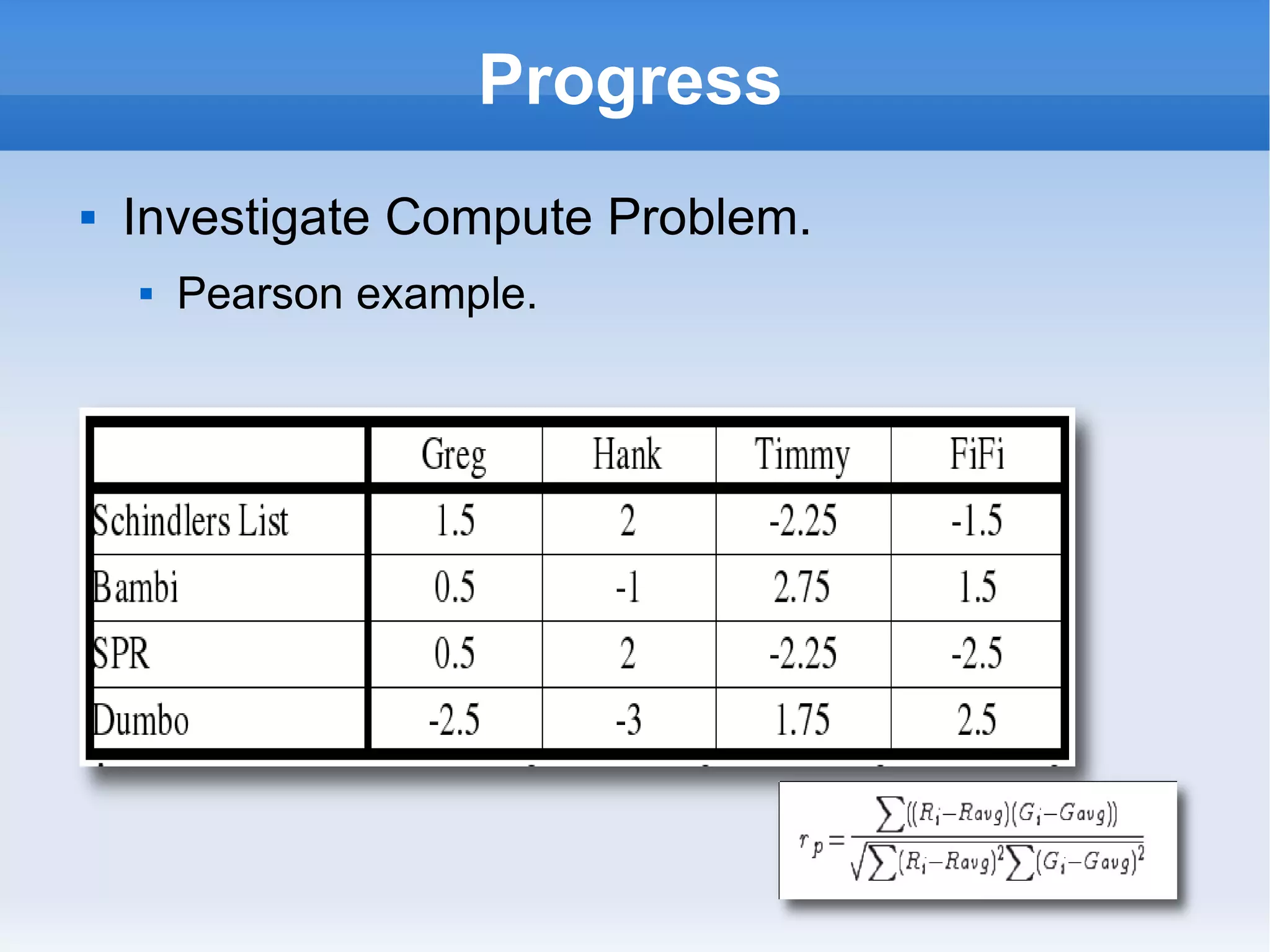
7. Progress Investigate Scale N films M people M[(N(N-1)/2] time the algorithm cost Pearson: Numerator 2 – , 1 *, 1+ Denominator 2 -, 2 ^2, 2 + M(N) time to compute averages Can be done on ingest in M(N) time

8. Progress Tractible? A typical P4 - theoretical max of 20-40 G FLOPs, With L2cach bandwidth, supporting instructions etc. a max of 3-7 G Flop is more realistic. (my further benchmarking show 7GFlop on a dual core centrino) What could we expect from various technologies Matrix multiplication is a good estimate.....

9. Progress 41 mins 17 mins 8 mins

10. Progress 40 Seconds

11. Progress Genial MFlops Which correlate well with: http://www.ient.rwth-aachen.de/~laurent/genial/benchmark_gemm_4T.html More investigation details at: http://jira.talis.com/browse/COL-5

12. Progress Computation a 1M x 1M dense matrix multiply results in at least 1M ^ 3 FLOP's = 1E18 = 1 exaflop. On a single P4 cpu this would take 1E18 / 7E9 = 142E6 seconds or 1653 days. So even on a matrix 100,000 a theoretical time of 1.65 days. Of course Comparisons are ½ this

13. Progress Realisation. Huge compute problem 1M matrix 1650 days Paralelise? 16.5 days on 100 nodes 1.65 days on 1000 nodes 10M matrix 1,650,000 days Paralelise? 16,500 days on 100 nodes 1,650 days on 1000 nodes 165 days on 10,000 nodes

14. Progress Brute force IBM's US$133M Roadrunner sustaining over 1petaflops 12,960 IBM PowerXCell 8i CPUs and 6,480 AMD Opteron dual-core processors PowerXCell 32 GFLOPS (similar to GPU's) 10M matrix = 1000 seconds (100M = 11.6 Days)

15. Progress Brute force Folding@Home (free!) is reached over 4.1 PFLOPS 10M matrix = 25 seconds ATI Radeon™ HD 4870 X2 2.4 Teraflops 500 * $500 + 250 *$1000 (each backplane) = $500,000 (£331,665) for 1 PFLOP

16. Progress Optimisations Intuitively sparse - Ignore Nulls? How sparse? True Pearson for linear algebra requires zeros, but Nulls? Depends on data – generally yes I.e three people A, B, C - A has seen no films in common with B or C A has seen 10 films, B – 5 and C – 15 Pearson numerator for B would be –15 and c -25 So C is less similar to A than B is. So can ignore nulls - tfft!

17. Progress 600 Elsevier Full Text Articles. Single core running C++ processes 20 articles / 80,000 terms per second. Computations way faster than dense matrix. Only 600 articles 150,000 unique terms. A little distraction...

18. Progress

19. Progress (from van Rijsbergen, 1979) The most frequent words are not the most descriptive More Optimisation Word Count (LSA) Characteristics Be carefull, the lower discriminatory words can provide good information... (and serendipity)

20. Progress

21. Progress How Sparse? Term Document Count from 2.18 million DBPedia Abstracts

22. Progress Distraction.... Some Least Popular (stemmed) – 3 docs each Accretionari - an increase in a beneficiary's share in an estate Accordiana - a musical radio series which was heard on CBS in 1934 Accokeek - Located in the southwest corner of Prince George's County Nazarbayev - President of Kazakhstan The Most Popular 15938 – year 12476 – season 11410 – state 10758 – world 10722 – name Serendipity

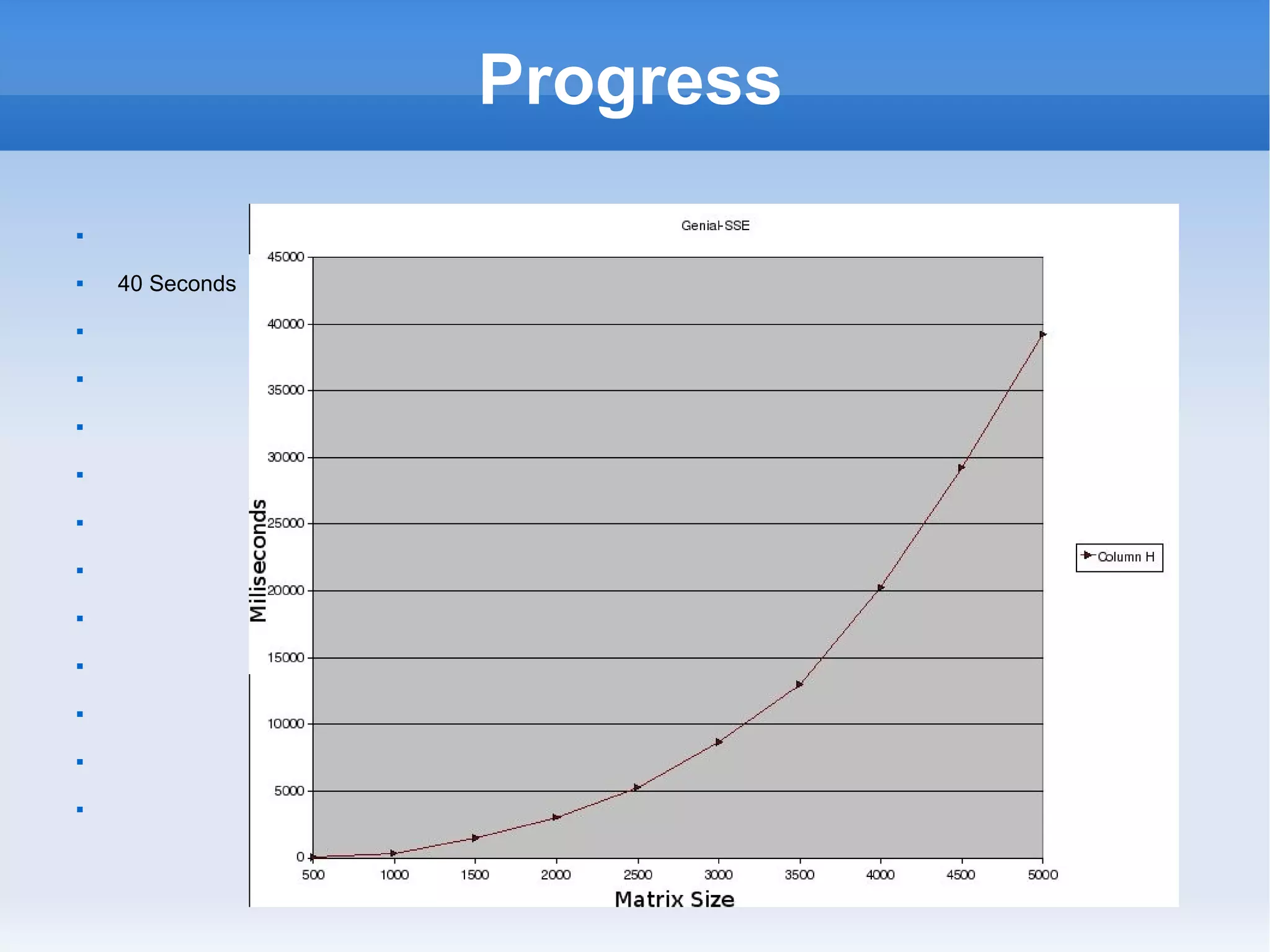
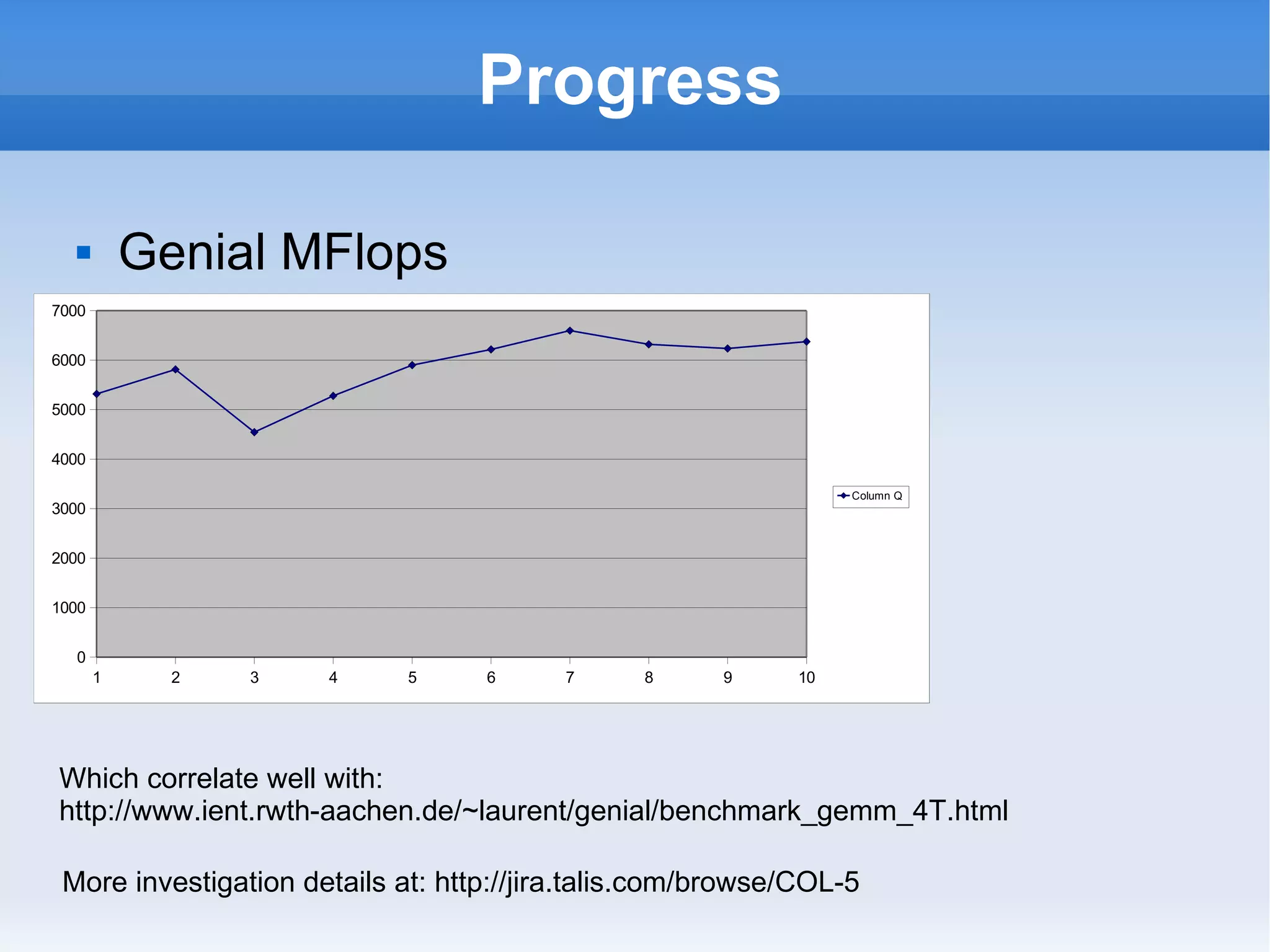
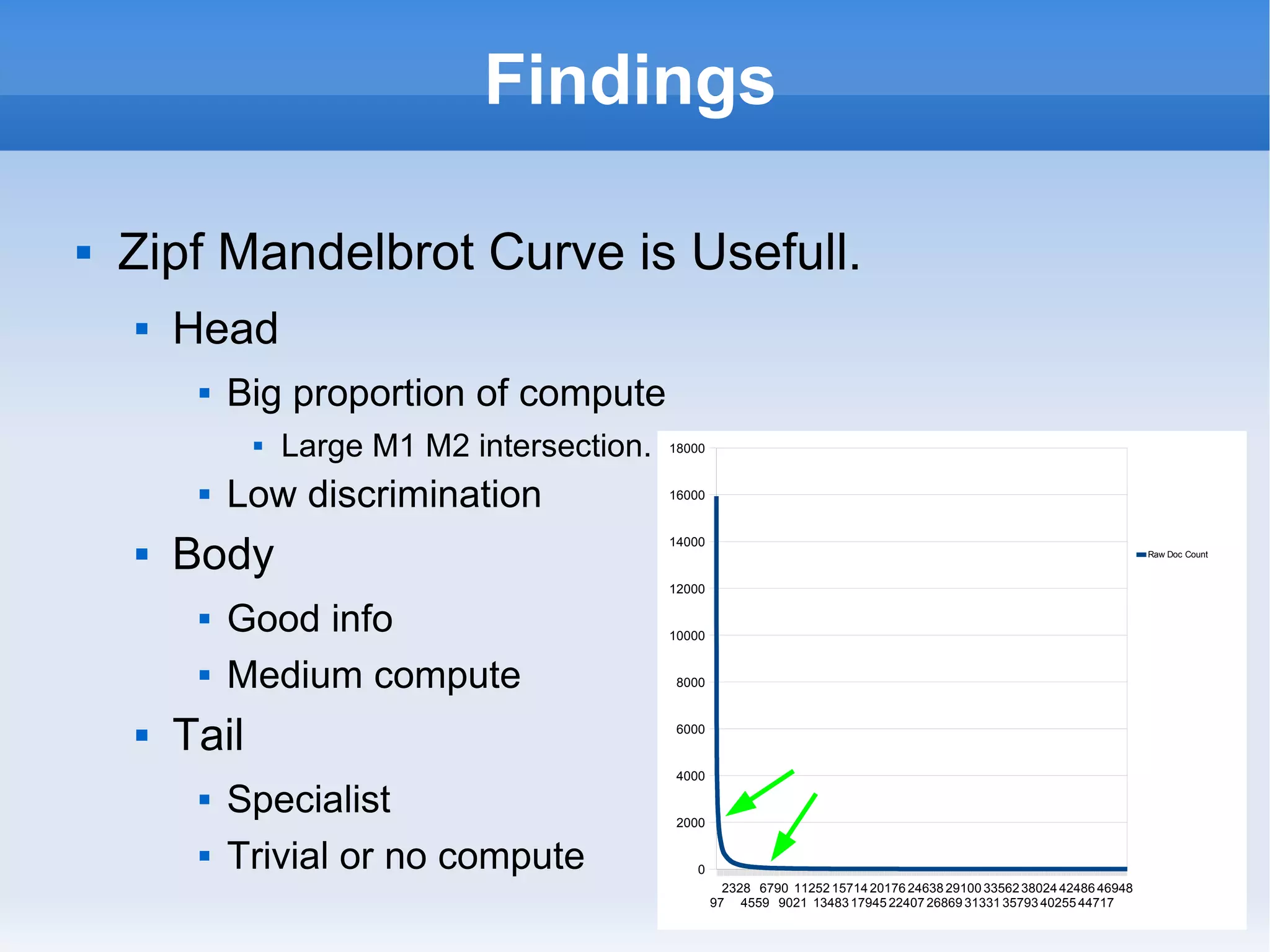
23. Progress Very Sparse Turns out to be Zipf – Mandelbrot distribution. [1] G. K. Zipf, Human Behavior and the Principle of Least Effort. (Cam- bridge, Mass., 1949; Addison-; Wesley, 1965). [2] B. Mandelbrot, “An informational theory of the statistical structure of language”, in Communication Theory, ed. Willis Jackson. (Better- worths, 1953). Word Count is .0025% dense Ignore Null for huge optimisation. 40,000 x less compute (using uniform density assumption) Zipf-Mandelbrot has the form: y = P1/(x+P2)^P3.

24. Progress DBPedia words follow Zipf-Mandelbrot Zoomed in chunk of DBPedia word count y = P1/(x+P2)^P3 best fit regression (red curve) with factors P1 = 874150 P2 = 60.0000 P3 = 1.01000

25. Progress Calculate Comparisons. 2.18 million Abstracts – 1.3M unique terms. Fits in 2G ram - (1.3M*2.18M*.000025 * 21 = 1.5G ) (as it is .0025% dense each entry is 21 bytes) Uniform density assumption Comparisons computable in few minutes Not storeable in RAM (3.6 Tbytes!) Big underestimate (Stopped the run after 4 hours) Stored random 100 article sample, and comparing with all 2M others. (0.2Gb) to allow intuitative QA

26. Progress Extrapolating Compute Times. Not 40,000x less compute (.0025% dense) Word Count is .0025% dense - 40,000 x less compute Top 1000 most commonly occurring terms the density is 0.78% Not 128x less (.78% dense) So use square of area under curve = Integral of Zipf Mandelbrot Squared Roughly a power law. y = (x^P)/N

27. Progress DBPedia Abstracs Ops (not including algorithm cost) Regression using simple power law (P = 2.1 N = 1E0.73)

28. Progress Extrapolating Compute Times. 2 Million abstracts Square of Integral of Zipf Mandelbrot Predicts calculable in 5.42 Hours Assuming all in RAM. But writing Gigs to disk big overhead. (Not run this yet to prove)

29. Progress Loans Data Ops (not including algorithm cost) (proving power law linear regression prediction) Regression using simple power law (P = 3.5 N = 1E10.15)

30. Progress Loans Data Hereford Libraries. C++ In memory 'super fast hash' Processed 19M loans in 1min 20sec. Producing 269,000 unique borrower and 491,000 unique books. 8 Million unique loan events

31. Progress Loans per Individual – Nice Zipf Mandelbrot curve

32. Progress Zipf Mandelbrot – Good Assumption? Most (all large complex systems?) data that we are likely to process will follow a Zipf-Mandlebrot model. K. Silagadze shows [1] that these comply... Clickstreams Page-rank (Linkage/Centrality) Citations Other long tail interactions. [1]Z. K. Silagadze [physics.soc-ph] 26 Jan 1999 Citations and the Zipf-Mandelbrot’s law - Budker Institute of Nuclear Physics, 630 090, Novosibirsk, Russia ing.

33. Findings Cant Store All Comparisons 50 Tb for 10M matrix (½ N^2) for triangle matrix. Store only meaningfull? – Thld = n or f. Can compute All 2M (squared) Comparisons In 6 hours (1 core). Cant Compute 1 Billion Comparisons 287 years (7 days on 20,000 cores 10Billion?). Zipf Mandelbrot Curve is Usefull. Can store All(?) raw metrics n=count - fixed f=factor - Z-M

34. Findings Zipf Mandelbrot Curve is Usefull. Head Big proportion of compute Large M1 M2 intersection. Low discrimination Body Good info Medium compute Tail Specialist Trivial or no compute

35. Findings Zipf Mandelbrot Curve is Usefull. Allows us to make optimisations In reducing the y axis (and x a bit) Chop the head off. Body Dimensionality reduction Tail Chop the tail off Or Dimensionality reduction X axis = N^2, Y axis = M

36. Findings What about storing meaningfull comparisons. Solves storage problem Requires repeated compute problem Deltas, could affect whole set Will affect a chunk of the set Could trade off timely accuracy with batch processing.

37. Proposal Store raw curve Sparse Strorage – Bigtable like Hbase, Hypertable, etc Unloads indexing and lookup to nodes. Calculate on the fly Two indeces Books -> people and People -> books Not 1/2N^2 – just 1* Intersect (* M) Tail – Retrieval problem M~0 Intersect~0. Body – Some retrieval and compute. Head – Big retrieval and compute big M big intersect.

38. Proposal Pre Compute Head Store top n Store any that take more than .5 seconds Zipf-Mandelbrot – retrieval only problem Dynamic – finding them is linear Store as a cache – only when requested? Depends on acceptible delay? This Hybrid Scales Better. Better than Storing all or Computnig all

39. Proposal It doesn't scale indefinately. * scale by 10, * nodes by 100 Dimensionality reduction will HAVE to kick in. This aproach allows that, but at bigger scles than most Consider severing head and tail as early aproach. Only optimised for individual requests. Given this article find the 10 next similar What about...”Given this corpus find the 100 most similar things” Then set n = infinity (or f=0) and the service will tell you how many days to come back for your results

40. Proposal Experimentation Used Hbase, HDFS, Hadoop Not using Hadoop yet – but is good fit for data ingest Hadoop not v efficient for comparison – but doable. Used Loan data and binary pearson Ignoring nulls (and sigma) – so counts only. Quick demo

41. Proposal Next Steps Prove this aproach Performance Testing. Hbase over n nodes (perf lab, poss then EC2?). Timing retrieval vs compute Good logging Configurable variables Multiple 'stores' (data sets). 8M loans now – 80M? Hadoop the ingest – if just to save time during trials