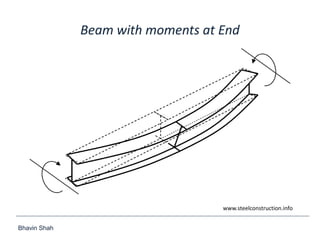
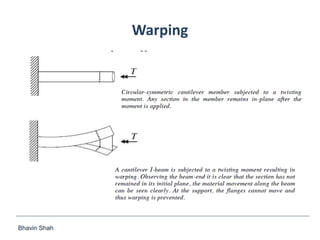
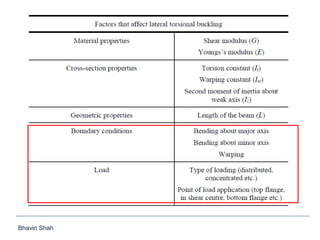
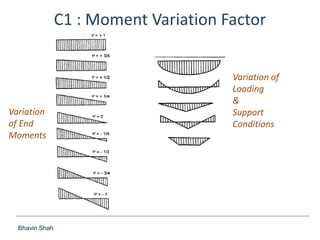
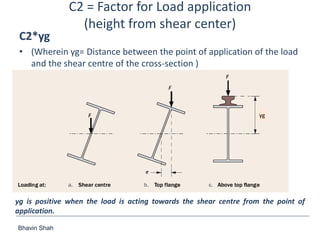
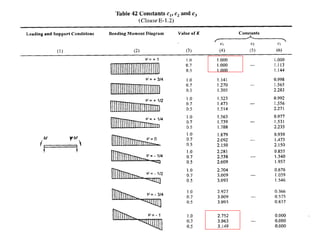
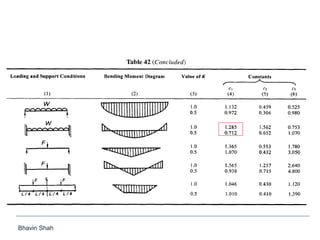
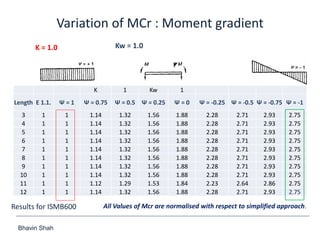
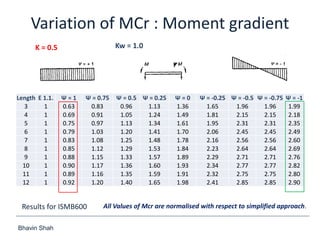
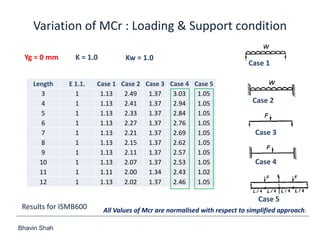
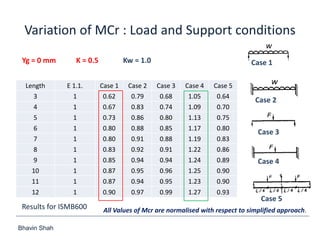
The document discusses elastic flexural-torsional buckling as a critical limit state in structural steel design, including the simplified approach outlined in IS:800-2007 and how popular software implements it. It highlights the variations in calculated elastic critical moments (Mcr) between the simplified approach and the generalised equations, emphasizing the impacts of moment variation, load height from the shear centre, and support conditions. The presentation concludes with plans to address queries related to IS:800-2007 and encourages collaboration between engineers and technical committees.

1. Elastic Flexural-Torsional
Buckling
and
IS:800-2007
Bhavin Shah
Associate Vice President
VMS Engineering & Design Services (p) ltd.

2. Content of the presentation
1. What is Elastic Flexural Torsional Buckling ?
2. IS:800-2007 (Simplified approach)
3. Approach adopted in popular software
4. Generalised equation for Mcr (Annexure-E of IS:800-
2007)
5. Comparison of results with Simplified approach and the
Generalised equation
6. Concluding Remarks
7. Way Forward

3.  What is Elastic Flexural
Torsional Buckling ?

4. Bhavin Shah
What is Elastic Flexural Torsional Buckling ?
• Flexural-torsional buckling is an important limit
state that must be considered in structural steel
design.
• Flexural-torsional buckling occurs when a
structural member experiences significant out-of-
plane bending and twisting.
• This type of failure occurs suddenly in members
with a much greater in-plane bending stiffness
than torsional or lateral bending stiffness.

5. Bhavin Shah
About US
Cantilever
Beam

6. Bhavin Shah
www.steelconstruction.info
Beam with moments at End

7. Bhavin Shah
Warping

8. Bhavin Shah

9.  IS:800-2007
(Simplified approach )

10. Bhavin Shah
C) When MCR is nearly 6 times more than (Zp * fy)

11. Bhavin Shah

12. Bhavin Shah
Effective Length

13.  Approach adopted in
the popular software

14. Bhavin Shah
• Popular software (STAAD) uses
this simplified concept for
calculating Elastic Lateral
Torsional Buckling Moment.

15. Bhavin Shah

16.  IS:800-2007
(Annexure E : Generalised equation )

17. Bhavin Shah
2
Also known as
Three factor
formulae
(depends on
C1, C2 & C3)

18. Bhavin Shah
Difference between Simplified approach
and the Generalised Equation
• Variation of moment across the span
• Height of application of load above shear
centre
• Support conditions
• Non symmetry about major axis

19. Bhavin Shah
C1 : Moment Variation Factor
Variation
of End
Moments
Variation of
Loading
&
Support
Conditions

20. Bhavin Shah
C2 = Factor for Load application
(height from shear center)
C2*yg
• (Wherein yg= Distance between the point of application of the load
and the shear centre of the cross-section )
yg is positive when the load is acting towards the shear centre from the point of
application.
yg

21. Bhavin Shah
C3 : Factor for unsymmetry about
major axis
• C3 = Applicable for sections which are not
symmetrical about major axis
• For doubly symmetric I sections, yj =0 and
hence product C3*yj = 0.
• In our subsequent discussions, we will see
effect of C1 and C2.

22. Bhavin Shah
Different boundary conditions
• K= effective length factors of the unsupported length
accounting for boundary conditions at the end lateral
supports. The effective length factor K varies from :
0.5 for complete restraint against rotation about weak
axis
1.0 for free rotate about weak axis
0.7 for the case of one end fixed and other end free.
• Kw = warping restraint Factor. Unless special
provisions to restrain warping of the section at the end
lateral supports are made, Kw should be taken as 1.0.

23. Bhavin Shah

24. Bhavin Shah

25. Bhavin Shah
Extraction of results from Dissertation carried
out by Anand Gajjar (D.D.U., Nadiad)
Guide : Bhavin Shah

26. Bhavin Shah
Variation of MCr : Moment gradient
K 1 Kw 1
Length E 1.1. Ψ = 1 Ψ = 0.75 Ψ = 0.5 Ψ = 0.25 Ψ = 0 Ψ = -0.25 Ψ = -0.5 Ψ = -0.75 Ψ = -1
3 1 1 1.14 1.32 1.56 1.88 2.28 2.71 2.93 2.75
4 1 1 1.14 1.32 1.56 1.88 2.28 2.71 2.93 2.75
5 1 1 1.14 1.32 1.56 1.88 2.28 2.71 2.93 2.75
6 1 1 1.14 1.32 1.56 1.88 2.28 2.71 2.93 2.75
7 1 1 1.14 1.32 1.56 1.88 2.28 2.71 2.93 2.75
8 1 1 1.14 1.32 1.56 1.88 2.28 2.71 2.93 2.75
9 1 1 1.14 1.32 1.56 1.88 2.28 2.71 2.93 2.75
10 1 1 1.14 1.32 1.56 1.88 2.28 2.71 2.93 2.75
11 1 1 1.12 1.29 1.53 1.84 2.23 2.64 2.86 2.75
12 1 1 1.14 1.32 1.56 1.88 2.28 2.71 2.93 2.75
K = 1.0 Kw = 1.0
Results for ISMB600 All Values of Mcr are normalised with respect to simplified approach.

27. Bhavin Shah
Variation of MCr : Moment gradient
Length E 1.1. Ψ = 1 Ψ = 0.75 Ψ = 0.5 Ψ = 0.25 Ψ = 0 Ψ = -0.25 Ψ = -0.5 Ψ = -0.75 Ψ = -1
3 1 0.63 0.83 0.96 1.13 1.36 1.65 1.96 1.96 1.99
4 1 0.69 0.91 1.05 1.24 1.49 1.81 2.15 2.15 2.18
5 1 0.75 0.97 1.13 1.34 1.61 1.95 2.31 2.31 2.35
6 1 0.79 1.03 1.20 1.41 1.70 2.06 2.45 2.45 2.49
7 1 0.83 1.08 1.25 1.48 1.78 2.16 2.56 2.56 2.60
8 1 0.85 1.12 1.29 1.53 1.84 2.23 2.64 2.64 2.69
9 1 0.88 1.15 1.33 1.57 1.89 2.29 2.71 2.71 2.76
10 1 0.90 1.17 1.36 1.60 1.93 2.34 2.77 2.77 2.82
11 1 0.89 1.16 1.35 1.59 1.91 2.32 2.75 2.75 2.80
12 1 0.92 1.20 1.40 1.65 1.98 2.41 2.85 2.85 2.90
K = 0.5 Kw = 1.0
Results for ISMB600 All Values of Mcr are normalised with respect to simplified approach.

28. Bhavin Shah
Variation of MCr : Loading & Support condition
Length E 1.1. Case 1 Case 2 Case 3 Case 4 Case 5
3 1 1.13 2.49 1.37 3.03 1.05
4 1 1.13 2.41 1.37 2.94 1.05
5 1 1.13 2.33 1.37 2.84 1.05
6 1 1.13 2.27 1.37 2.76 1.05
7 1 1.13 2.21 1.37 2.69 1.05
8 1 1.13 2.15 1.37 2.62 1.05
9 1 1.13 2.11 1.37 2.57 1.05
10 1 1.13 2.07 1.37 2.53 1.05
11 1 1.11 2.00 1.34 2.43 1.02
12 1 1.13 2.02 1.37 2.46 1.05
Case 1
Case 2
Case 3
Case 4
Case 5
Yg = 0 mm K = 1.0 Kw = 1.0
Results for ISMB600 All Values of Mcr are normalised with respect to simplified approach.

29. Bhavin Shah
Variation of MCr : Load and Support conditions
Length E 1.1. Case 1 Case 2 Case 3 Case 4 Case 5
3 1 0.75 0.74 0.84 1.08 0.71
4 1 0.77 0.74 0.86 1.08 0.73
5 1 0.79 0.75 0.89 1.08 0.75
6 1 0.81 0.76 0.92 1.09 0.77
7 1 0.84 0.77 0.95 1.11 0.79
8 1 0.85 0.79 0.97 1.12 0.80
9 1 0.87 0.81 1.00 1.15 0.82
10 1 0.89 0.83 1.02 1.17 0.83
11 1 0.88 0.83 1.02 1.17 0.83
12 1 0.92 0.87 1.06 1.22 0.86
Yg = 300mm K = 1.0 Kw = 1.0
Results for ISMB600
Case 1
Case 2
Case 3
Case 4
Case 5
All Values of Mcr are normalised with respect to simplified approach.

30. Bhavin Shah
Variation of MCr : Load and Support conditions
Length E 1.1. Case 1 Case 2 Case 3 Case 4 Case 5
3 1 0.40 0.31 0.37 0.38 0.36
4 1 0.47 0.35 0.44 0.43 0.43
5 1 0.53 0.39 0.51 0.48 0.49
6 1 0.58 0.43 0.57 0.53 0.55
7 1 0.63 0.47 0.63 0.59 0.60
8 1 0.67 0.51 0.67 0.63 0.64
9 1 0.70 0.54 0.71 0.68 0.68
10 1 0.73 0.57 0.74 0.72 0.71
11 1 0.73 0.58 0.75 0.74 0.72
12 1 0.77 0.62 0.80 0.79 0.76
Results for ISMB600
Yg = 300mm K = 0.5 Kw = 1.0 Case 1
Case 2
Case 3
Case 4
Case 5
All Values of Mcr are normalised with respect to simplified approach.

31. Bhavin Shah
Variation of MCr : Load and Support conditions
Length E 1.1. Case 1 Case 2 Case 3 Case 4 Case 5
3 1 0.62 0.79 0.68 1.05 0.64
4 1 0.67 0.83 0.74 1.09 0.70
5 1 0.73 0.86 0.80 1.13 0.75
6 1 0.80 0.88 0.85 1.17 0.80
7 1 0.80 0.91 0.88 1.19 0.83
8 1 0.83 0.92 0.91 1.22 0.86
9 1 0.85 0.94 0.94 1.24 0.89
10 1 0.87 0.95 0.96 1.25 0.90
11 1 0.87 0.94 0.95 1.23 0.90
12 1 0.90 0.97 0.99 1.27 0.93
Results for ISMB600
Yg = 0 mm K = 0.5 Kw = 1.0 Case 1
Case 2
Case 3
Case 4
Case 5
All Values of Mcr are normalised with respect to simplified approach.

32. Bhavin Shah
Concluding Remarks
 Flexural-torsional buckling is an important limit state
that must be considered in structural steel design.
 Popular software adopts simplified approach for
calculation of elastic critical moment (Mcr).
 In the simplified approach, effect of moment variation
across the span, height of loading from shear centre
and different supporting conditions are not
considered.
 There can be substantial variation in the value of Mcr
(between simplified vs generalised equation as per
Annexure-E of IS:800-2007).

33. Bhavin Shah
Way Forward
 As a part of the road map of IAStructE for 2014-16, it has
been decided to form the separate professional committee,
named as BIS-CODAL Committee, IAStructE.
 Main aim of the committee shall be to bridge the gap between
practicing engineers / academicians and BIS Technical
Committee (CED). For details of the committee, pl visit
: http://iaseguj.org/forum/topic/33
 We have initiated the activities with IS:800-2007. All the
collated queries / comments (received from across the
country) will be sent to BIS for further action.
 You may send your queries related to IS:800-2007 vide e-mail
: bis.iastructe@gmail.com

34. Bhavin Shah
References :
• IS:800-2007 – General construction in steel
• A Parametric Study of Elastic Critical Moments in StructuralDesign
Software by MARTIN AHNLÉN JONAS WESTLUND
• Lateral-Torsional Buckling of Steel Beams with Open Cross
Section by HERMANN ÞÓR HAUKSSON JÓN BJÖRN
VILHJÁLMSSON
• Stability of Steel beams and columns by TATA Steel

35. Bhavin Shah
Thank You….!!!
Bhavin Shah
Email : bhavin@vmsconsultants.com
Cell no. : +91 9428765878