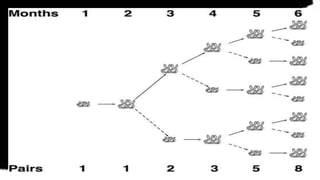
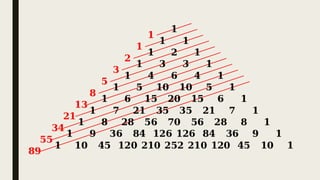
The document discusses the Fibonacci sequence and its applications, highlighting the Fibonacci problem related to rabbit reproduction. It also covers key mathematical developments, including the separation of trigonometry from astronomy, and the contributions of mathematicians like Luca Pacioli and John Napier. Furthermore, it touches on Newton's Principia Mathematica and its foundational role in understanding celestial motions through mathematics.

2. (c. 1170 – c. 1250)
• Fibonacci Problem(1202)
• Book: Liber Abaci
• “Fibonacci Sequence”
• use of the Hindu-Arabic numeral
system throughout Europe

3. FIBONACCI SEQUENCE
Reproduction of rabbits

4. The Fibonacci Problem:
Suppose there are two newborn rabbits, one
male and the other female. Find the number of
rabbits produced in a year if:
 Each pair takes one month to become mature:
 Each pair produces a mixed pair every month,
from the second month; and
 All rabbits are immortal.

6. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
FIBONACCI
SEQUENCE
Any Fibonacci number, except the first
two, is the sum of the two immediately
preceding Fibonacci numbers.

7. They occur in nature, music,
geography, and geometry.

8. Fibonacci and Pascal’s Triangle

9. Fibonacci numbers
can be extracted
from Pascal’s
triangle.

11. • explanation of the Hindu- Arabic
numerals & exponential
notations.

12. (15th Century)
• He helped separate trigonometry
from astronomy
• through his efforts trigonometry
came to be considered an
independent branch of mathematics.
• "De Triangulis“ the first great book on
trigonometry

13. (1445-1514)
• Rediscovery of Greek Geometry
• a Franciscan friar and mathematician
• stands at a table filled with geometrical tools (slate, chalk,
compass, dodecahedron model, etc.), illustrating a theorem
from Euclid, while examining a beautiful glass
rhombicuboctahedron half- filled with water.

14. Luca Pacioli’s
Summa
• Arithmetic- devices for
multiplication and forfinding
roots
• Algebra- standard solution on linear
& quadraticequations

15. Leonardo Da Vinci and Luca Pacioli

16. Pacioli and Leonardo DaVinci
Luca Pacioli's 1509 book The Divine Proportion was
illustrated by Leonardo Da Vinci.
Shown here is a drawing of an icosidodecahedron and an
"elevated" form of it. For the elevated forms, each face is
augmented with a pyramid composed of equilateral triangles.

17. ( 1540-1603 )
• Viete and Symbolic Algebra
• In Artem Analyticam Isagoge (Introduction to
the Analytic Art, published in1591)
• He demonstrated the value of symbols.
• He suggested using letters as symbols for
quantities, both known and unknown.

18. In his Mirifici Logarithmorum Canonis descriptio
(1614) the Scottish nobleman John Napier
introduced the concept of logarithms as an aid
to calculation.
( 1550-1617 )

19. Kepler’s first attempt to describe planetary
orbits used a model of nested regular
polyhedra (Platonic solids).
( 1571-1630 )

20. Newton’s Principia Mathematica (1687) presented, in
the style of Euclid’s Elements, a mathematical theory
for celestial motions due to the force of gravity. The
laws of Kepler were “proved” in the sense that they
followed logically from a set of basic postulates.
1642 - 1727

21. THANK
YOU!