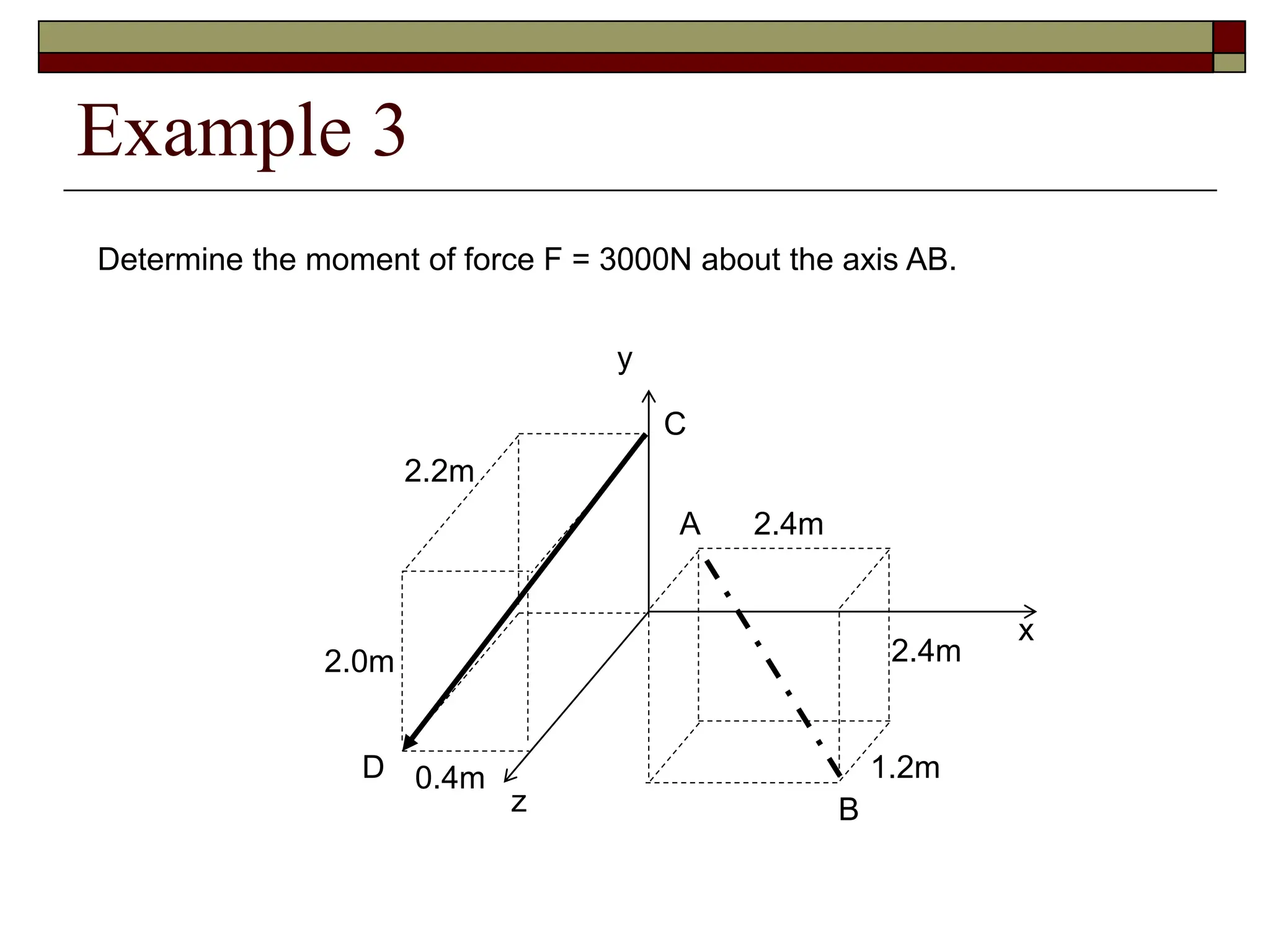
1. The document discusses moments of forces about points and axes in 3D space. It defines the moment of a force about a point as the cross product of the position vector and the force vector. 2. An example problem is presented to calculate the moment of a 3000N force about a point. The shortest distance between the point and the line of action of the force is also determined. 3. The moment of the same 3000N force about the axis between two points is then calculated. Dot and cross products of vectors are used to solve for the moments.

1. Lecture 5 – Rigid bodies: Moment 3D
What you will learn for today?
1. Moment of a force about a point in 3D
2. Moment of a force about an axis in 3D
• Angle between two vectors
• Nearest distance between two vectors
3. Example and exercise
By: Ts. Dr. Muhammad Hanif Ramlee
Credit to: Prof. Dato’ Ir. Dr. Mohammed Rafiq Abdul Kadir

2. Moment of a force about a point (3D)
Vector identity:
Cross Product (×)
Q

P
P
Q
Q
P
PQ
P
Q
PQ
Q
P










sin
sin
RIGHT HAND RULE
{ + k }
{ - k }

3. Moment of a force about a point (3D)
Definition of Moment about a point
F
r
M 
 where r = position vector
Start – the point where moment is taken
End – the point where the force acts
k
F
j
F
i
F
F
k
r
j
r
i
r
r
z
y
x
z
y
x






   
k
F
j
F
i
F
k
r
j
r
i
r
M z
y
x
z
y
x 






4. Moment of a force about a point (3D)
In 3D analysis, r and F are resolved into x, y, and z components.
sin  = 0 or 1
j
k
i
k
j
i
i
i






 0
i
k
j
j
j
k
i
j







0
0







k
k
i
j
k
j
i
k
           
     k
F
r
F
r
j
F
r
F
r
i
F
r
F
r
M
i
F
r
j
F
r
i
F
r
k
F
r
j
F
r
k
F
r
M
x
y
y
x
z
x
x
z
y
z
z
y
y
z
x
z
z
y
x
y
z
x
y
x













5. Moment of a force about a point (3D)
The equation can also be solved using determinant
x
x
F
r
i
y
y
F
r
j
z
z
F
r
k
           
     k
F
r
F
r
j
F
r
F
r
i
F
r
F
r
M
j
F
r
i
F
r
k
F
r
k
F
r
j
F
r
i
F
r
M
x
y
y
x
z
x
x
z
y
z
z
y
z
x
y
z
x
y
y
x
x
z
z
y












x
x
F
r
i
y
y
F
r
j

6. Example 1
b) Determine the shortest distance between point A and line of action of the force
a) Determine the moment of force F = 3000N about a point A.
x
y
z
D
2.2m
2.0m
0.4m
O
C
A
1.2m

7. Example 1
Nk
Nj
Ni
F
k
j
i
F
k
d
d
j
d
d
i
d
d
F
F
F
F
CD
CD
z
y
x
CD
CD
CD
CD
CD
2200
2000
400
3
2
.
2
3
0
.
2
3
4
.
0
3000


























 
Solutions for (a)
x
y
z
D
2.2m
2.0m
0.4m
O
C
A
1.2m
CD
AD
CD
AC
A F
r
F
r
M 




8. Example 1
   
       
       
Nmk
Nmj
Nmi
M
Nmi
Nmj
Nmi
Nmk
M
i
N
m
j
N
m
i
N
m
k
N
m
M
Nk
Nj
Ni
mk
mj
M
F
r
M
A
A
A
A
CD
AC
A
800
480
6800
2400
480
4400
800
2000
2
.
1
400
2
.
1
2200
0
.
2
400
0
.
2
2200
2000
400
2
.
1
0
.
2























r can be chosen from either rAC or rAD.
mk
mi
r
mk
mj
r
AD
AC
4
.
3
4
.
0
2
.
1
0
.
2





lets choose rAC

9. Example 1
 
m
F
M
d
Nm
M
M
M
M
M
M
F
M
d
d
F
M
A
A
A
z
y
x
A
A
A
288
.
2
3000
7
.
6863
7
.
6863
800
480
6800 2
2
2
2
2
2















Solutions for (b)

10. Moment of a force about a point (3D)
Vector identity:
Dot Product (·), is a scalar.
Q

P
P
Q
Q
P
PQ
P
Q
PQ
Q
P










cos
cos
Direction
not
associated

11. Moment of a force about a point (3D)
In 3D analysis, vectors are resolved into x, y, and z components.
cos  = 1 or 0
0
0
1






k
i
j
i
i
i
0
1
0






k
j
j
j
i
j
1
0
0






k
k
j
k
i
k

12. Moment of a force about a point (3D)
The dot product is used to determine:
The angle between two vectors
The moment of a force about an axis
The perpendicular / 90° / nearest distance between two
vectors (the line of action)

13. The angle between two vectors
    
cos
PQ
k
Q
j
Q
i
Q
k
P
j
P
i
P z
y
x
z
y
x 






cos
PQ
Q
P 

k
Q
j
Q
i
Q
Q
k
P
j
P
i
P
P
z
y
x
z
y
x






Q

P
2
2
2
z
y
x P
P
P
P 


2
2
2
z
y
x Q
Q
Q
Q 


  
cos
PQ
Q
P
Q
P
Q
P z
z
y
y
x
x 


 
PQ
Q
P
Q
P
Q
P z
z
y
y
x
x 


 
cos

14. Example 2
Determine the angle between vectors P = 6i +6j – 7k and Q = -6i +33j -30k
 
PQ
Q
P
Q
P
Q
P z
z
y
y
x
x 



cos
         372
30
7
33
6
6
6 







 z
z
y
y
x
x Q
P
Q
P
Q
P
  11
7
6
6
2
2
2
2
2
2







 z
y
x P
P
P
P
    45
30
33
6
2
2
2
2
2
2








 z
y
x Q
Q
Q
Q
  

38
.
41
7515
.
0
45
11
372
cos






15. Moment of a force about an axis
B
AB
AB
A
AB
AB
M
M
or
M
M






int
po
axis
axis M
M 
 
definition
application
where
MAB = moment of force F about axis AB
AB = unit vector from A to B
MA or MB = moment of force F about point A or point B

16. Example 3
Determine the moment of force F = 3000N about the axis AB.
x
y
z
2.2m
2.0m
0.4m
2.4m
2.4m
1.2m
C
D
A
B

17. Example 3
A
AB
AB M
M 
  B
AB
AB M
M 
 
int
po
axis
axis M
M 
 
Solution
       
CD
BD
AB
CD
BC
AB
CD
AD
AB
CD
AC
AB
AB F
r
F
r
F
r
F
r
M 










 



Observe that AB and FCD are common to all equations, the difference lies in the
position vector, r. Unless otherwise stated, it is advisable to choose the ‘simplest’ r.

18. Example 3
Solution
k
j
i
k
j
i
k
d
d
j
d
d
i
d
d
k
j
i
Z
Y
X
ABz
ABy
ABx
AB

































 














3
1
3
2
3
2
6
.
3
2
.
1
6
.
3
4
.
2
6
.
3
4
.
2





19. Example 3
Solution
Nk
Nj
Ni
F
k
j
i
F
k
d
d
j
d
d
i
d
d
F
F
F
F
Z
Y
X
CD
CD
CD
2200
2000
400
3
2
.
2
3
0
.
2
3
4
.
0
3000






















 






 










 

20. Example 3
Solution
mk
mj
mi
r
mj
mi
r
mk
mi
r
mk
mj
r
BD
BC
AD
AC
2
.
2
4
.
2
8
.
2
4
.
4
4
.
2
4
.
3
4
.
0
2
.
1
0
.
2













21. Example 3
 
CD
AC
axis
axis F
r
M 

 
Solution
   
 
   
   
   
   
 
 
Nm
Nmk
Nmj
Nmi
k
j
i
Nmi
Nmj
Nmi
Nmk
k
j
i
i
N
m
j
N
m
i
N
m
k
N
m
k
j
i
Nk
Nj
Ni
mk
mj
k
j
i
5120
3
800
3
960
3
13600
800
480
6800
3
1
3
2
3
2
2400
480
4400
800
3
1
3
2
3
2
2000
2
.
1
400
2
.
1
2200
0
.
2
400
0
.
2
3
1
3
2
3
2
2200
2000
400
2
.
1
0
.
2
3
1
3
2
3
2



















































































22. Nearest distance between two vectors
2
2
parallel
lar
Perpendicu F
F
F 

d
F
M lar
Perpendicu
axis 
F
F AB
parallel 
 
The component of a vector (F) that is parallel to an axis (AB) is given by
The perpendicular component of the vector is
From the definition of moment about an axis
Where d = perpendicular distance
lar
Perpendicu
axis
F
M
d 


23. Example 4
Determine the shortest distance between the line of action of force
F = -400Ni – 2000Nj +2200Nk and the line AB.
x
y
z
2.2m
2.0m
0.4m
2.4m
2.4m
1.2m
C
D
A
B

24. Example 4
Nm
M
M AB
axis 5120


 
     
m
F
M
d
N
F
N
N
N
N
Nk
Nj
Ni
k
j
i
F
F
F
F
F
lar
perpendicu
axis
lar
perpendicu
AB
parallel
parallel
lar
Perpendicu
133
.
2
2400
5120
2400
3
5400
3000
3
5400
2200
3
1
2000
3
2
400
3
2
2200
2000
400
3
1
3
2
3
2
2
2
2
2










































Solution
N
F 3000


25. Exercise 1
x
y
z
0.15m
0.25m
0.1m
A
B
O
F=150N
0.3m
C
Determine the moment of the F = 150N force about the diagonal BA.
Answer:
MAB = 14.52 Nm