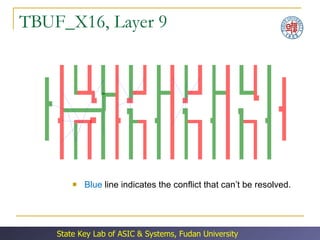
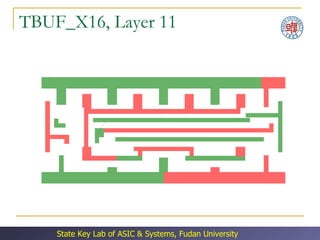
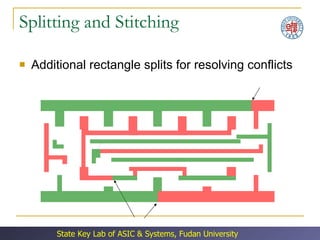
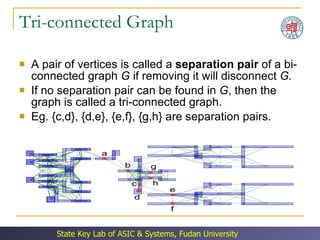
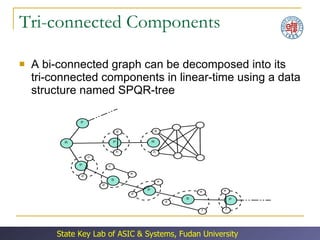
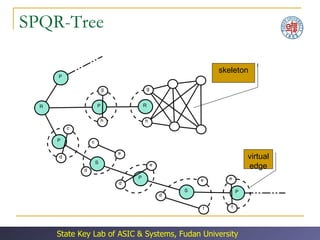
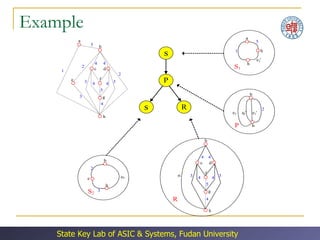
The document discusses double patterning lithography (DPL) as a technique to overcome limitations of optical lithography at smaller feature sizes. It presents an algorithm for DPL layout splitting that involves: (1) decomposing the conflict graph into tri-connected components, (2) solving each component independently, and (3) merging the solutions. Experimental results showed the algorithm achieved a 3-10x speedup over previous approaches.

1. Double Patterning Wai-Shing Luk

2. Background At the past, chips were continuously getting smaller and smaller, and hence less power consumption. However, we’re fast approaching the end of the road where optical lithography( 光刻 ) cannot take us where we need to go next.

3. 光刻过程 Photo-resist coating Illumination Exposure Etching Impurities Doping Metal connection

4. Sub-wavelength Lithograph Feature size << lithograph wavelength 45nm vs. 193nm What you see in the mask/layout is not what you get in the chip: 图形失真 成品率下降

5. What is Double Patterning? Instead of exposing the photo-resist layer once under one mask, as in conventional optical lithography, expose it twice, by splitting the mask into two, each with features half as dense.

6. TBUF_X16, Layer 9 Blue line indicates the conflict that can’t be resolved.

7. TBUF_X16, Layer 11

8. SDFFRS_X2 Layer 9, 11

9. 45nm Example

10. Random, 4K rectangles

11. fft_all.gds, 320K polygons

12. Current Status of Our SW fft_all: 320K polygons, 1.3M rectangles Conflict graph construction within 1 minute Color assignment within 9 minutes Compare: 26 minutes for just displaying the result using “eog” Note: Only g++ 3.4.5 was used, no advanced compiler optimization has been done yet.

13. Key Techniques Novel polygon cutting algorithm to reduce the number of rectangles and the total cut-length. Novel dynamic priority search tree for plane-sweeping. Decompose the underlying conflict graph into its tri-connected components using SPQR-tree Graph-theoretical approach instead of ILP Recast the coloring problem as a T-join problem and is then by solved by Hadlock’s algorithm

14. New Polygon Cutting Algorithm Allow minimal overlapping to reduce the number of rectangles, and hence to reduce the number of conflicts. Limited support of diagonal line segments

15. Dynamic Priority Search Tree In plane sweeping, events are frequently “inserted” and “deleted” to the scan line. In our PST, all data are stored at the leaf nodes of PST, making “insert” and “delete” operations very fast (O(1) time for each tree rotation). The payoff is that the “query” operation will be little slower than the traditional PST.

16. Splitting and Stitching Additional rectangle splits for resolving conflicts

17. Conflict Detection Two rectangles are NOT conflict if their distance is > b. Conflict: (A,C), (A,E), (E,B), (B,D), but not (A,B), (A,D) (B,C)! Define: a polygon is said to be rectilinearly convex if it is both x-monotone and y-monotone. Rule: (A,D) are not conflict because A-F-D reconstructs a rectilinearly convex polygon. (A,C) are conflict because A-F-C reconstructs a rectilinearly concave polygon A B C D E F b

18. Layout Splitting Problem Formulation INSTANCE: Graph G = ( V , E ) and a weight function w : E  N SOLUTION: Disjoint vertex subsets V 0 and V 1 where V = V 0 ∪ V 1 MINIMIZE: the total cost of edges whose end vertices in same color. Note: the problem is linear-time solvable for bipartite graphs, polynomial-time solvable for planar graphs, but NP-hard in general. To reduce the problem size, graph partitioning techniques could be used.

19. Bi-connected Graph A vertex is called a cut-vertex of G if removing it will disconnect G. If no cut-vertex can be found in G , then the graph is called a bi-connected graph. For example, a and b below are cut-vertices.

20. Bi-connected Components A connected graph can be decomposed into its bi-connected components in linear-time. Each bi-connected component can be solved independently without affecting the final sol’n. Question: Is it possible to further decompose the graph?

21. Tri-connected Graph A pair of vertices is called a separation pair of a bi-connected graph G if removing it will disconnect G. If no separation pair can be found in G , then the graph is called a tri-connected graph. Eg. {c,d}, {d,e}, {e,f}, {g,h} are separation pairs.

22. Tri-connected Components A bi-connected graph can be decomposed into its tri-connected components in linear-time using a data structure named SPQR-tree

23. SPQR-Tree virtual edge skeleton

25. Divide-and-Conquer Method Three basic steps: Divide a graph into its tri-connected components. Solve each tri-connected components in a bottom-up fashion. Merge the solutions into a complete one in a top-down fashion. We calculate two possible solutions for each components, namely { s , t } in same color and { s , t } in opposite colors.

26. Example

27. More Technical Details In Hadlock’s algorithm, voronoi graph instead of complete graph is used. A brute-force method is used for solving the maximum weighted planar subgraph problem (could be improved)

28. Conclusions Experiment results show that our method can achieve 3-10X speedup We believe that it is a key to the success of 22nm process Unfortunately we didn’t have chance to try a realistic 32/22nm layout yet because nearly everything is confidential under 90nm Foundries may move to EUV if DPL fails.