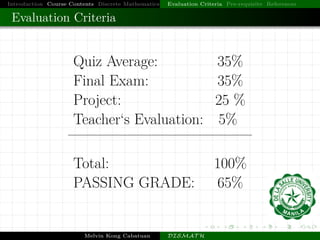
This document introduces a course on discrete mathematics. It provides an overview of the course contents, which are divided into four parts that cover topics like logic, sets, functions, graphs, counting techniques, and computational modeling. The instructor introduces himself and outlines the evaluation criteria, prerequisites, and references for the course. Examples are also provided to illustrate logic puzzles, mathematical reasoning, graph theory, and modeling computation.

1. Introduction Course Contents Discrete Mathematics
DISMAT H
Discrete Mathematics and Its Applications
Welcome to DISMATH!
Melvin Kong Cabatuan
De La Salle University
Manila, Philippines
September 2014
Melvin Kong Cabatuan DISMAT H

2. Introduction Course Contents Discrete Mathematics
Self Introduction
Melvin K. Cabatuan, ECE
Masters of Engineering, NAIST (Japan)
Thesis: Cognitive Radio (Wireless Communication)
IEEE Philippine Section Secretary (2012)
ECE Reviewer/Mentor (Since 2005)
2nd Place, Nov. 2004 ECE Board Exam
Test Engineering Cadet, ON Semiconductors
DOST Academic Excellence Awardee 2004
Mathematician of the Year 2003
DOST Scholar (1999-2004)
Panasonic Scholar, Japan (2007-2010)
Melvin Kong Cabatuan DISMAT H

3. Introduction Course Contents Discrete Mathematics
Melvin Kong Cabatuan DISMAT H

4. Introduction Course Contents Discrete Mathematics
Melvin Kong Cabatuan DISMAT H

5. Introduction Course Contents Discrete Mathematics
Melvin Kong Cabatuan DISMAT H

6. Introduction Course Contents Discrete Mathematics
1 Introduction
2 Course Contents
Evaluation Criteria
Pre-requisite
References
3 Discrete Mathematics
Example
Melvin Kong Cabatuan DISMAT H

7. Introduction Course Contents Discrete Mathematics Evaluation Criteria Pre-requisite References
Course Contents - Part I
1 Logic, Sets, and Functions
2 Methods of Proof, Algorithms, Integers
3 Mathematical Reasoning, Induction, and
Recursion
Melvin Kong Cabatuan DISMAT H

8. Introduction Course Contents Discrete Mathematics Evaluation Criteria Pre-requisite References
Course Contents - Part I
1 Logic, Sets, and Functions
2 Methods of Proof, Algorithms, Integers
3 Mathematical Reasoning, Induction, and
Recursion
Melvin Kong Cabatuan DISMAT H

9. Introduction Course Contents Discrete Mathematics Evaluation Criteria Pre-requisite References
Course Contents - Part I
1 Logic, Sets, and Functions
2 Methods of Proof, Algorithms, Integers
3 Mathematical Reasoning, Induction, and
Recursion
Melvin Kong Cabatuan DISMAT H

10. Introduction Course Contents Discrete Mathematics Evaluation Criteria Pre-requisite References
Course Contents - Part II
1 Relations
2 Graph Theory
3 Planar Graphs, Graph Coloration, and Trees
Melvin Kong Cabatuan DISMAT H

11. Introduction Course Contents Discrete Mathematics Evaluation Criteria Pre-requisite References
Course Contents - Part II
1 Relations
2 Graph Theory
3 Planar Graphs, Graph Coloration, and Trees
Melvin Kong Cabatuan DISMAT H

12. Introduction Course Contents Discrete Mathematics Evaluation Criteria Pre-requisite References
Course Contents - Part II
1 Relations
2 Graph Theory
3 Planar Graphs, Graph Coloration, and Trees
Melvin Kong Cabatuan DISMAT H

13. Introduction Course Contents Discrete Mathematics Evaluation Criteria Pre-requisite References
Course Contents - Part III
1 Counting Techniques and Probability Theory
2 Advance Counting Techniques
Melvin Kong Cabatuan DISMAT H

14. Introduction Course Contents Discrete Mathematics Evaluation Criteria Pre-requisite References
Course Contents - Part III
1 Counting Techniques and Probability Theory
2 Advance Counting Techniques
Melvin Kong Cabatuan DISMAT H

15. Introduction Course Contents Discrete Mathematics Evaluation Criteria Pre-requisite References
Course Contents - Part III
1 Counting Techniques and Probability Theory
2 Advance Counting Techniques
Melvin Kong Cabatuan DISMAT H

16. Introduction Course Contents Discrete Mathematics Evaluation Criteria Pre-requisite References
Course Contents - Part IV
1 Modeling Computation, Finite State
Machines and Automata
2 Algebraic Systems and Formal Languages
Melvin Kong Cabatuan DISMAT H

17. Introduction Course Contents Discrete Mathematics Evaluation Criteria Pre-requisite References
Course Contents - Part IV
1 Modeling Computation, Finite State
Machines and Automata
2 Algebraic Systems and Formal Languages
Melvin Kong Cabatuan DISMAT H

18. Introduction Course Contents Discrete Mathematics Evaluation Criteria Pre-requisite References
Evaluation Criteria
Quiz Average: 35%
Final Exam: 35%
Project: 25 %
Teacher‘s Evaluation: 5%
Total: 100%
PASSING GRADE: 65%
Melvin Kong Cabatuan DISMAT H

19. Introduction Course Contents Discrete Mathematics Evaluation Criteria Pre-requisite References
Pre-requisite
1 ENGALG1 (Hard)
2 Mathematical Background (High-school
mathematics should be enough if ...)
3 A curious mind!
Melvin Kong Cabatuan DISMAT H

20. Introduction Course Contents Discrete Mathematics Evaluation Criteria Pre-requisite References
Pre-requisite
1 ENGALG1 (Hard)
2 Mathematical Background (High-school
mathematics should be enough if ...)
3 A curious mind!
Melvin Kong Cabatuan DISMAT H

21. Introduction Course Contents Discrete Mathematics Evaluation Criteria Pre-requisite References
Pre-requisite
1 ENGALG1 (Hard)
2 Mathematical Background (High-school
mathematics should be enough if ...)
3 A curious mind!
Melvin Kong Cabatuan DISMAT H

22. Introduction Course Contents Discrete Mathematics Evaluation Criteria Pre-requisite References
References
1 Rosen, K.H. (2012). Discrete Mathematics
and Its Applications (7 ed.), New York,
McGraw-Hill
2 Online Resources
Melvin Kong Cabatuan DISMAT H

23. Introduction Course Contents Discrete Mathematics Evaluation Criteria Pre-requisite References
References
1 Rosen, K.H. (2012). Discrete Mathematics
and Its Applications (7 ed.), New York,
McGraw-Hill
2 Online Resources
Melvin Kong Cabatuan DISMAT H

24. Introduction Course Contents Discrete Mathematics Example
Discrete Mathematics
Definition
c Study of distinct & countable objects. d
Melvin Kong Cabatuan DISMAT H

25. Introduction Course Contents Discrete Mathematics Example
Discrete Mathematics
Purpose
To provides the mathematical foundation
for many computer engineering/science
courses including data structures,
algorithms, database theory, automata
theory, formal languages, etc . . .
Melvin Kong Cabatuan DISMAT H

26. Introduction Course Contents Discrete Mathematics Example
Discrete Mathematics
Insight
c It excludes ’continuous mathematics’
such as Calculus. d
Melvin Kong Cabatuan DISMAT H

27. Introduction Course Contents Discrete Mathematics Example
Logic Example: Knights and Knaves
An island is inhabited only by knights and
knaves. Knights always tell the truth, and
knaves always lie.You meet two inhabitants:
Mel and Vin. Determine what Mel and Vin
is, if they say:
Mel: c Vin is a knight d
Vin: c The two of us are opposite types d
Melvin Kong Cabatuan DISMAT H

28. Introduction Course Contents Discrete Mathematics Example
Logic Example: Knights and Knaves
An island is inhabited only by knights and
knaves. Knights always tell the truth, and
knaves always lie.You meet two inhabitants:
Mel and Vin. Determine what Mel and Vin
is, if they say:
Mel: c Vin is a knight d
Vin: c The two of us are opposite types d
∴ Both Mel and Vin are Knaves!
Melvin Kong Cabatuan DISMAT H

29. Introduction Course Contents Discrete Mathematics Example
Logic Example: Knights and Knaves
An island is inhabited only by knights and
knaves. Knights always tell the truth, and
knaves always lie.You meet two inhabitants:
Mel and Vin. Determine what Mel and Vin
is, if they say:
Mel: c We are both knaves d
Vin: c ... d
Melvin Kong Cabatuan DISMAT H

30. Introduction Course Contents Discrete Mathematics Example
Logic Example: Knights and Knaves
An island is inhabited only by knights and
knaves. Knights always tell the truth, and
knaves always lie.You meet two inhabitants:
Mel and Vin. Determine what Mel and Vin
is, if they say:
Mel: c We are both knaves d
Vin: c ... d
∴ Mel is a Knave and Vin is a Knight!
Melvin Kong Cabatuan DISMAT H

31. Introduction Course Contents Discrete Mathematics Example
Example: Mathematical Reasoning/ Counting
A pyramid scheme promises participants
payment, services, primarily for enrolling
other people into the scheme or training
them to take part, rather than supplying
any real investment or sale of products.
Melvin Kong Cabatuan DISMAT H

32. Introduction Course Contents Discrete Mathematics Example
Example: Graph Theory/ Mapping
Facebook Map of the World.
Melvin Kong Cabatuan DISMAT H

33. Introduction Course Contents Discrete Mathematics Example
Example: Trees
Linux Directory.
Melvin Kong Cabatuan DISMAT H

34. Introduction Course Contents Discrete Mathematics Example
Example: Modeling Computation
Kasparov vs. Deep Blue.
Melvin Kong Cabatuan DISMAT H

35. Introduction Course Contents Discrete Mathematics Example
Key Insights
Melvin Kong Cabatuan DISMAT H

36. Introduction Course Contents Discrete Mathematics Example
Key Insights
Discrete Mathematics is the study of distinct
& countable objects.
Melvin Kong Cabatuan DISMAT H

37. Introduction Course Contents Discrete Mathematics Example
Key Insights
Discrete Mathematics is the study of distinct
& countable objects.
It provides the mathematical foundation for many
computer engineering/science courses including
data structures, algorithms, database theory,
automata theory, formal languages, etc . . .
Melvin Kong Cabatuan DISMAT H

38. Introduction Course Contents Discrete Mathematics Example
Key Insights
Discrete Mathematics is the study of distinct
& countable objects.
It provides the mathematical foundation for many
computer engineering/science courses including
data structures, algorithms, database theory,
automata theory, formal languages, etc . . .
c It finds its application in our everyday lives. d
Melvin Kong Cabatuan DISMAT H

39. Introduction Course Contents Discrete Mathematics Example
Shall we begin!
c Thank you for your attention d
Melvin Kong Cabatuan DISMAT H