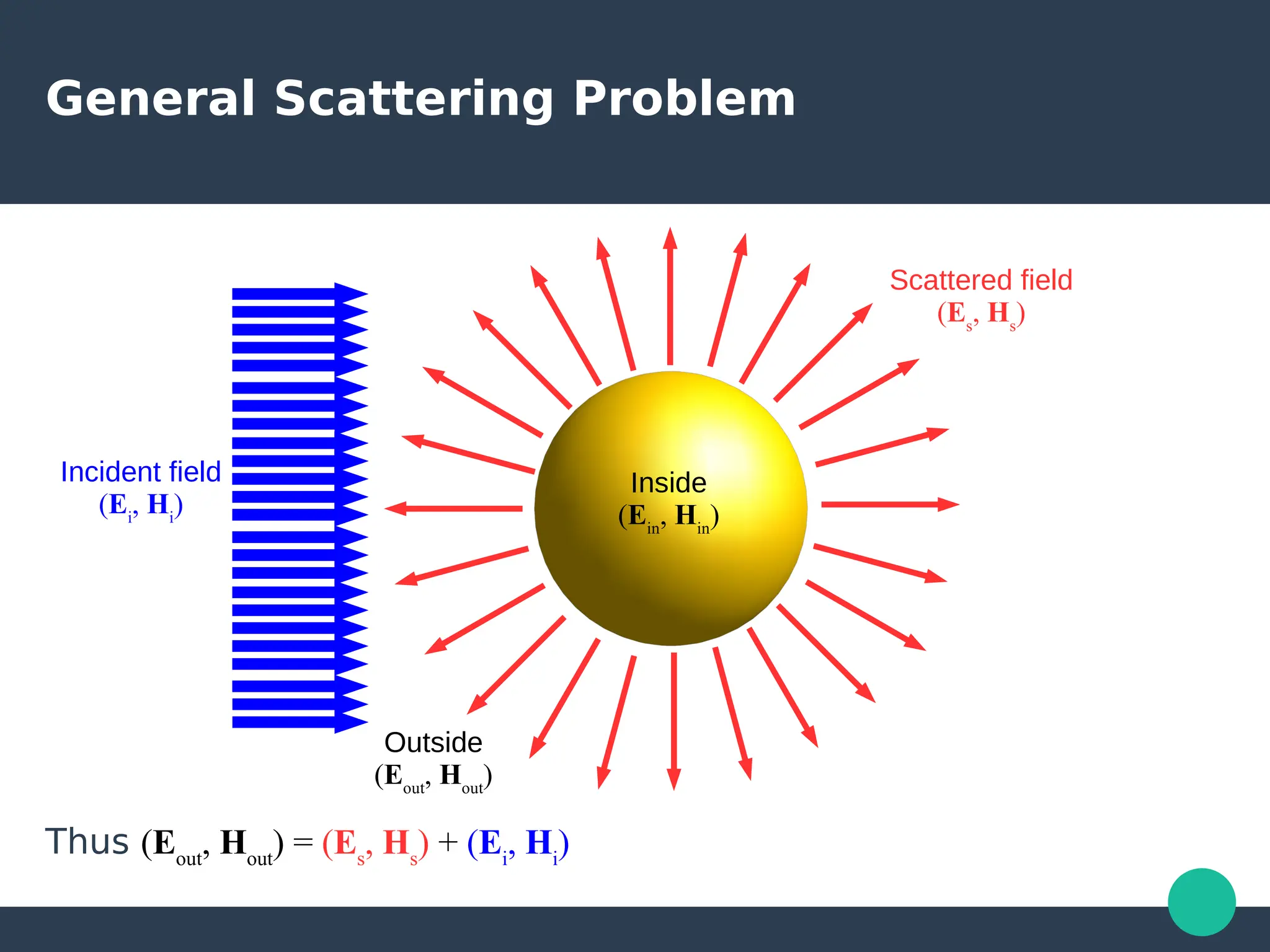
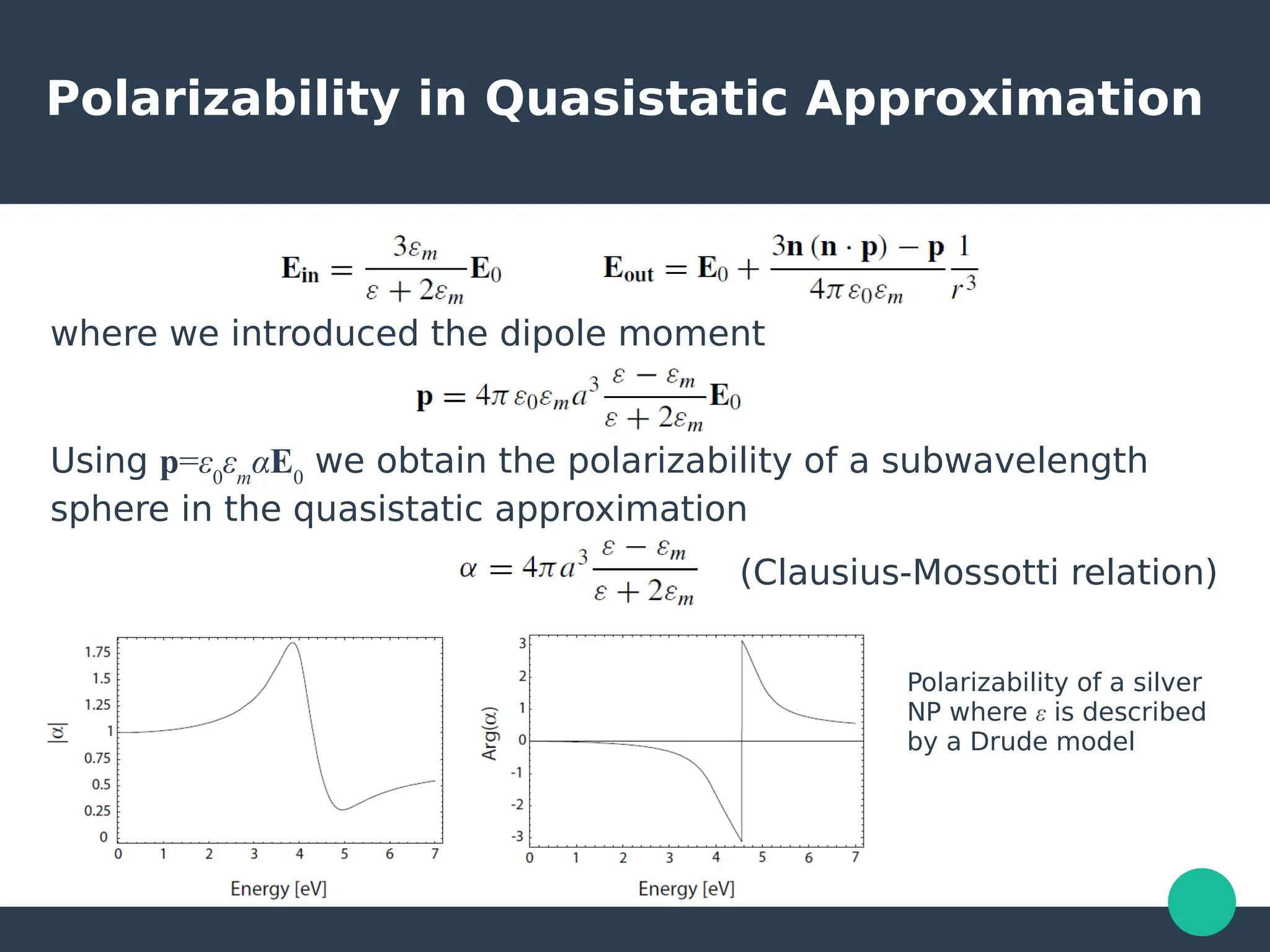
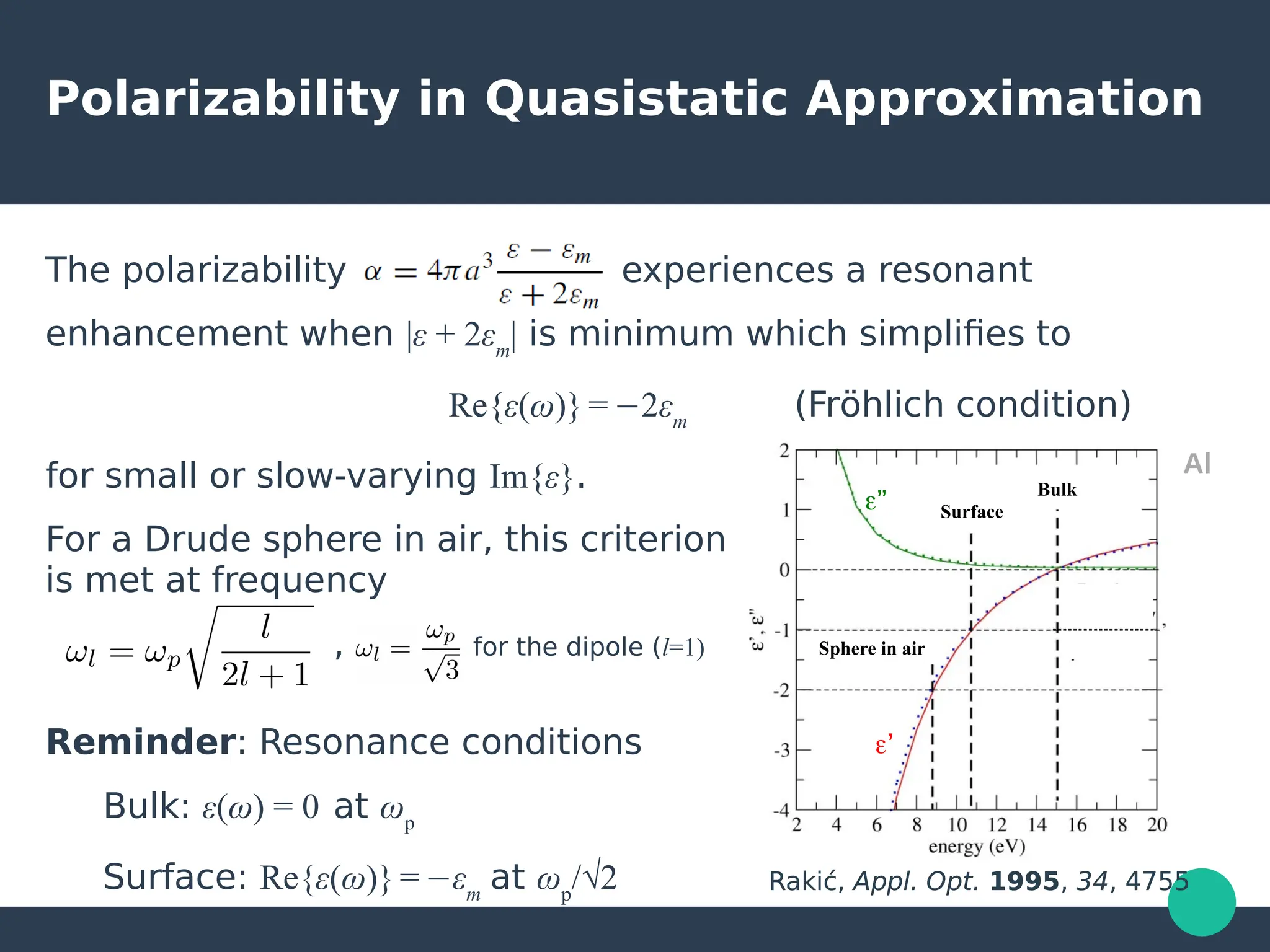
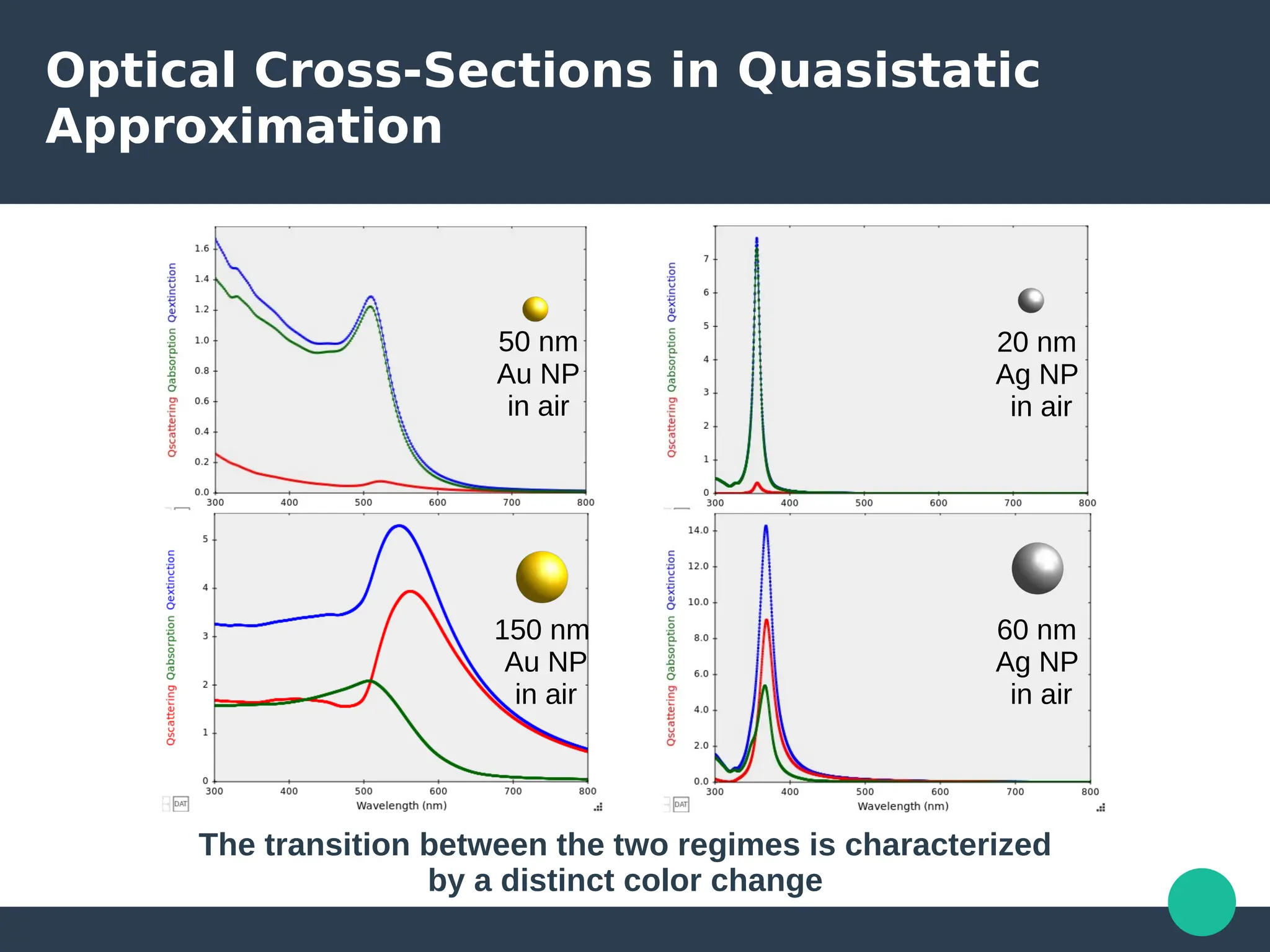
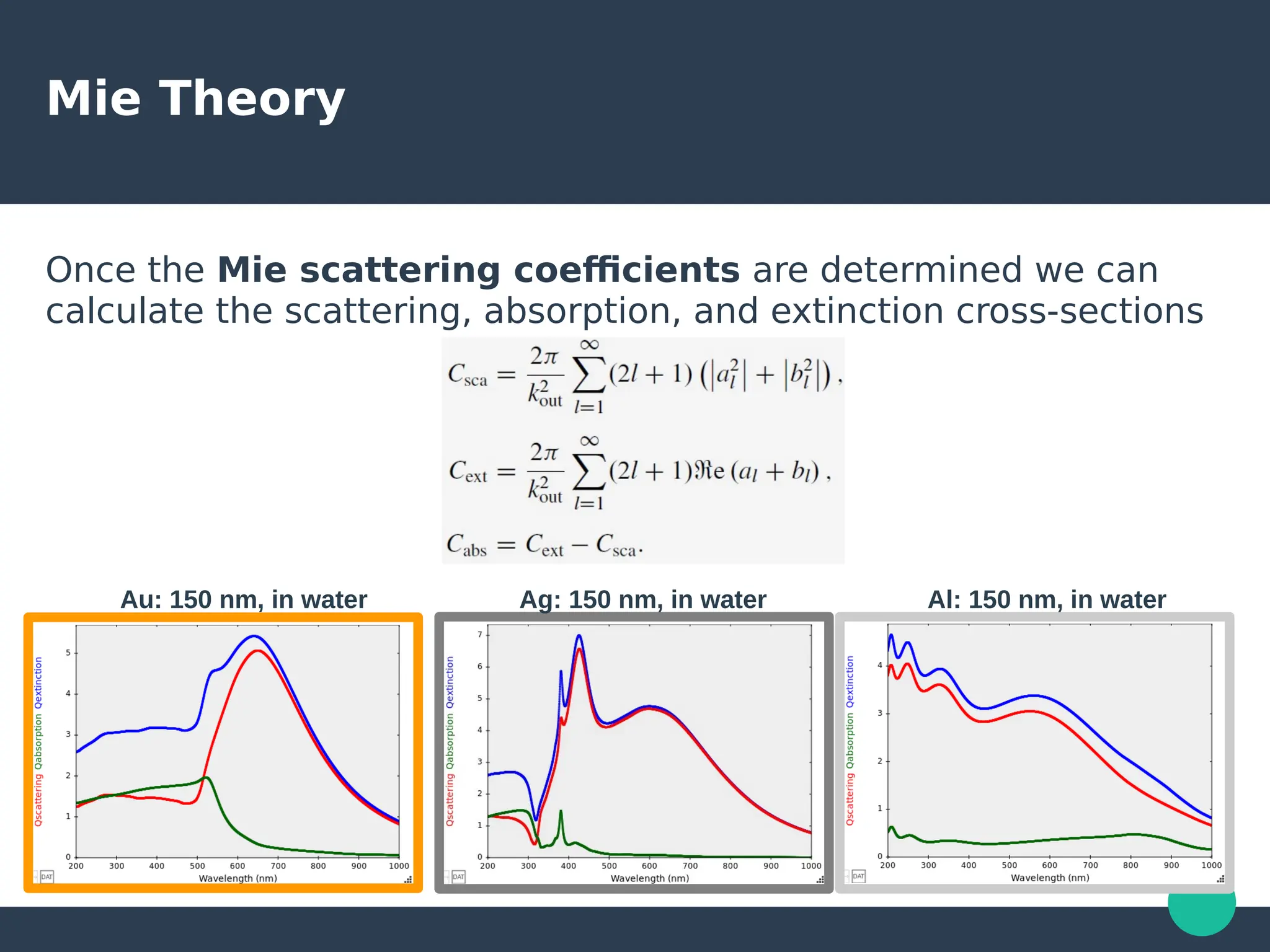
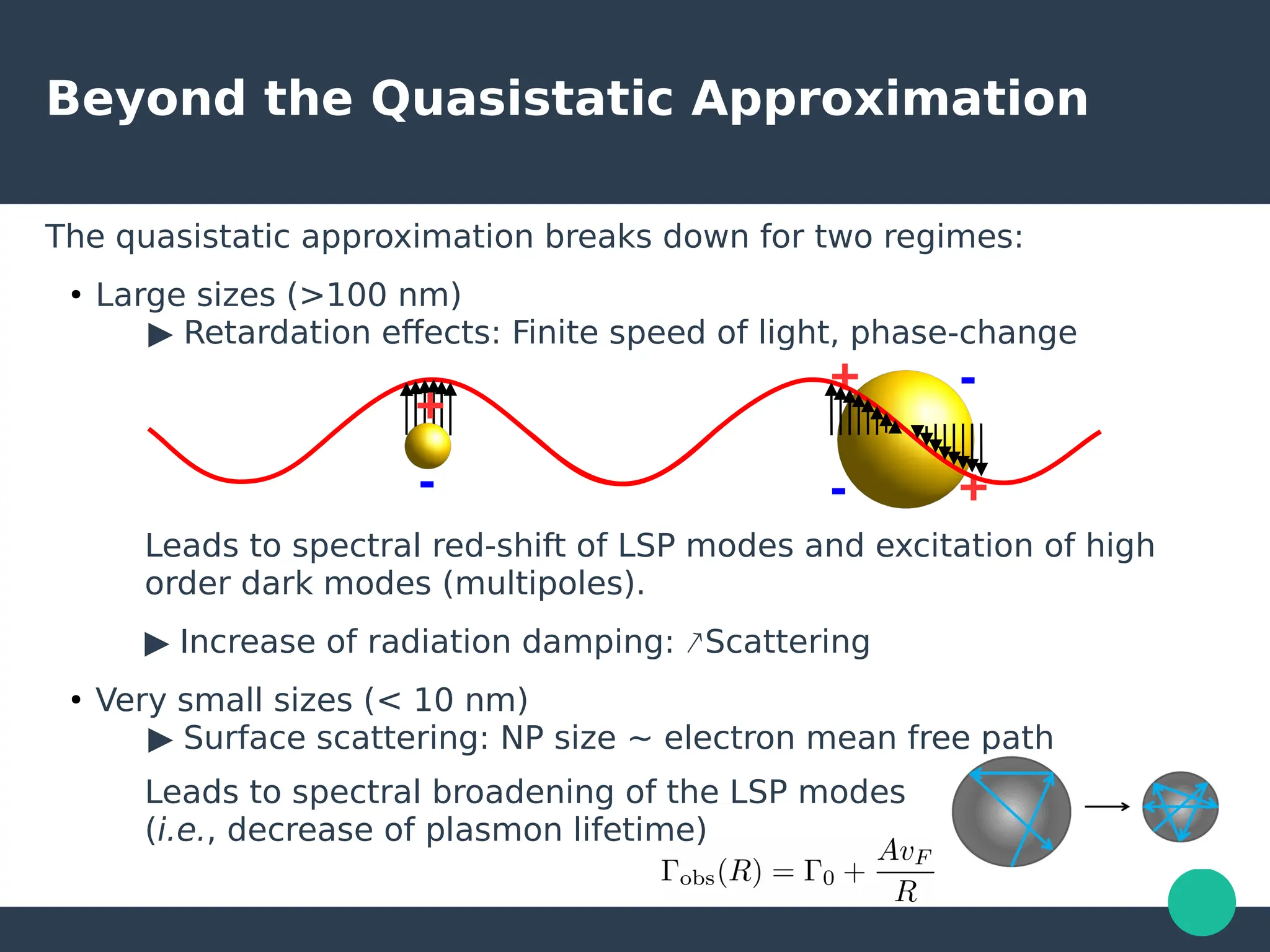
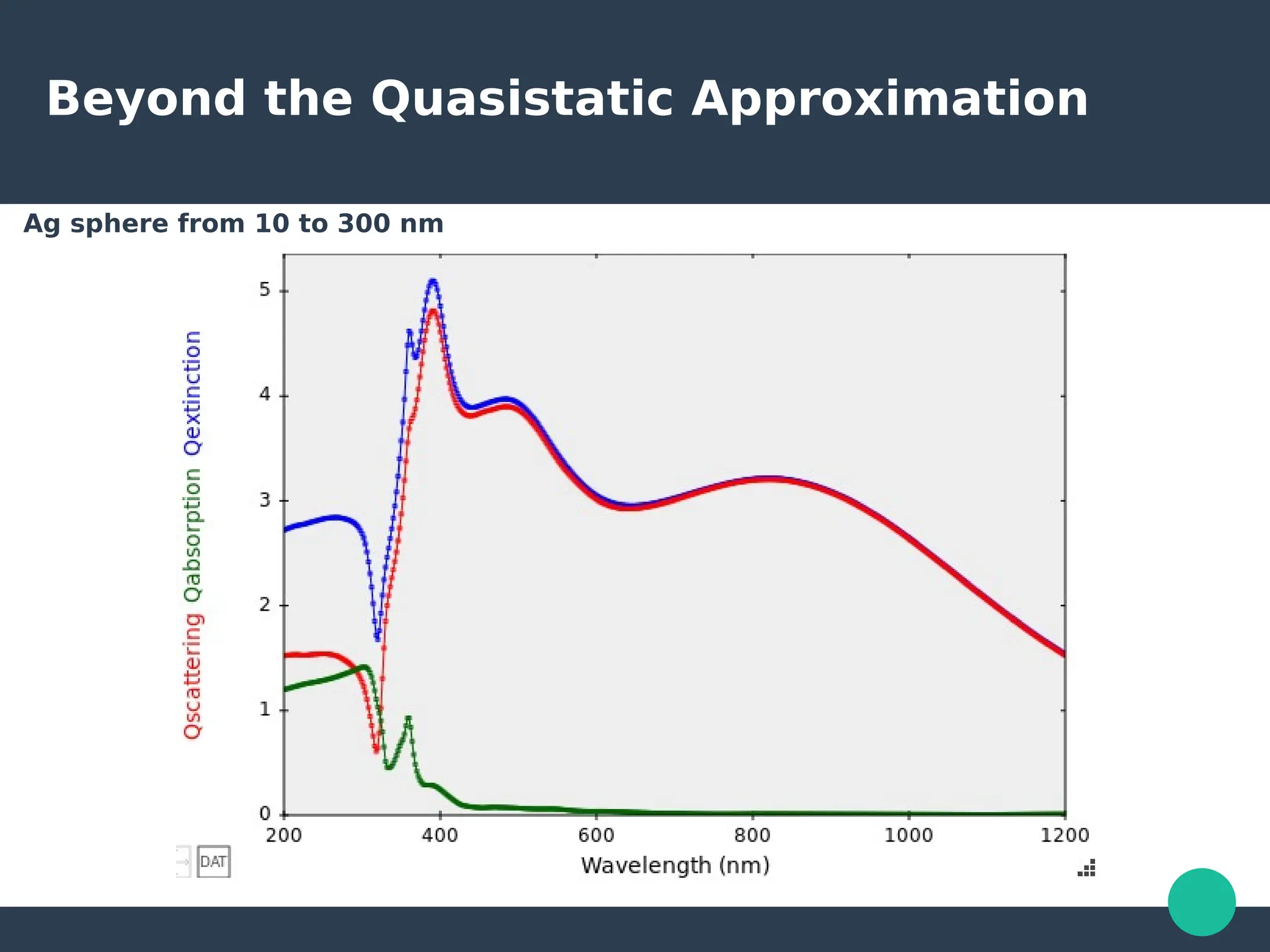
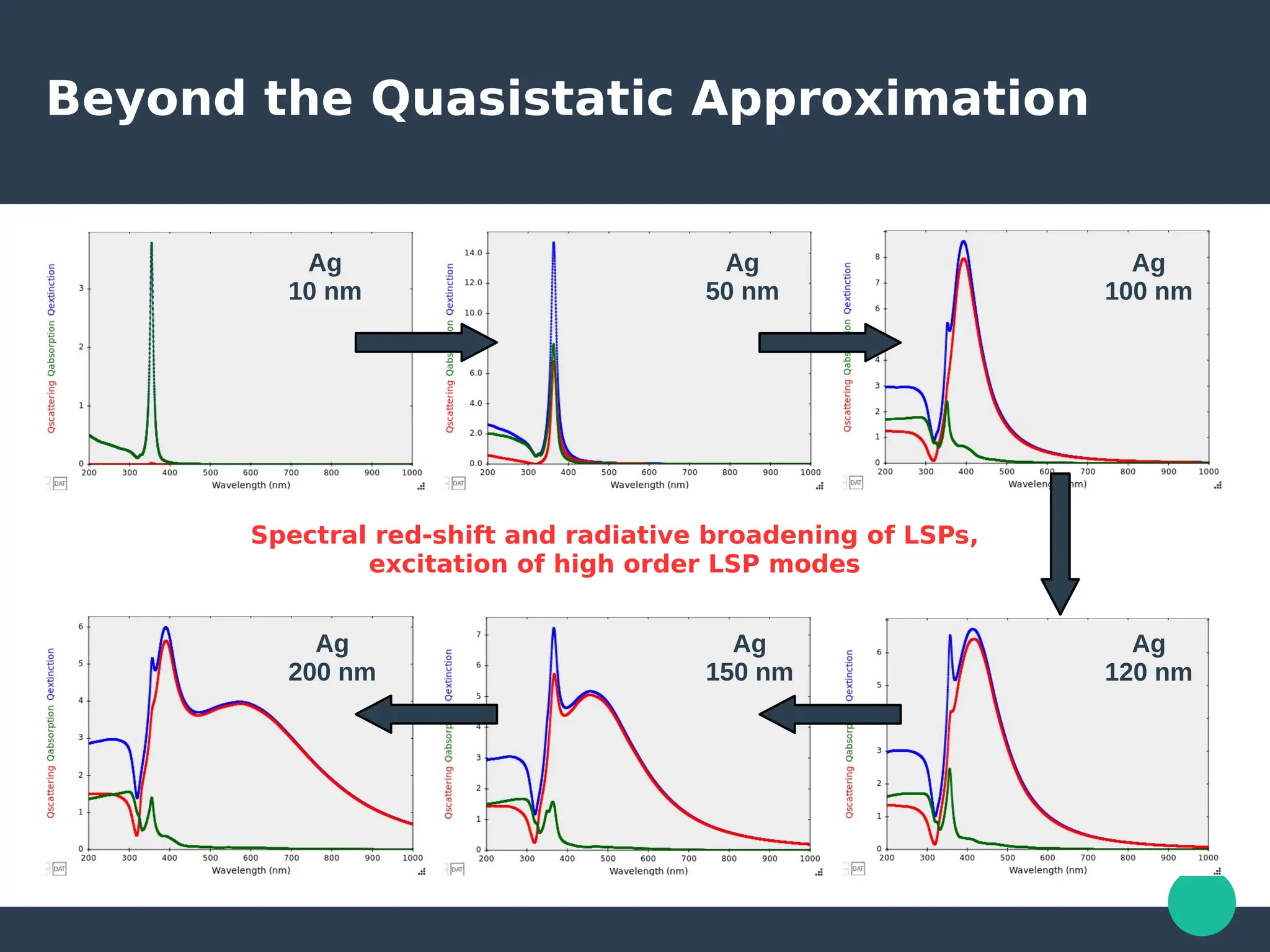
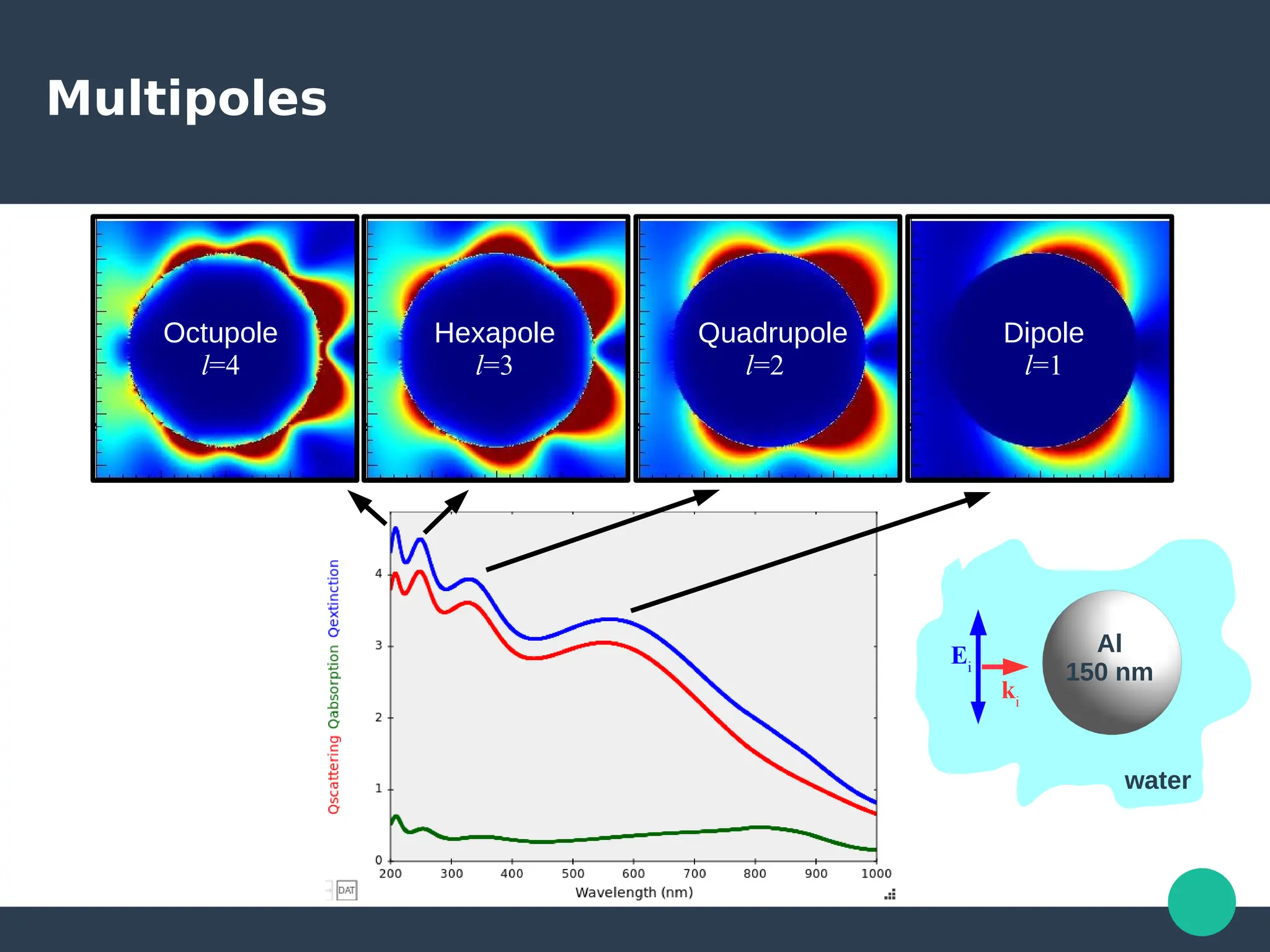
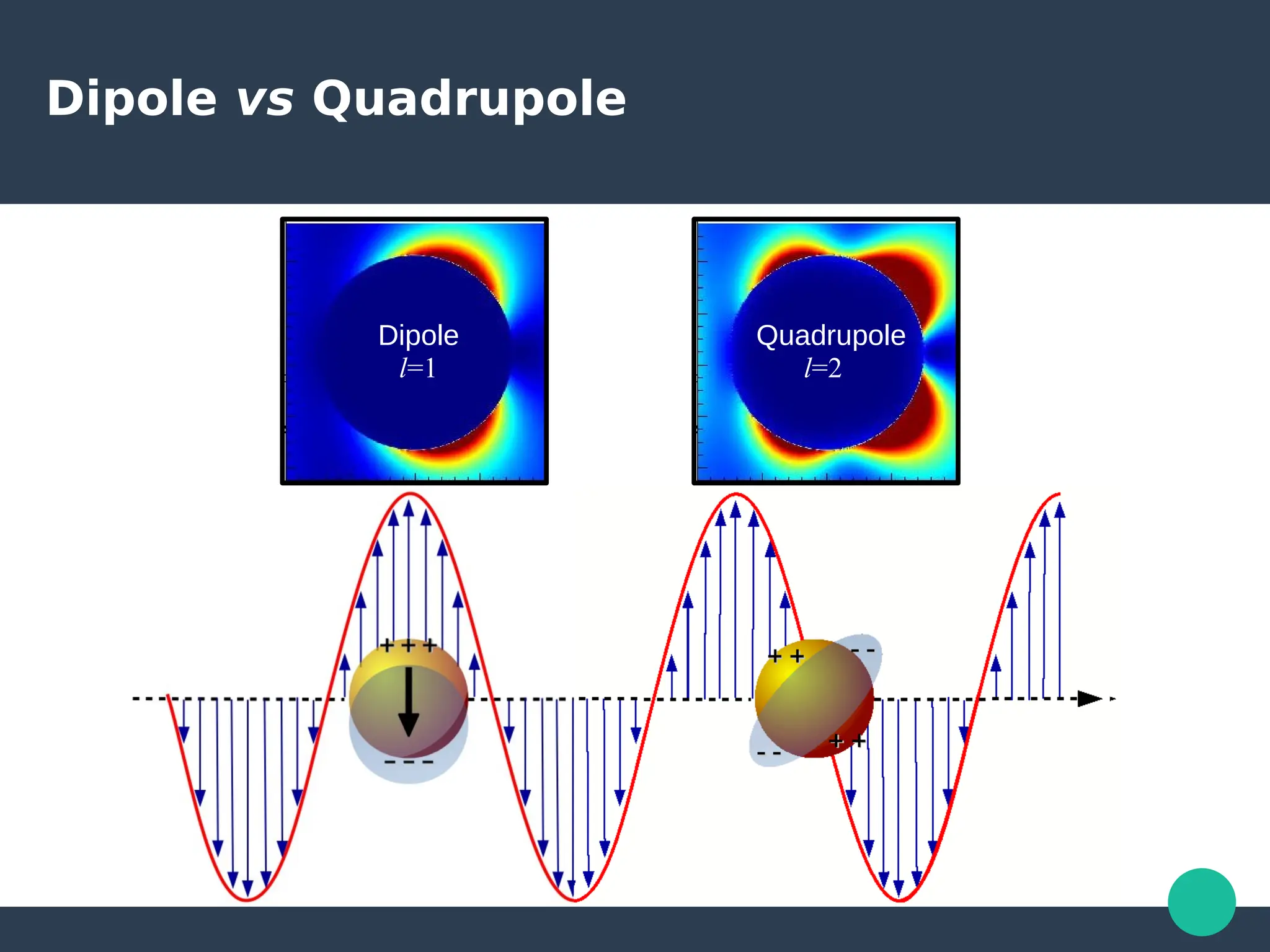
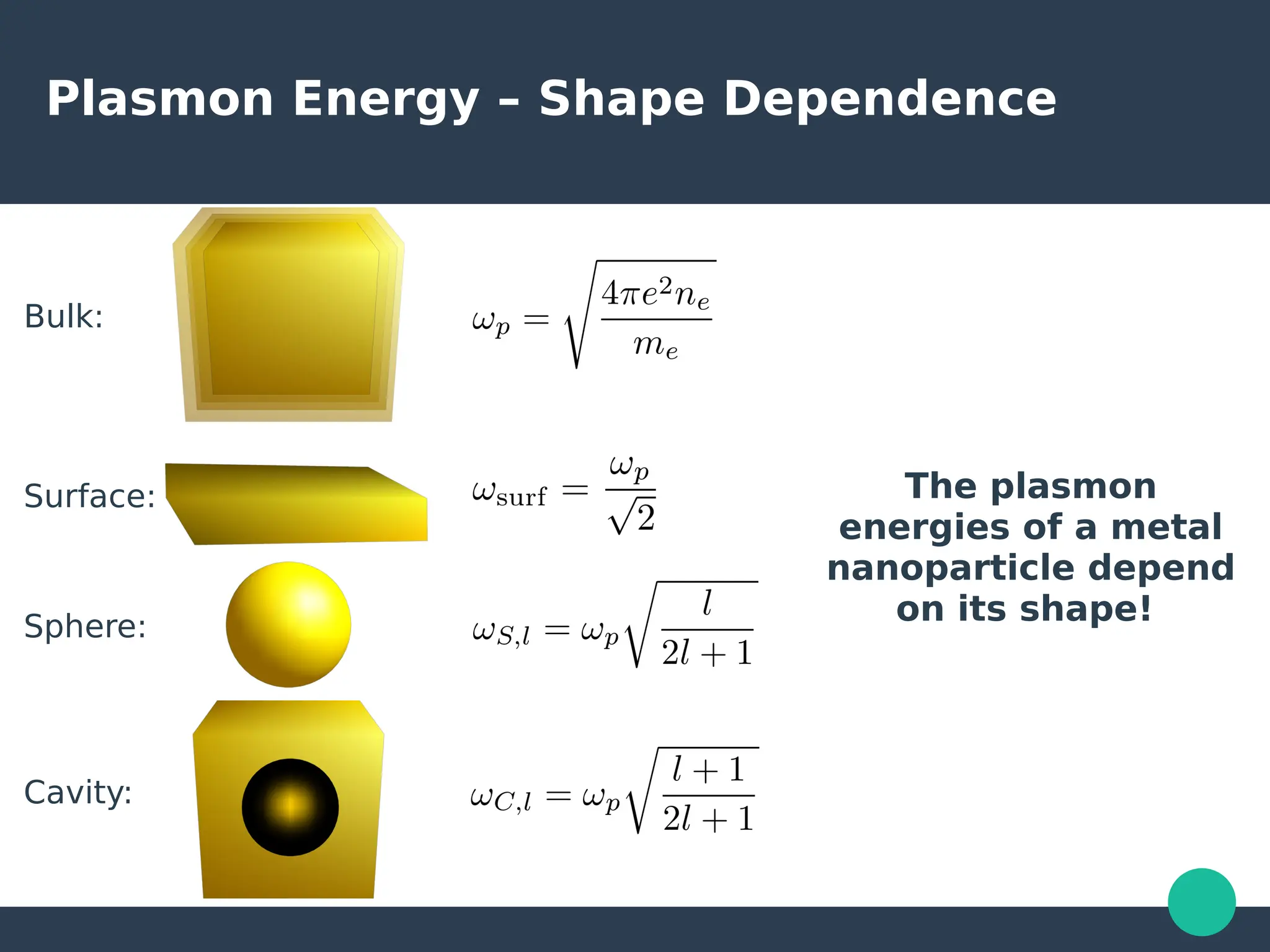
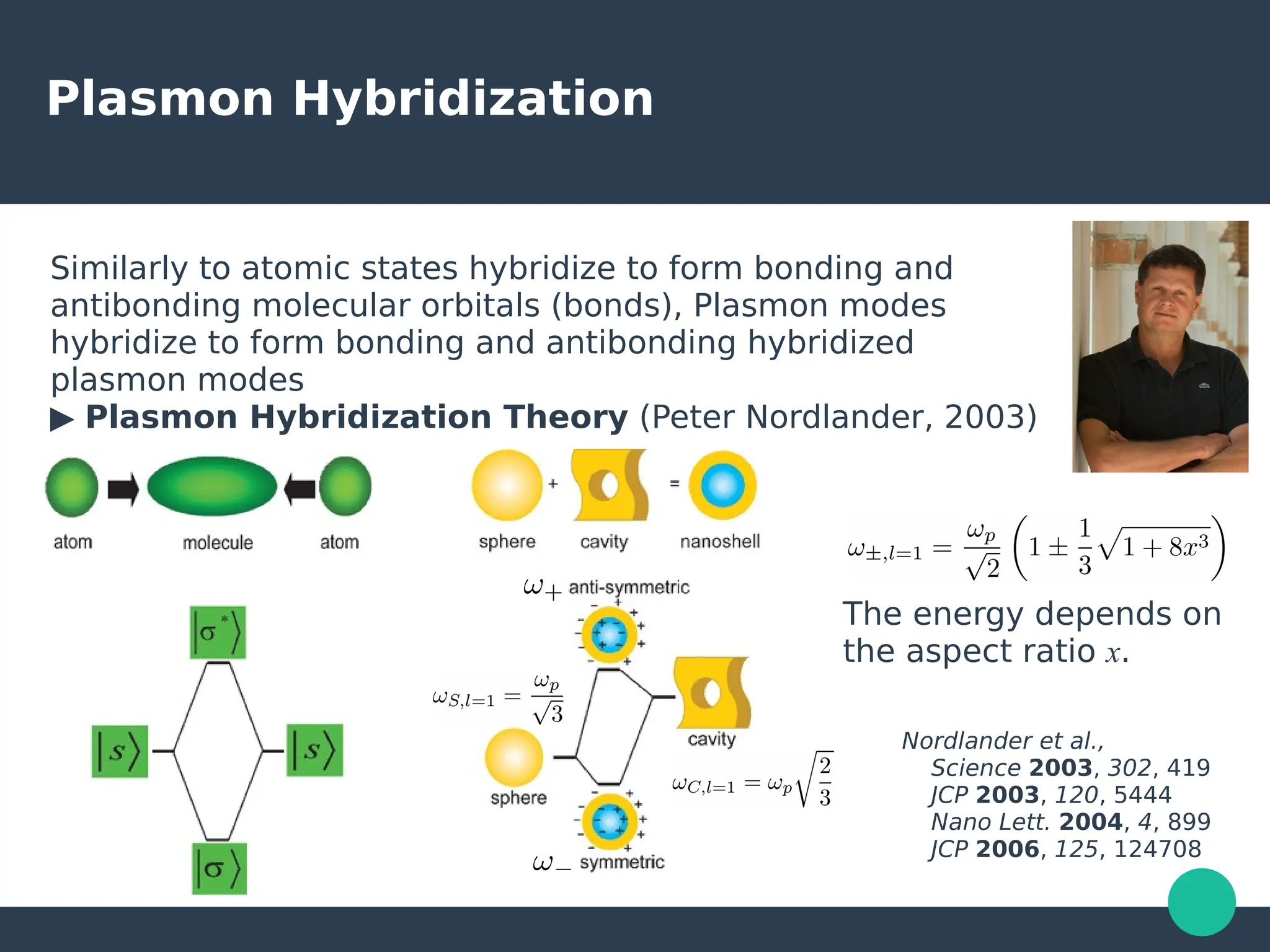
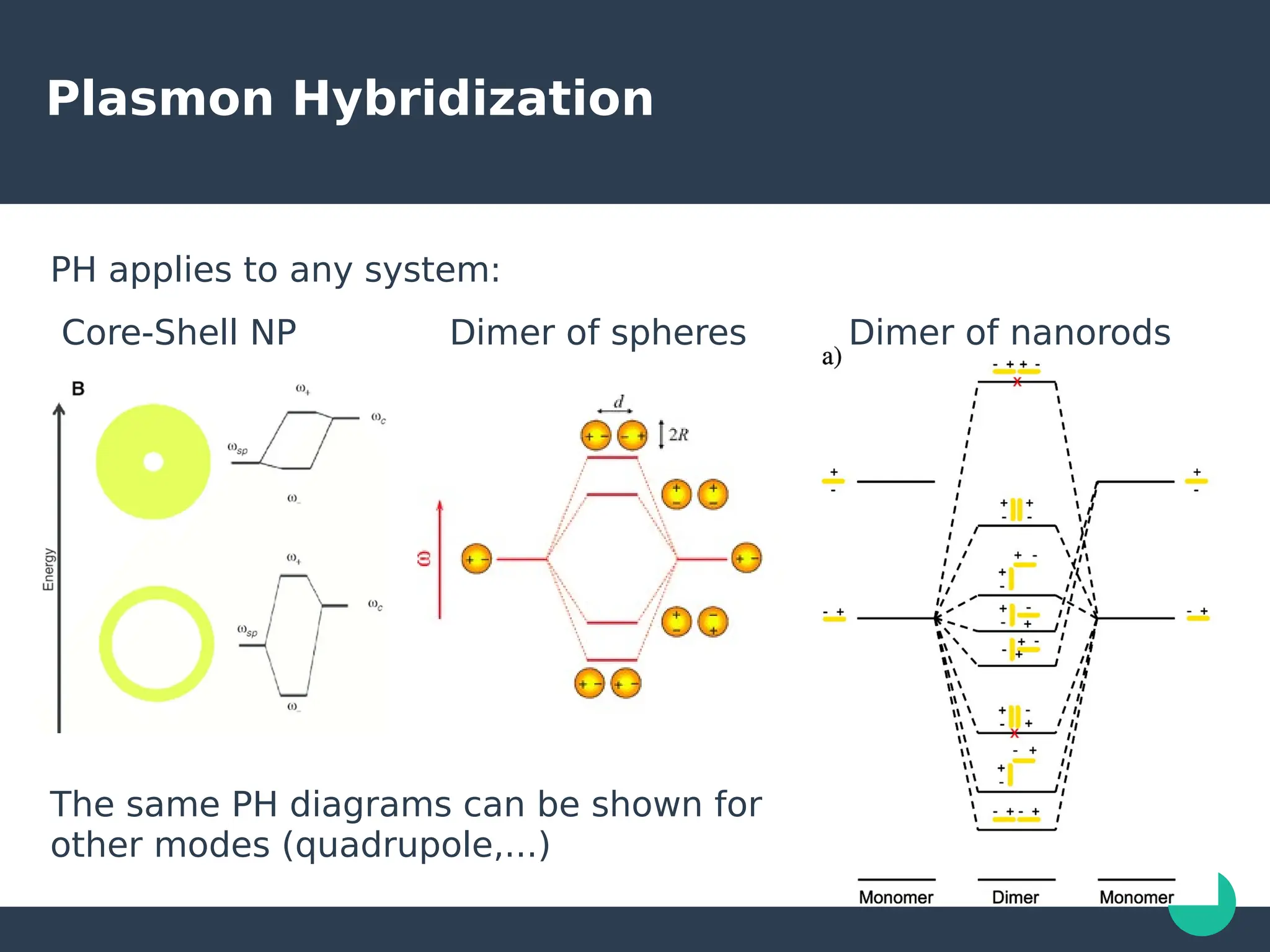
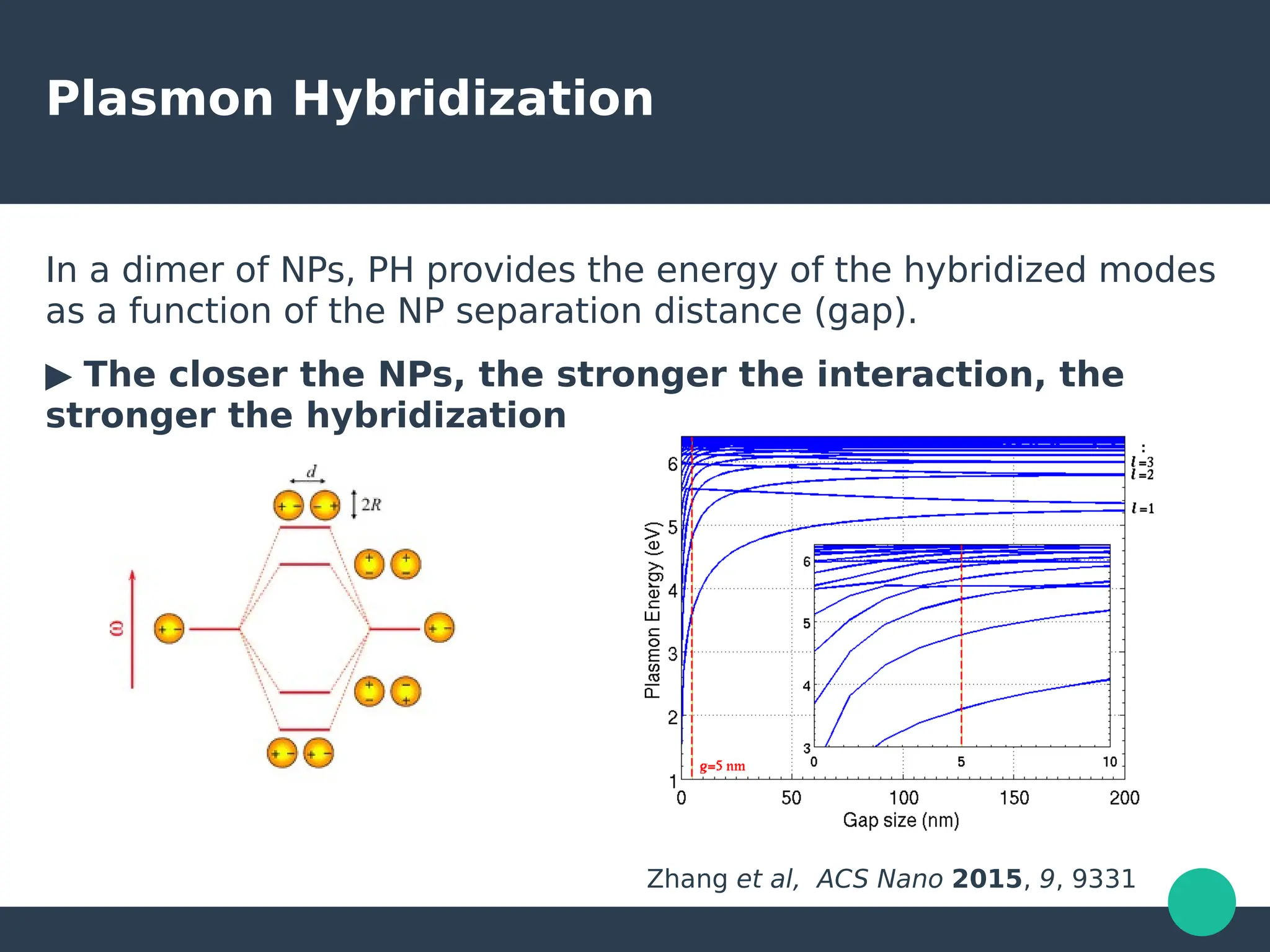
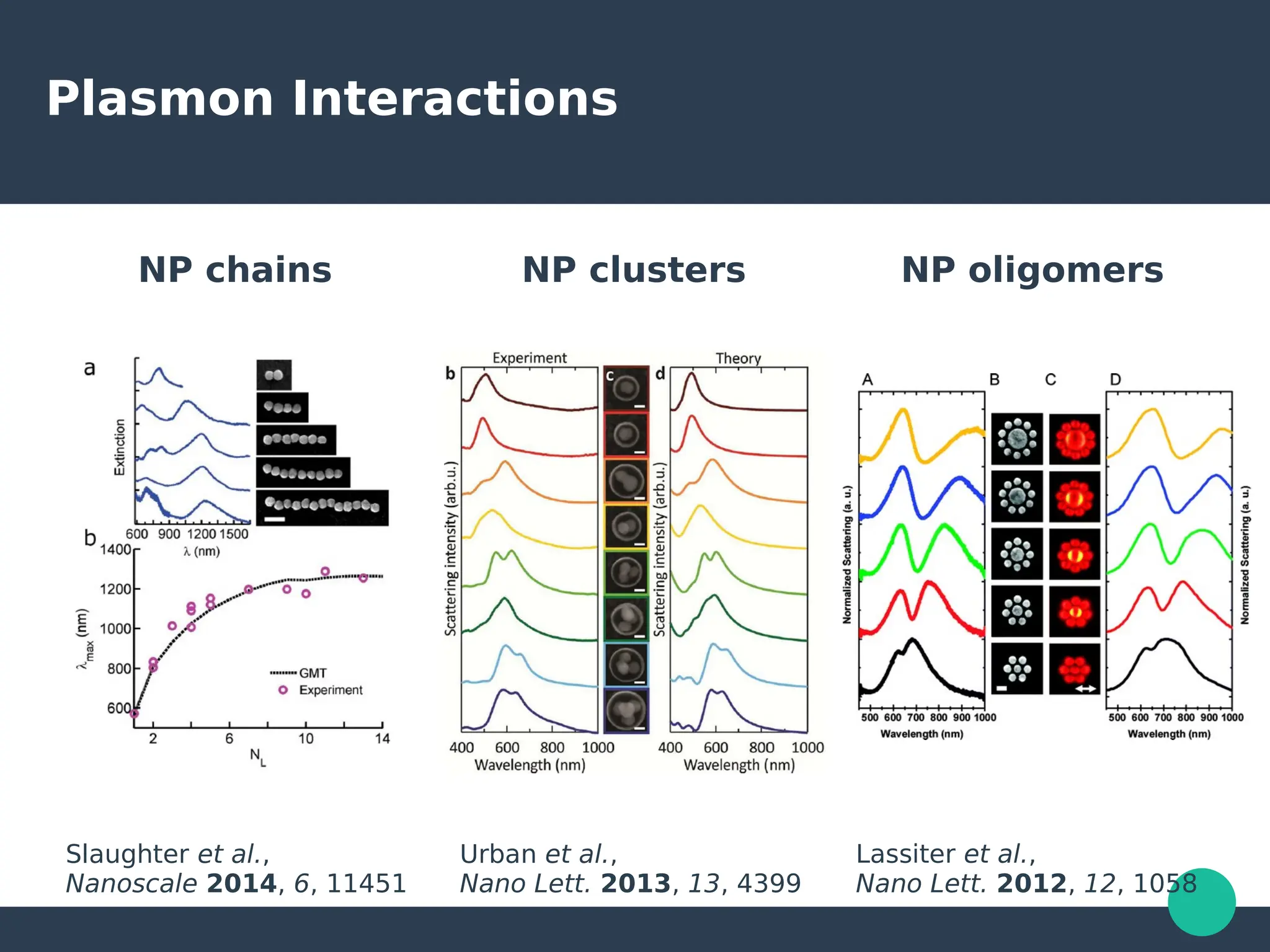
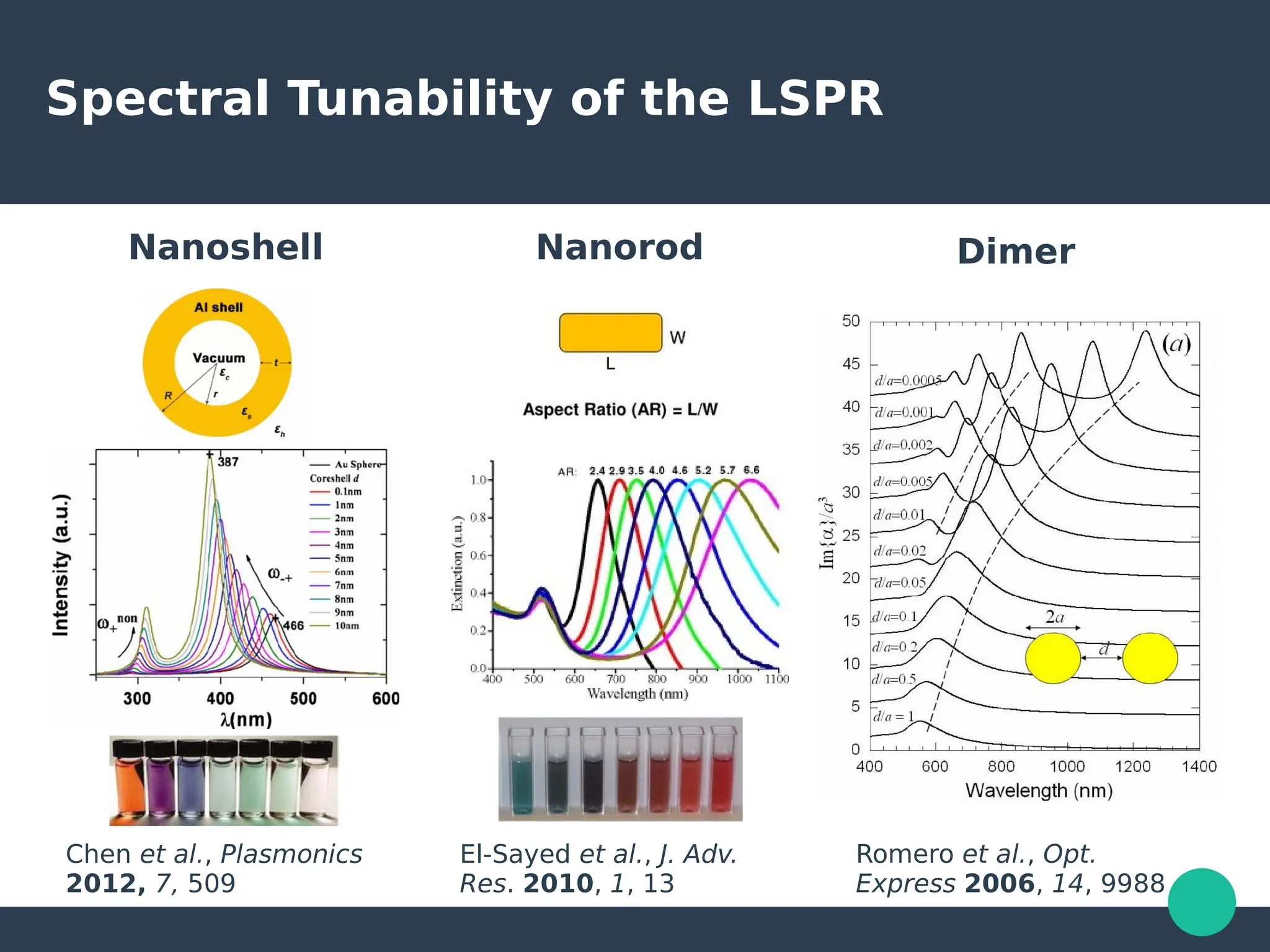
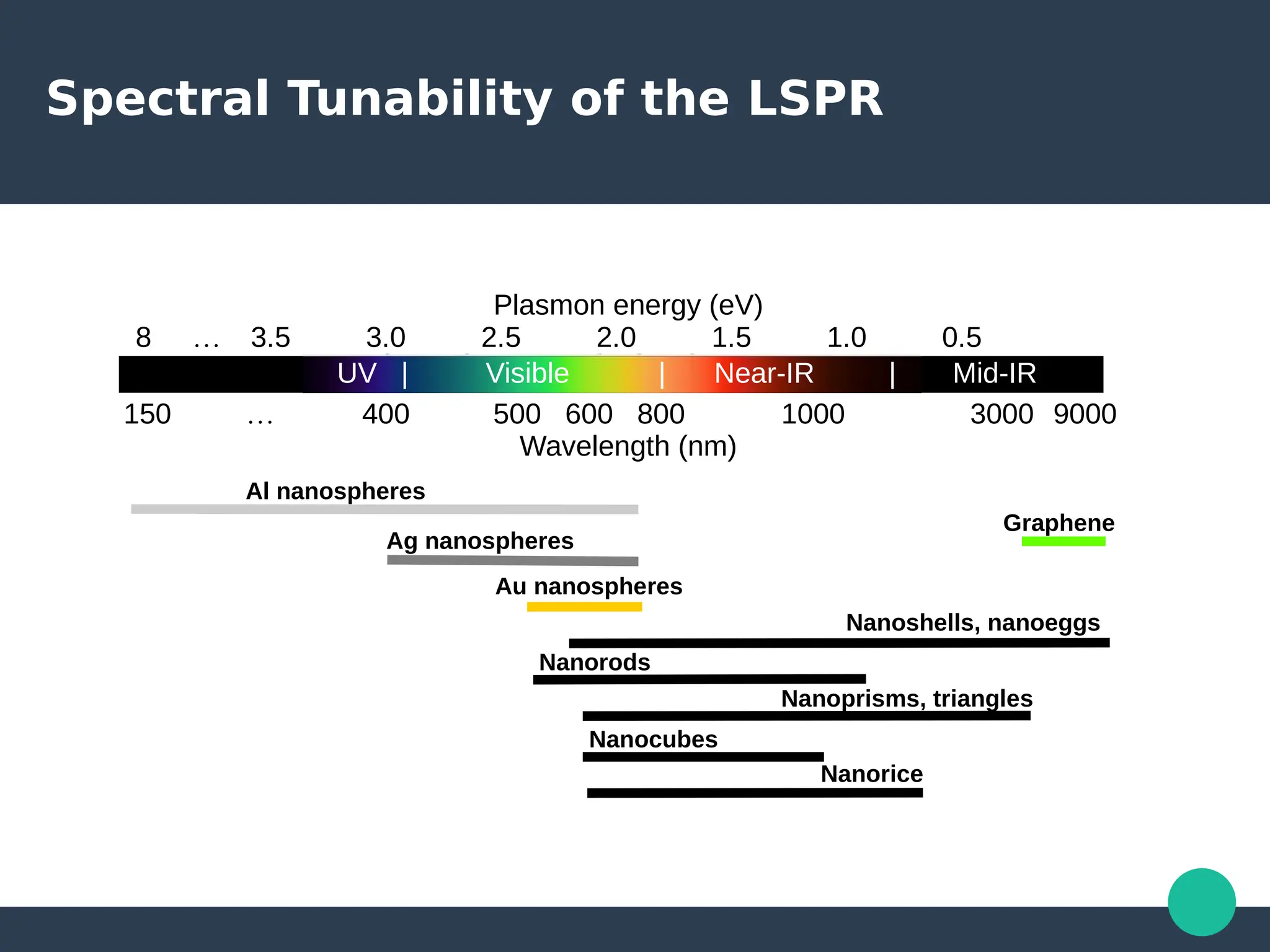
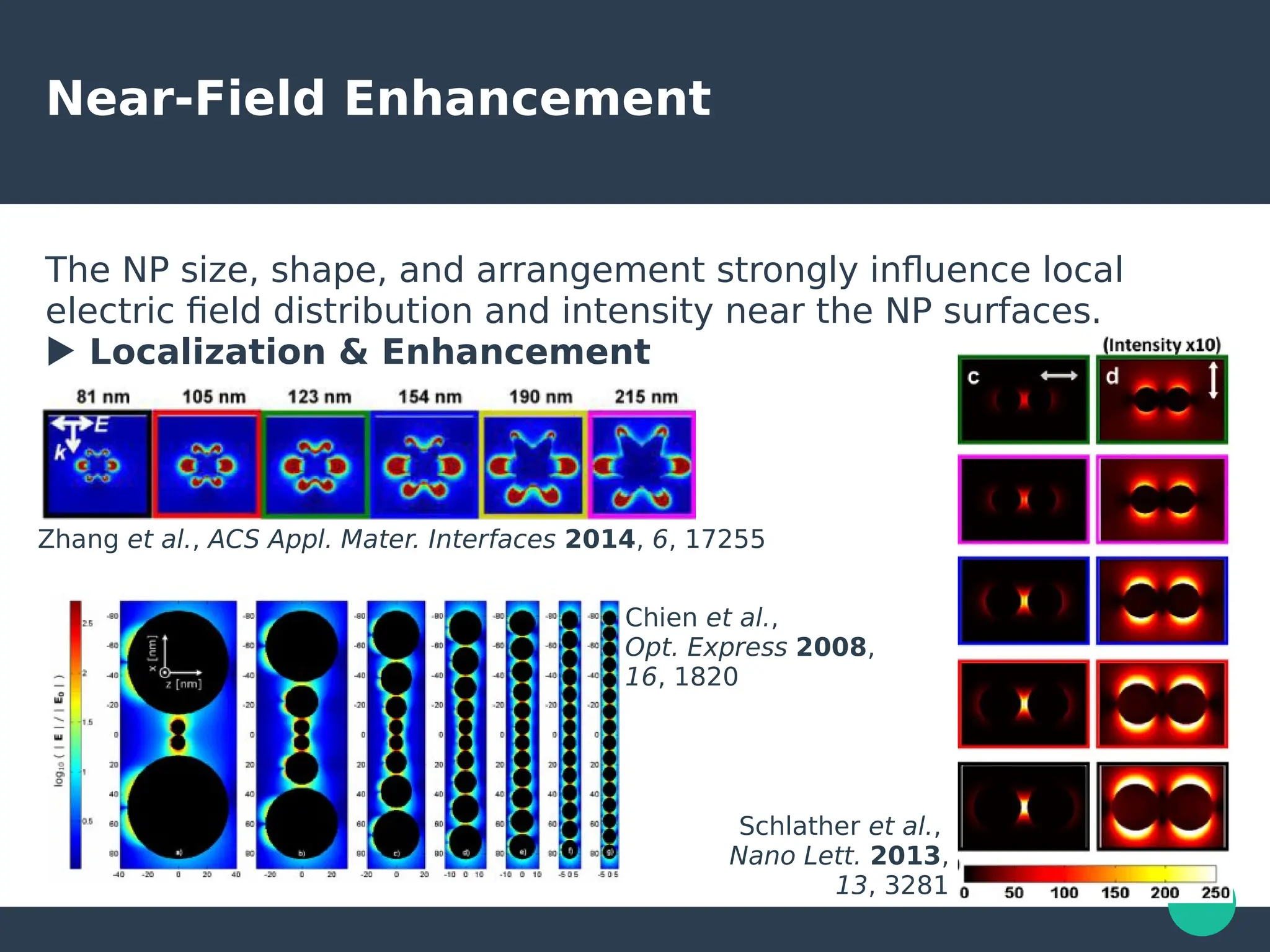
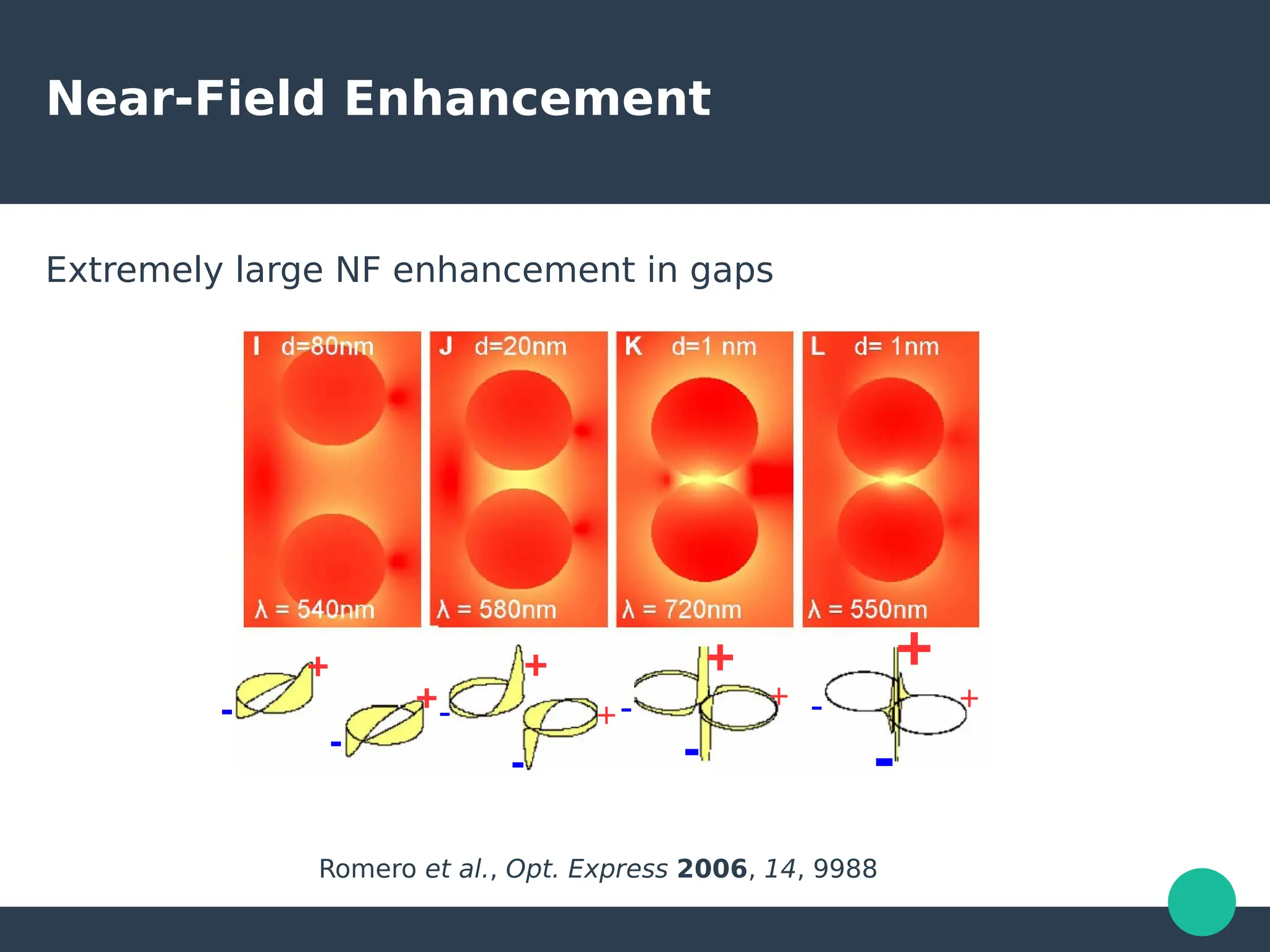
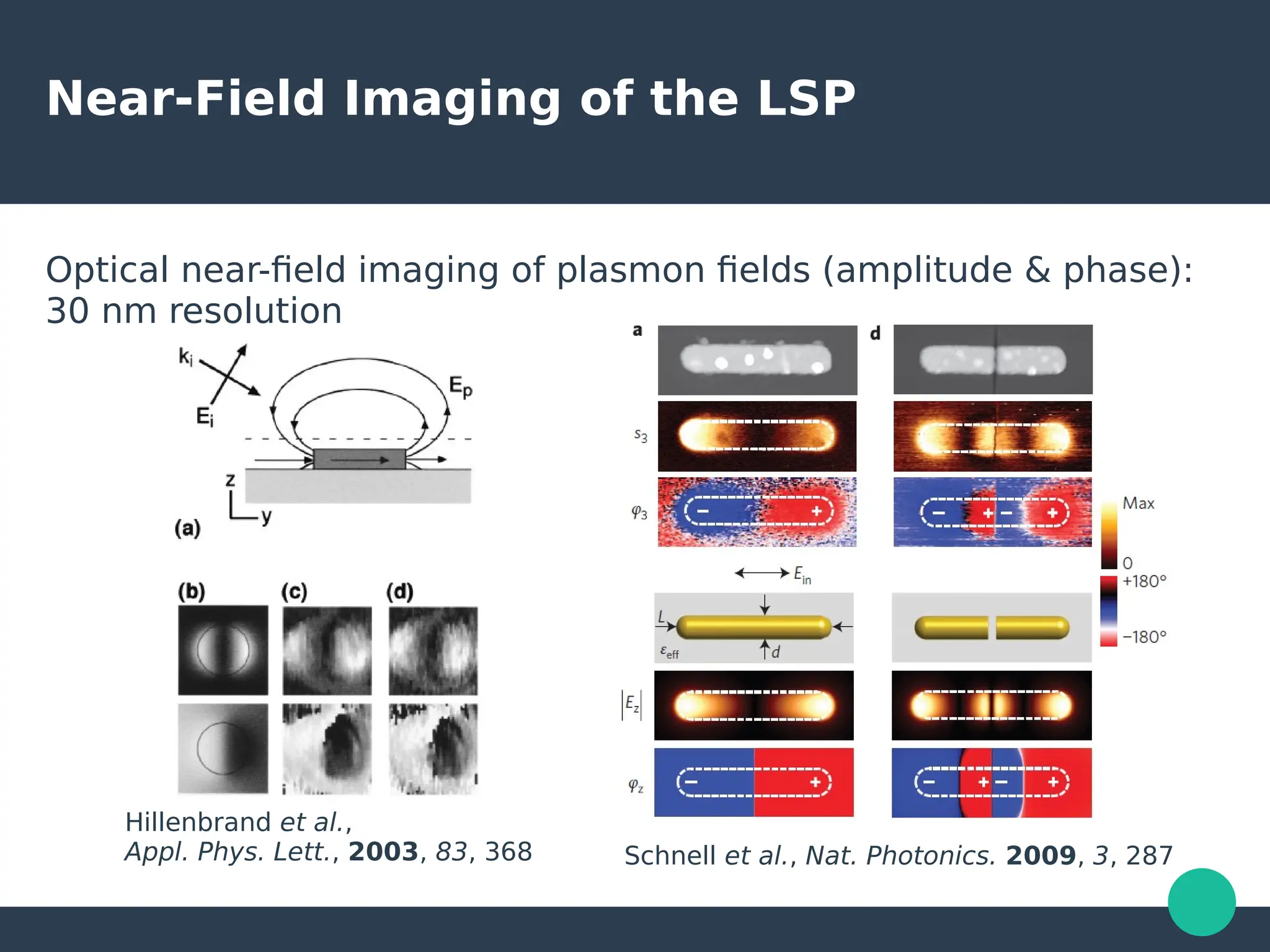
Localized surface plasmons (LSPs) are non-propagating oscillations of free electron gas confined to metallic nanoparticles that are much smaller than the wavelength of light. In the quasistatic approximation, the interaction of light with a nanoparticle can be described by the polarizability and optical cross-sections. For larger nanoparticles, Mie theory provides an analytical solution by describing the scattering fields using vector spherical harmonics. The plasmon resonance depends on the nanoparticle size, shape, composition, and local environment.

1. Chapter 9 |
Localized Surface
Plasmons (LSP)

2. Introduction
We have seen that metals sustain collective, coherent, and
incompressible oscillations of the free conduction electron
gas, known as plasmons.
These modes exist in bulk materials: bulk plasmon
These modes also appear as a results of Maxwell’s equations at
metal-dielectric interfaces: surface plasmon
What about a finite-size metallic objects that also possesses metal-
dielectic interfaces?
▶Yes! We introduce another fundamental excitation of plasmonics:
localized surface plasmon (LSP)

3. Charge Density Oscillation in a NP
Because the NP is much smaller
than the wavelength of incident
field, the NP gets polarized
▶ Restoring force arises
▶ Plasmonic oscillation is
formed
(cf. harmonic oscillator model)
Whereas SPP are propagating
surface modes, LSP are non-
propagating, they are localized.

4. General Scattering Problem
Thus (Eout
, Hout
) = (Es
, Hs
) + (Ei
, Hi
)
Incident field
(Ei
, Hi
)
Scattered field
(Es
, Hs
)
Outside
(Eout
, Hout
)
Inside
(Ein
, Hin
)

5. Quasistatic Approximation
Rayleigh theory
The interaction of light w/ a subwavelength NP of size a can be
described in the quasistatic approximation (Rayleigh theory)
if a≪λ.
In this electrostatic approach we solve Laplace equation
In the case of an homogeneous, isotropic sphere
this leads to general solutions
where Pl
(cos θ) are Legendre Polynomials of
order l. The coefficients Al
and Bl
can be
determined from the boundary conditions.
John William Strutt,
3rd
Baron Rayleigh

6. Quasistatic Approximation
Rayleigh theory
Boundary conditions at the surface of the NP implies
continuity of E∥
continuity of D⊥
which leads to
The distribution of electric field inside and outside the sphere are
evaluated from the potentials

7. Polarizability in Quasistatic Approximation
where we introduced the dipole moment
Using p=ε0
εm
αE0
we obtain the polarizability of a subwavelength
sphere in the quasistatic approximation
(Clausius-Mossotti relation)
Polarizability of a silver
NP where ε is described
by a Drude model

8. Polarizability in Quasistatic Approximation
The polarizability experiences a resonant
enhancement when |ε + 2εm
| is minimum which simplifies to
Re{ε(ω)}=−2εm
(Fröhlich condition)
for small or slow-varying Im{ε}.
For a Drude sphere in air, this criterion
is met at frequency
, for the dipole (l=1)
Reminder: Resonance conditions
Bulk: ε(ω) = 0 at ωp
Surface: Re{ε(ω)}=−εm
at ωp
/√2 Rakić, Appl. Opt. 1995, 34, 4755
Rakić, Appl. Opt. 1995, 34, 4755
Al
Surface
Bulk
Sphere in air
ε”
ε’

9. Optical Cross-Sections
Poynting vector for a plane wave incident on a small Al sphere:
On resonance
(8.8 eV)
Off resonance
(5 eV)
Bohren and Huffman, Absorption and Scattering of Light by Small Particles, Wiley
Interscience, 1983
A particle can absorb light from
a much larger region than its
geometrical size (red dashed
circle): absorption cross-section.
Similar definitions hold for
scattering and extinction.

10. Optical Cross-Sections in Quasistatic
Approximation
The scattering cross-section of the sphere is obtained by dividing
the total radiated power of the sphere’s dipole by the intensity of
the incident field:
The Poynting theorem leads to the absorption cross-section
The extinction cross-section, which corresponds to the total power
removed from the incident field, is simply
Important: Csca
scales as a6
while Cabs
scales as a3
. This means that
absorption will be dominant in small NPs while the scattering will
dominate in large NPs.

11. 20 nm
Ag NP
in air
60 nm
Ag NP
in air
Optical Cross-Sections in Quasistatic
Approximation
50 nm
Au NP
in air
150 nm
Au NP
in air
The transition between the two regimes is characterized
by a distinct color change

12. Famous Examples
Lycurgus Cup (4th
century)
British Museum, London
Stained Glass,
South Rose Window (1260)
Notre Dame, Paris

13. Famous Example – Lycurgus Cup
Au NP in glass has scattering & absorption.
Transmission: the absorption component
allows only the large wavelengths (>600
nm) to be transmitted ▶ red
Reflection: the scattering component
dominates, allowing the NP resonant
wavelength to be observed ▶ green
50 nm
Au NPs
in glass

14. Mie and Gans Theories
The quasistatic approximation is valid and justified for NP below
100 nm in size. For larger NPs, phase-changes of the incident field
over the NP volume become significant
▶ Rigorous electrodynamic approach needed
Solution of Maxwell’s equations for
●
Spherical particles: Mie theory
Mie, Ann. Phys. Vierte Folge 1908, 25, 377
●
Ellipsoidal particles: Gans theory
Gans, Ann. Phys. 1912, 342, 881
NB: Gans (a.k.a. Mie-Gans) theory is an expansion of Mie theory
and requires the adoption of the quasistatic approximation.
Gustav Mie Richard Gans

15. Mie Theory
Mie theory is an analytic method for solving
limited cases of the scattering problem:
●
Spherically symmetric particles only
●
Homogeneous and isotropic materials
●
For planar incident waves
Extensions of Mie theory:
●
Concentric spheres
●
Ensemble of spheres
●
Ellipsoids (Gans theory)
●
Cylinders
Gustav Mie

16. Mie Theory
Thanks to the symmetry of the system, the problem is reduced to
solving
Solutions can be constructed from linear combination of even and
odd generating functions
The E and H fields can be expressed as
where are vector harmonics
satisfying the wave equation and u and v are solutions of the
scalar wave equation.
Legendre polynomials Bessel functions

17. Mie Theory
Outside Mie solution, scattered wave:
Inside Mie solution:
The Mie coefficients al
, bl
, cl
, and dl
can be derived after some long
algebra.
Legendre polynomials
Spherical Hankel functions
Spherical Bessel functions

18. Mie Theory
Mie scattering coefficients Mie coefficients for inside fields:
(outside the sphere):
where is the relative refractive index,
and are the Riccatti-Bessel functions.

19. Mie Theory
Once the Mie scattering coefficients are determined we can
calculate the scattering, absorption, and extinction cross-sections
Au: 150 nm, in water Ag: 150 nm, in water Al: 150 nm, in water

20. + ‑
‑ +
Beyond the Quasistatic Approximation
The quasistatic approximation breaks down for two regimes:
●
Large sizes (>100 nm)
▶ Retardation effects: Finite speed of light, phase-change
Leads to spectral red-shift of LSP modes and excitation of high
order dark modes (multipoles).
▶ Increase of radiation damping: ↗Scattering
●
Very small sizes (< 10 nm)
▶ Surface scattering: NP size ~ electron mean free path
Leads to spectral broadening of the LSP modes
(i.e., decrease of plasmon lifetime)
+
‑

21. Ag sphere from 10 to 300 nm
Beyond the Quasistatic Approximation

22. Beyond the Quasistatic Approximation
Ag
10 nm
Ag
50 nm
Ag
100 nm
Ag
200 nm
Ag
150 nm
Ag
120 nm
Spectral red-shift and radiative broadening of LSPs,
excitation of high order LSP modes

23. Dipole
l=1
Octupole
l=4
Hexapole
l=3
Quadrupole
l=2
Multipoles
Ei
ki
Al
150 nm
water

24. Dipole vs Quadrupole
Dipole
l=1
Quadrupole
l=2

25. Beyond Mie Theory
Mie Theory is limited to simple cases (spherical particle).
▶ What about more complex geometries (real NPs are always
spherical)?
Electrodynamic numerical simulations are required to solve
Maxwell’s equation in complex geometries!
FDTD, FEM/FEA, DDA, BEM, DGTD, Green formalism, MM, MoM,…
(cf. Chapter 7)

26. Beyond Mie Theory
These numerical methods are:
●
Full-wave methods: solve the complete set of Maxwell’s
equations w/out any simplifying assumptions
●
Fully retarded: retardation effects, radiation
damping, phase change are account for
●
Able to handle (virtually) any
geometry and configuration

27. Plasmon Energy – Shape Dependence
Surface:
Sphere:
Bulk:
Cavity:
The plasmon
energies of a metal
nanoparticle depend
on its shape!

28. Plasmon Hybridization
Similarly to atomic states hybridize to form bonding and
antibonding molecular orbitals (bonds), Plasmon modes
hybridize to form bonding and antibonding hybridized
plasmon modes
▶ Plasmon Hybridization Theory (Peter Nordlander, 2003)
The energy depends on
the aspect ratio x.
Nordlander et al.,
Science 2003, 302, 419
JCP 2003, 120, 5444
Nano Lett. 2004, 4, 899
JCP 2006, 125, 124708

29. Plasmon Hybridization
PH applies to any system:
Core-Shell NP Dimer of spheres Dimer of nanorods
The same PH diagrams can be shown for
other modes (quadrupole,...)

30. Plasmon Hybridization
In a dimer of NPs, PH provides the energy of the hybridized modes
as a function of the NP separation distance (gap).
▶ The closer the NPs, the stronger the interaction, the
stronger the hybridization
Zhang et al, ACS Nano 2015, 9, 9331

31. Plasmon Interactions
NP chains NP clusters NP oligomers
Lassiter et al.,
Nano Lett. 2012, 12, 1058
Slaughter et al.,
Nanoscale 2014, 6, 11451
Urban et al.,
Nano Lett. 2013, 13, 4399

32. Spectral Tunability of the LSPR
Nanoshell Nanorod Dimer
Romero et al., Opt.
Express 2006, 14, 9988
Chen et al., Plasmonics
2012, 7, 509
El-Sayed et al., J. Adv.
Res. 2010, 1, 13

33. Spectral Tunability of the LSPR
Plasmon energy (eV)
8 … 3.5 3.0 2.5 2.0 1.5 1.0 0.5
150 … 400 500 600 800 1000 3000 9000
Wavelength (nm)
UV | Visible | Near-IR | Mid-IR
Ag nanospheres
Au nanospheres
Nanoshells, nanoeggs
Nanorods
Nanoprisms, triangles
Nanocubes
Nanorice
Al nanospheres
Graphene

34. Near-Field Enhancement
The NP size, shape, and arrangement strongly influence local
electric field distribution and intensity near the NP surfaces.
▶ Localization & Enhancement
Zhang et al., ACS Appl. Mater. Interfaces 2014, 6, 17255
Schlather et al.,
Nano Lett. 2013,
13, 3281
Chien et al.,
Opt. Express 2008,
16, 1820

35. Near-Field Enhancement
Extremely large NF enhancement in gaps
Romero et al., Opt. Express 2006, 14, 9988
+
‑ +
‑
+
‑ +
‑
+
‑ +
‑
+
‑ +
‑

36. Near-Field Imaging of the LSP
Optical near-field imaging of plasmon fields (amplitude & phase):
30 nm resolution
Schnell et al., Nat. Photonics. 2009, 3, 287
Hillenbrand et al.,
Appl. Phys. Lett., 2003, 83, 368

37. Near-Field Imaging by the LSP
Near-Field Optical Microscopy w/ plasmonic nanoantenna probes
▶ Use of plasmon-induced near-field (cf. Chapter 3)

38. Environment Effects
When a NP is placed in a homogeneous dielectric environment
(εm
≠1): LSPR spectral shift ▶ Dielectric Screening
NB: Key effect for LSPR sensing
(cf. Chapter 11)
Link et al., J. Phys. Chem. B 1999, 103, 3073
+
+ +
ε(ω)
‑ ‑
‑
‑
‑ ‑
+ +
+ εm
Ei
ki

39. Environment Effects
When a NP is placed near a dielectric substrate (εs
≠1):
●
LSPR spectral shift
●
Degeneracy of the LSP modes lifted
●
Higher order LSP modes enhanced
▶ Image Charge
Knight et al., Nano Lett. 2009, 9, 2188
Lermé et al., J. Phys. Chem. C 2013, 117, 6383
+
+ +
‑ ‑
‑
Ei
ki
+
+ +
‑ ‑
‑ εs
‑ +
‑ +
‑ +
Ei
ki
+ ‑
+ ‑
+ ‑

40. Bipyramids
Lee et al,
Chem. Commun. 2015, 51, 15494
Martinsson et al,
Small 12, 1613 (2016)
Prisms
Lofton et al.
Adv. Func. Mater. 2005
Pyramids
Im et al.
Angew. Chem. Int. Ed. 2005, 44
Cuboids/Bars
Porous NPs
Zhang et al,
JPC Lett. 2014, 5, 370
Playing with Shapes – Bottom-Up Approach
Halas et al. Rice University
NanoRice
Sun et al.
J. Am. Chem. Soc. 126 (2004)
NanoCages
Trisoctahedra
Zhang et al,
ACS Applied Materials
Interfaces 6, 17255 (2014)
Triangular Frames
Shahjamali et al,
Small 9, 2880 (2013)
Platelets
McEachran et al,
Chem. Commun., 2008,
573
Cubes
Martinsson et al,
Small 12, 1613 (2016)
Das et al,
Nanotechnology
2014, 24, 405704
Stars
Rods
Martinsson et al,
Small 2016, 12, 1613
Spheres
Zhang et al,
JPC Lett. 2014, 5, 370

41. Playing with Shapes – Top-Down Approach
Large et al,
Opt. Express 2011, 19, 5587
Lin et al, Adv. Mater. 2012, 24
Zhou et al,
Int. J. Nanomedicine 2011
Massango et al,
Nano Lett. 2016, 16, 4251
Zhang et al,
ACS Nano 2015, 9, 9331
Kolkowski et al, ACS Photonics 2015
Liu et al, ACS Nano 2012, 6, 5482
Gottheim et al,
ACS Nano 2015, 9, 3284
Day et al,
Nano Lett. 2015, 15, 1324

42. Key points
●
Localized Surface Plasmon (LSP)
●
Scattering Problem
●
Rayleigh Theory, Quasistatic Approximation
– Polarizability of a sphere, Clausius-Mossotti relation
– Fröhlich (resonance) condition
– Optical cross-sections: scattering, absorption, extinction
●
Mie Theory
– Electrodynamic approach for spheres
– Mie scattering coefficients
– Retardation effects, Surface scattering
●
Gans Theory
– Polarizability of an ellipsoid
●
Beyond Mie Theory
– Real particles
– Electrodynamic methods (cf. Chapter 7)
●
Plasmon Hybridization
– Spectral tunability
– Near-field localization & enhancement, Plasmon imaging
– Environment effects: dielectric screening, image charge