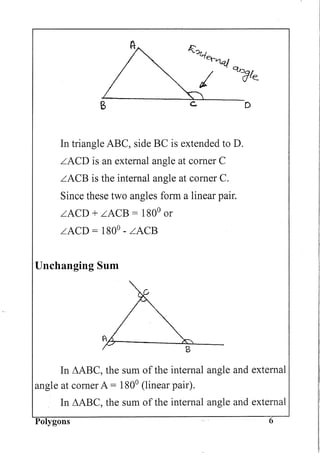
This document is a mathematics textbook for 8th standard students. It covers two chapters: equations and polygons. The equations chapter discusses addition, subtraction, multiplication, and division of numbers and solving problems using algebraic methods. The polygons chapter defines polygons as shapes with three or more sides. It discusses the sum of interior angles in polygons, exterior angles, how the sum of interior and exterior angles is always 180 degrees, and defines regular polygons as those with all equal sides and angles.

1. MATHE MATICS
Std. VIII
A TEXT BOOK OF
MATHEMATICS
STD : VIII

2. MATHEMATICS
DIGITAL TEXT BOOK
Std. VIII
Anchulekshmi A R
B.Ed Mathematics
Reg.No. 18014350002

3. CONTENTS
Chapter I
Equations
1. Addition and Subtraction
2. Multiplication and Division
3. Method ofAlgebra
4. Different Problems
1. Polygons
Chapter II
Polygons
2. Sum of the angles
3. External angles
4. Unchanging sum
5. Regular Polygons

4. Chapter 1
EQUATIONS
Equations are algebraic sentences denoting equality
of numbers
Addition and Subtraction
i. Addition of numbers
Eg: 40 + 3 = 43
50 + 3 = 53
H. Subtraction of Numbers
Eg: 40 - 3 = 37
50 - 3 = 47
Problems related to Addition and Subtraction of Numbers
Eg: Rajan said "if 6 more marks were granted. My
marks in Maths would be 100." Howmany marks
did he get?
Ans : It will become 100 if 6 more added. So his marks is
6 less than 100.
100 - 6 = 94. This is Rajans Marks.
Equations 1

5. Multiplication and Division
i. Multiplication of Numbers
Eg: 40 x 3 = 120
22 x 3 = 66
ii. Division of Numbers
Eg: 125 + 5 = 25
42+2=21
Problems related to Multiplication and Division of
Numbers
Eg: A number multiplied by 12 gIves 756. Which
number was multiplied?
Ans: 756 + 12 = 63
Method of Algebra
It is easy to solve all the problems of numbers using
algebra.
The unknown number or variable ofthe equation is x.
Then to find x, in all cases we used the method of inverse
operation in charge subtraction to addition, change
Equations 2

6. ... multiplication to division and change division to
~.
tnlltiplication.
The formulas are
if x+a= b, x =b - a
if x-a = b, x=b+a
b
if ax=b X= -, a
if ~=b , x=bxa
a
if ax+b = c, ax = c-b
c-b
x=--
a
To Recollect
x + x = 2x
x + 2x = 3x
2x + 3x = 5x
5x - x = 4x
2x - x = x
7x - 5x = 2x
2x + 1 = 2x + 1 it self
Equations 3

7. Different Problems
Eg: When 10 was added to 2 times a number, we get 4
times the number. What is the number?
Ans: Let the number be x
2x+10 = 4x
There is variable on both sides ofthe equal to. sign in
this equation.
Subtract 2x from both sides of the equal to sign
Equations
2x + 10 - 2x = 4x - 2x
10 = 2x
2x = 10
10
x=-=5
2
4

8. Chapter 2
POLYGONS
Polygons is the common name given to shapes with
three or more sides.
Eg:6D
Sum of the Angles
The sum ofthe angles of a polygon of n sides is
(n-2) x 1800
The sum of the angles of a polygon is always a
multiple of 180.
Eg: What is the sum ofthe angles ofa polygon of52 sides.
Ans : Sum ofthe angles
= (n-2) x 1800
= (52 - 2) x 1800
=50x180
= 90000
External Angles
If one side of a triangle is extended. We get an exter-
nal.angle.
Polygons 5

9. Co
In triangle ABC, side BC is extended to D.
LACD is an external angle at corner C
LACB is the internal angle at corner C.
Since these two angles form a linear pair.
LACD + LACB = 1800
or
LACD = 1800
- LACB
Unchanging Sum
D
In i1ABC, the sum of the internal angle and external
angle at corner A = 1800
(linear pair).
In i1ABC, the sum of the internal angle and external
Polygons 6

10. angle at comer B = 1800
(Linear pair)
In L1ABC, the sum of the internal angle and external
angle at comer C = 1800
(linear pair)
Sum of the three internal angles and three external
angles of L1ABC = 180x3 = 5400
But sum ofthe internal angles = 1800
So sum of the angles external
= 540 - 180 = 3600
In any triangle, the sum ofthe external
angles is 360°.
Now let us examine the case in a quadrilateral.
Sum of the internal angle and external angle at
A = 1800
Sum of the internal angle and external angle at all
four corners = 180 x 4 = 7200
A ------L....LJ
B
Polygons 7

11. But sum of the internal angles of a quadrilateral is
360°.
So sum ofthe external angles of a quadrilateral
= 720 - 360
= 360°
In the same way examine the sum ofthe external angles
of a pentagon, hexagone, etc. Always we get it as 360°.
Sum ofthe external angles ofany
polygon is 360°.
Eg: The angles of 18 sided polygon are equal. What is the
measure of each external angle?
Ans: Sum ofthe external angles ofthe polygon with
18 sides = 360°.
Since the angles are equal, external angles are
also equal.
Measure of each external angle = 360 = 200
18
Regular Polygons
Polygons with all sides equal and all angles equal are
called regular polygons.
Polygons 8

12. MATHE MATICS
Std. VIII
A TEXT BOOK OF
MATHEMATICS
STD : VIII