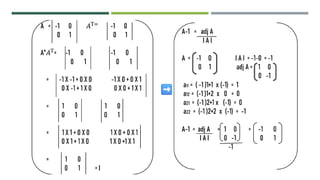
The document discusses orthogonal matrices, defining their properties and significance in various applications such as computer graphics, signal processing, and quantum mechanics. It explains that the product of two orthogonal matrices is also orthogonal, and emphasizes that their transpose is equal to their inverse. The document covers the mathematical qualities and uses of orthogonal matrices in representing transformations.

1. PRODUCT OF TWO ORTHOGONAL MATRICES AND ITS INVERSE, DESCRIBE THE MEAN OF
ROTATION
DIFFERENTIAL EQUATION AND LINEAR ALGEBRA
 DISHA AGARWALLA
(230301120281)
 KONCHADA BHARGAVI
(230301120289)
 SHRABANEE ROUTRAY
(230301120295)
PRESENTED BY:
B.TECH(CSE)
SEC-F
Guided by:
Dr. Swarnalata Jena

2. CONTENTS:
 ORTHOGONALMATRIX
 PRODUCTOFTWOORTHOGONAL MATRIX
 INVERSEOFORTHOGONALMATRIX
 MEANOFROTATION

3. ORTHOGONAL MATRIX:
 We know that a square matrix has an equal number of rows and columns.
 A square matrix with real numbers or elements is said to be an orthogonal matrix, if its transpose is equal to its
inverse matrix.
DEFINITION:
When the product of a square matrix and its transpose gives an identity matrix, then the square matrix is known as an
orthogonal matrix .
Suppose A is a square matrix with real elements and of n x n order and AT is the transpose of A. Then
according to the definition, if, AT = A-1 is satisfied, then, AAT = I Where ‘I’ is the identity matrix, A-1 is the inverse
of matrix A, and ‘n’ denotes the number of rows and columns

4. PROPERTIES:
•Orthogonal matrices preserve vector lengths, angles, and distances under multiplication.
•The transpose of an orthogonal matrix is its inverse.
•The determinant of an orthogonal matrix is either 1 or -1.
•Orthogonal matrices are used in various applications including rotation, reflection, and scaling
transformations.

5. APPLICATIONS:
•Computer graphics:
Orthogonal matrices are commonly used to represent 3D rotations and
transformations in computer graphics and gaming.
•Signal processing:
Orthogonal matrices play a crucial role in signal processing applications
such as image compression and filtering.
•Quantum mechanics:
In quantum mechanics, orthogonal matrices are used to represent unitary
transformations that preserve probabilities.

6. ORTHOGONAL MATRIX:

8. PRODUCTOFTWOORTHOGONALMATRIX:

10. INVERSEOFORTHOGONALMATRIX:
 We know that the product of two orthogonal matrix is a orthogonal matrix then we find its inverse then
its inverse is a orthogonal matrix as per the formula.
 A.𝐴T
= 𝐴−1
. A = I
 ⇒ 𝐴−1
= 𝐴T

11. THANK YOU!