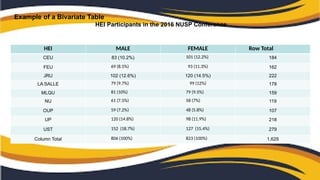
The document outlines various statistical techniques and methodologies for analyzing performance outcomes, emphasizing the importance of descriptive and inferential statistics. It covers types of data analysis, including univariate, bivariate, and multivariate analysis, along with methods like correlation, regression, and ANOVA. The document also explains key measures, such as correlation coefficients and hypothesis testing, to interpret relationships between variables.

1. Different Statistical Techniques

2. Life Performance
Outcomes
I am Courageous, Resourceful
EXPLORERS & PROBLEM
SOLVERS

3. Essential Performance
Outcomes
Seek out issues, possibilities, and
sources of related information
willingly for further investigation and
development.

4. Intended Learning
Outcomes
Seek out issues, possibilities, and sources
of related information using different
statistical techniques for further
investigation and development.

5. Statistics - is a term that pertains to your acts of collecting and
analyzing numerical data.
 Doing statistics then means performing some arithmetic procedures
like addition, division, subtraction, multiplication, and other
mathematical calculations.
 Statistics involves analysis, planning, interpreting, and organizing
data in relation to the design of the experimental method you chose.
 Statistical methods then are ways of gathering, analyzing, and
interpreting variable or fluctuating numerical data.

6. Statistical Methodologies
1. Descriptive Statistics
 This describes a certain aspect of a data set by making you
calculate the Mean, Median, Mode and Standard Deviation.
 It tells about the placement or position of one data item in relation to
the other data, the extent of the distribution or spreading out of data,
and whether they are correlations or regressions between or among
variables. This kind of statistics does not tell anything about the
population.

7. Statistical Methodologies
2. Inferential Statistics
 It is a branch of statistics that focuses on conclusions,
generalizations, predictions, interpretations, hypotheses, and the
like.
 There are a lot of hypotheses testing in this method of statistics that
require you to perform complex and advanced mathematical
operations.

8. Types of Statistical Data Analysis
Univariate Analysis – analysis of one variable
Bivariate Analysis – analysis of two variables (independent
and dependent variables)
Multivariate Analysis – analysis of multiple relations between
multiple variables.

9. Statistical Methods of Bivariate Analysis
1. Correlation or Covariation (correlated variation)
 Describes the relationship between two variables and
also tests the strength or significance of their linear
relation.
This is a relationship that makes both variables getting the
same high score or one getting a higher score and the
other one, a lower score.

10. Statistical Methods of Bivariate Analysis
 Covariance is the statistical term to measure the extent of the
change in the relationship of two random variables.
 Random variables are data with varied values like those ones in the
interval level or scale (strongly disagree, disagree, neutral, agree,
strongly agree) whose values depend on the arbitrariness or
subjectivity of the respondent.

11. Statistical Methods of Bivariate Analysis
2. Cross Tabulation
 Also called “crosstab or students-contingency table” that follows the
format of a matrix (plural: matrices) that is made up of lines of numbers,
symbols, and other expressions.
 By displaying the frequency and percentage distribution of data, a
crosstab explains the reason behind the relationship of two variables and
the effect of one variable on the other variable.
 If the table compares data on only two variables, such table is called
Bivariate Table.

12. Example of a Bivariate Table
HEI Participants in the 2016 NUSP Conference
HEI MALE FEMALE Row Total
CEU 83 (10.2%) 101 (12.2%) 184
FEU 69 (8.5%) 93 (11.3%) 162
JRU 102 (12.6%) 120 (14.5%) 222
LA SALLE 79 (9.7%) 99 (12%) 178
MLQU 81 (10%) 79 (9.5%) 159
NU 61 (7.5%) 58 (7%) 119
OUP 59 (7.2%) 48 (5.8%) 107
UP 120 (14.8%) 98 (11.9%) 218
UST 152 (18.7%) 127 (15.4%) 279
Column Total 806 (100%) 823 (100%) 1,629

13. Measure of Correlation
1. Correlation Coefficient
• This is a measure of the strength and direction of the linear
relationship between variables and likewise gives the extent of
dependence between two variables; meaning, the effect of one
variable on the other variable.
 Spearman’s rho– the test to measure the dependence of the
dependent variable on the independent variable

14. 1. Correlation Coefficient
 Pearson product-moment correlation – measures the strength and
direction of the linear relationship of two variables and of the association
between interval and ordinal variables.
 Chi-square – is the statistical test for bivariate analysis of nominal
variables, specifically, to test the null hypothesis. It tests whether or not a
relationship exists between or among variables and tells the probability
that the relationship is caused by chance. This cannot in any way show
the extent of the association between two variables.

15. 1. Correlation Coefficient
 t-test – evaluates the probability that the mean of the sample reflects the mean
of the population from where the sample was drawn. It also tests the difference
between two means: the sample mean and the population mean. ANOVA or
analysis of variance also uses t-test to determine the variance or the difference
between the predicted number of the sample and the actual measurement.

16. Types of ANOVA
a. One-way analysis of variance – study of the effects of the
independent variable
b. ANCOVA (Analysis of Covariation) – study of two or more
dependent variables that are correlated with one another
c. MANCOVA (Multiple Analysis of Covariation) – multiple analyses of
one or more independent variables and one dependent variable to
see if the independent variables affect one another.

17. Measure of Correlation
2. Regression
 Similar to correlation, regression determines the existence of variable
relationships, but does more than this by determining the following:
1) which between the independent and dependent variable can signal
the presence of another variable
2) how strong the relationship between the two variables are
3) when an independent variable is statistically significant as a
soothsayer or predictor.