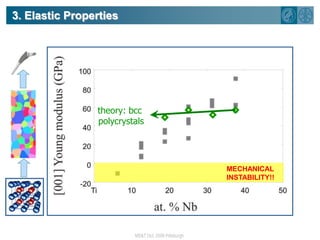
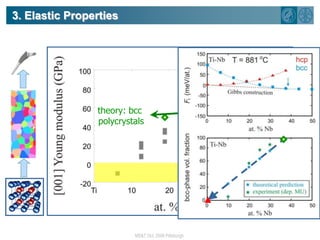
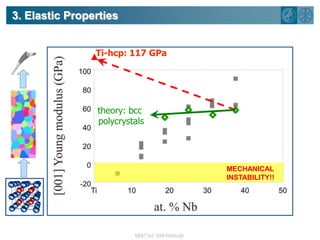
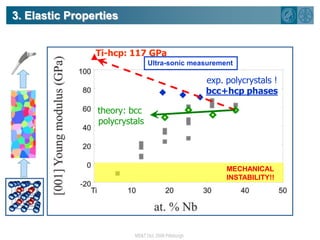
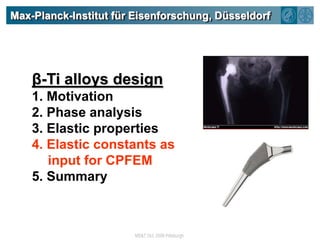
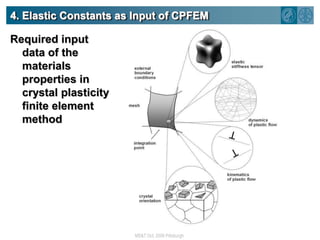
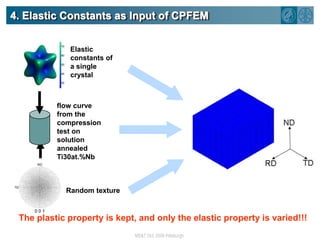
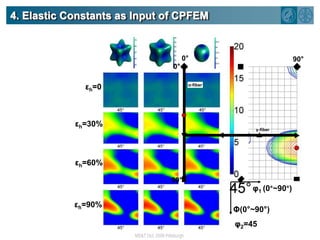
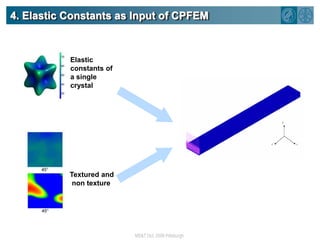
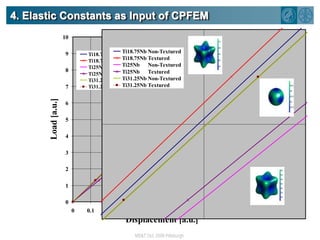
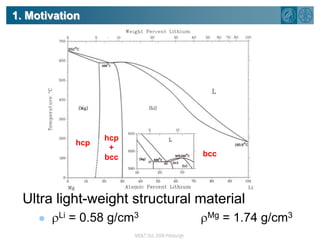
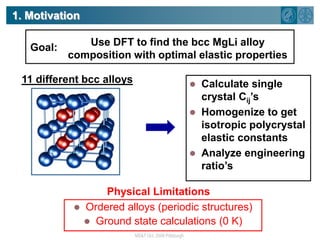
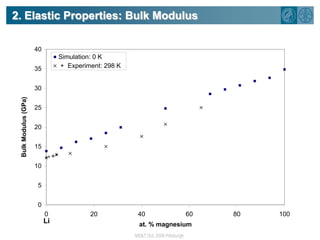
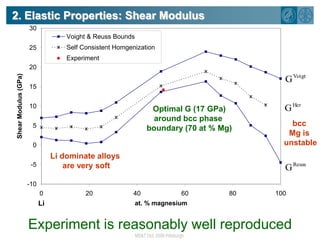
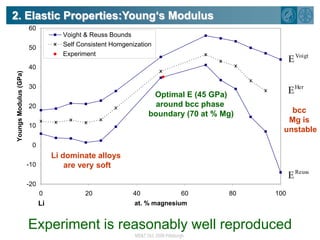
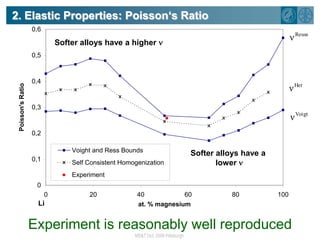
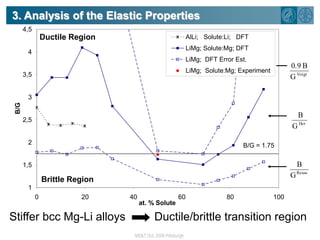
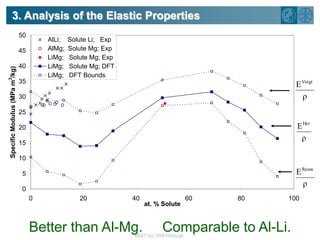
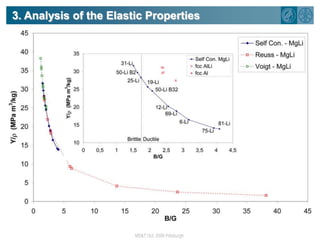
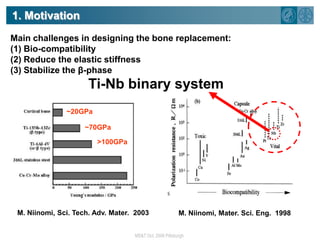
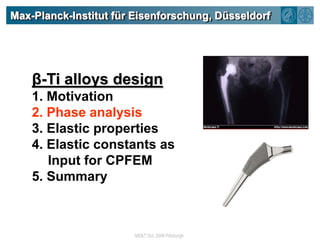
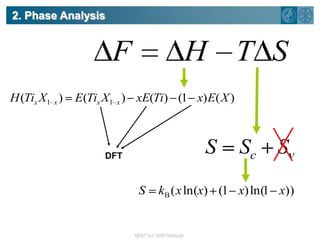
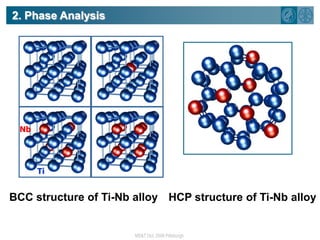
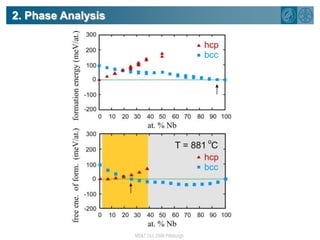
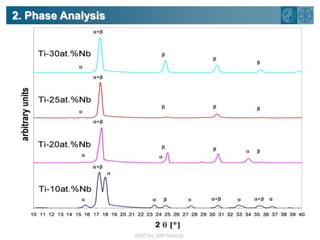
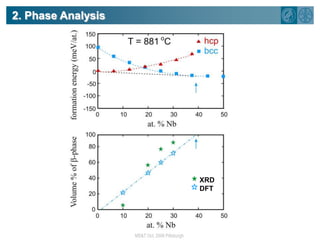
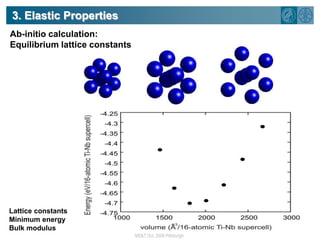
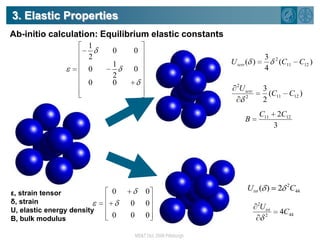
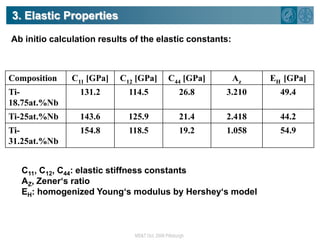
The document summarizes research on using density functional theory (DFT) coupled with continuum mechanics to design new alloys. It presents two examples: designing β-titanium alloys for implants by stabilizing the softer β-phase using niobium additions, and designing magnesium-lithium alloys for lightweight structures by stabilizing the bcc crystal structure. For the titanium alloys, DFT is used to analyze phases, calculate elastic properties, and determine that niobium additions stabilize the β-phase and make the alloys softer and more compatible for implants. For the magnesium alloys, DFT calculates the elastic properties of bcc magnesium-lithium alloys to identify compositions with optimal stiffness,

1. Max-Planck-Institut für Eisenforschung, DüsseldorfCoupling Density Functional Theory with Continuum Mechanics forAlloy DesignD. Ma*, M. Friák, W. Counts, D. Raabe, J. NeugebauerMax Planck Institute for Iron Research, Düsseldorf, Germany

2. Max-Planck-Institut für Eisenforschung, DüsseldorfMulti-scale ModelingmmμmnmÅ

3. Max-Planck-Institut für Eisenforschung, DüsseldorfMulti-scale ModelingmmmmÅμmnmÅ

4. Max-Planck-Institut für Eisenforschung, DüsseldorfTwo Examples:(1) β-Ti Alloys for implants(2) Mg-Li Alloys for lightweight structures

5. Max-Planck-Institut für Eisenforschung, Düsseldorfβ-Ti alloy design1. Motivation2. Phase analysis3. Elastic properties4. Elastic constants as input for CPFEM5. Summary

6. Max-Planck-Institut für Eisenforschung, Düsseldorfβ-Ti alloys design1. Motivation2. Phase analysis3. Elastic properties4. Elastic constants as Input for CPFEM5. Summary

7. 1. Motivation

8. 1. MotivationMain challenges in designing the bone replacement:(1) Bio-compatibility(2) Reduce the elastic stiffness(3) Stabilize the β-phaseTi-Nb binary system~20GPa~70GPa>100GPaM. Niinomi, Sci. Tech. Adv. Mater. 2003M. Niinomi, Mater. Sci. Eng. 1998

9. Max-Planck-Institut für Eisenforschung, Düsseldorfβ-Ti alloys design1. Motivation2. Phase analysis3. Elastic properties4. Elastic constants as Input for CPFEM5. Summary

10. 2. Phase AnalysisDFT

11. NbTiunwanted hcp-based phasethat is stiffer and stable2. Phase Analysiswanted bcc-based phase that is softer but metastableBCC structure of Ti-Nb alloyHCP structure of Ti-Nb alloy

12. 2. Phase Analysis

13. 2. Phase Analysis

14. 2. Phase AnalysisXRDDFT

15. Max-Planck-Institut für Eisenforschung, Düsseldorfβ-Ti alloys design1. Motivation2. Phase analysis3. Elastic properties4. Elastic constants as Input for CPFEM5. Summary

16. 3. Elastic PropertiesAb-initio calculation:Equilibrium lattice constantsLattice constantsMinimum energyBulk modulus

17. 3. Elastic PropertiesAb-initio calculation: Equilibrium elastic constantsε, strain tensorδ, strainU, elastic energy densityB, bulk modulus

18. 3. Elastic PropertiesAb initio calculation results of the elastic constants:C11, C12, C44: elastic stiffness constantsAZ, Zener‘s ratioEH: homogenized Young‘s modulus by Hershey‘s model

19. 3. Elastic PropertiesYoung‘s modulus surface plotsPure NbTi-25at.%NbTi-31.25at.%NbTi-18.75at.%Nb[001][100][010]Az=3.210Az=1.058Az=0.5027Az=2.418 The elastic properties of the Ti-Nb binary alloys become isotropic as the Nb content increases

20. 3. Elastic Properties

21. single-crystallineC11, C12, C44, B0micro-scalemacro-scalepolycrystallineYoung modulus3. Elastic Properties64μ H4 + 16(4C11 + 5C12)μ H3 + [3(C11+ 2C12) × (5C11+ 4C12) -8(7C11 – 4C12)C44]μ H2-(29C11 – 20C12)(C11+2C12)C44 μ H–3(C11 + 2C12)2(C11 – C12)C44 = 0 “scale-jumping”(across the meso-scale)

22. 3. Elastic Propertiestheory: bcc polycrystalsMECHANICALINSTABILITY!!

23. 3. Elastic Propertiestheory: bcc polycrystalsMECHANICALINSTABILITY!!

24. 3. Elastic PropertiesTi-hcp: 117 GPatheory: bcc polycrystalsMECHANICALINSTABILITY!!

25. Ultra-sonic measurementexp. polycrystals !bcc+hcp phases3. Elastic PropertiesTi-hcp: 117 GPatheory: bcc polycrystalsMECHANICALINSTABILITY!!

26. Max-Planck-Institut für Eisenforschung, Düsseldorfβ-Ti alloys design1. Motivation2. Phase analysis3. Elastic properties4. Elastic constants as input for CPFEM5. Summary

27. 4. Elastic Constants as Input of CPFEMRequired input data of the materials properties in crystal plasticity finite element method

28. 4. Elastic Constants as Input of CPFEM Plane strain compression: (1) Influence of the elastic anistropy (2) predict the texture evolution Bending test: Homogenized elastic properties of textured and non-texture materials

29. 4. Elastic Constants as Input of CPFEM Elastic constants of a single crystal flow curve from the compression test on solution annealed Ti30at.%NbRandom textureThe plastic property is kept, and only the elastic property is varied!!!

30. 4. Elastic Constants as Input of CPFEM0°90°0°εh=0α-fiberεh=30%γ-fiberεh=60%90°φ1 (0°~90°)εh=90%Φ(0°~90°)φ2=45°

31. 4. Elastic Constants as Input of CPFEM Elastic constants of a single crystal Textured and non texture

32. 4. Elastic Constants as Input of CPFEM

33. Max-Planck-Institut für Eisenforschung, Düsseldorfβ-Ti alloys design1. Motivation2. Phase analysis3. Elastic properties4. Elastic Constants as Input of CPFEM5. Summary

34. 5. SummaryThermodynamic stability of hcp- and bcc-Ti was studiedConfigurational entropy at finite temperature stabilizes bcc Ti-NbphaseVolume fractions have been calculated using the Gibbs construction Polycrystalline two-phase Young’s modulus has been theoretically predicted employing the Hershey and CPFEM homogenization methods Very good agreement between theoretical prediction and experimentThe calculated elastic constants (DFT) can be used as input for CPFEM Nb SHOULD BE THE PRIMARY ALLOYING ELEMENTS IN Ti FOR HUMAN IMPLANT MATERIALS

35. Max-Planck-Institut für Eisenforschung, DüsseldorfMg-Li alloy design1. Motivation2. Elastic properties3. Analysis of the Elastic Properties4. Summary

36. Max-Planck-Institut für Eisenforschung, DüsseldorfMg-Li alloy design1. Motivation2. Elastic properties3. Analysis of the Elastic Properties4. Summary

37. 1. MotivationMagnesium BadMagnesium Good Magnesium (and its alloys) are generally hcp

38. Not ductile, textures

39. Problematic for industrial applications (anisotropy)

40. Magnesium (and its alloys) are light weight and relatively strong

41. Ideal lightweight structural materialHow can hcp magnesium be transformed into bcc/fcc magnesium?

42. 1. Motivationhcp+bcchcpbccUltra light-weight structural materialrLi = 0.58 g/cm3rMg = 1.74 g/cm31. MotivationUse DFT to find the bcc MgLi alloy composition with optimal elastic propertiesGoal:11 different bcc alloysCalculate single crystal Cij’s

43. Homogenize to get isotropic polycrystal elastic constants

44. Analyze engineering ratio’sPhysical LimitationsOrdered alloys (periodic structures)

45. Ground state calculations (0 K)Max-Planck-Institut für Eisenforschung, DüsseldorfMg-Li alloy design1. Motivation2. Elastic properties3. Analysis of the elastic Properties4. Summary

46. 2. Elastic Properties: Bulk ModulusLi

47. 2. Elastic Properties: Shear ModulusOptimal G (17 GPa)around bcc phase boundary (70 at % Mg)bcc Mg is unstableLi dominate alloys are very softLiExperiment is reasonably well reproduced

48. 2. Elastic Properties:Young‘s ModulusOptimal E (45 GPa)around bcc phase boundary (70 at % Mg)bcc Mg is unstableLi dominate alloys are very softLiExperiment is reasonably well reproduced

49. 2. Elastic Properties: Poisson‘s RatioSofter alloys have a higher nSofter alloys have a lower nLiExperiment is reasonably well reproduced

50. Max-Planck-Institut für Eisenforschung, DüsseldorfMg-Li alloy design1. Motivation2. Elastic properties3. Analysis of the elastic Properties4. Summary

51. 3. Analysis of the Elastic PropertiesDefined as

52. Based on experimental observations

53. Measure of ductile vs. brittle behaviorG Resisting Plastic FlowB Bond StrengthOppositionTo Fracture1.75 critical value