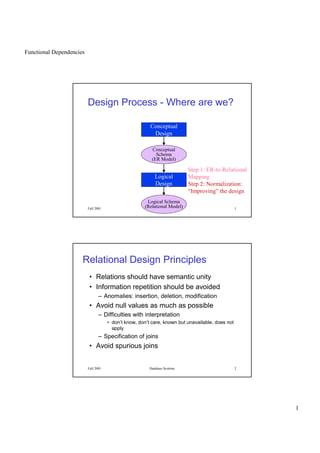
The document discusses the design process of database systems, focusing on the importance of normalization to avoid anomalies such as update, insertion, and deletion anomalies. It explains key concepts including functional dependencies, superkeys, candidate keys, and the necessary conditions for lossless decomposition and functional dependency preservation. The document also outlines normalization forms and the criteria for achieving Boyce-Codd Normal Form (BCNF).

1. Functional Dependencies
1
Fall 2001 Database Systems 1
Design Process - Where are we?
Conceptual
Design
Conceptual
Schema
(ER Model)
Logical
Design
Logical Schema
(Relational Model)
Step 1: ER-to-Relational
Mapping
Step 2: Normalization:
“Improving” the design
Fall 2001 Database Systems 2
• Relations should have semantic unity
• Information repetition should be avoided
– Anomalies: insertion, deletion, modification
• Avoid null values as much as possible
– Difficulties with interpretation
• don’t know, don’t care, known but unavailable, does not
apply
– Specification of joins
• Avoid spurious joins
Relational Design Principles

2. Functional Dependencies
2
Fall 2001 Database Systems 3
Normalization
• A bad database design may suffer from anomalies that
make the database difficult to use:
COMPANIES(company_name, company_address,
date_founded, owner_name,
owner_title, #shares )
• Anomalies:
– update anomaly occurs if changing the value of an attribute
leads to an inconsistent database state.
– insertion anomaly occurs if we cannot insert a tuple due to some
design flaw.
– deletion anomaly occurs if deleting a tuple results in unexpected
loss of information.
• Normalization is the systematic process for removing all
such anomalies in database design.
Fall 2001 Database Systems 4
Update Anomaly
• If a company has three owners, there are three tuples in
the COMPANIES relation for this company
• If this company moves to a new location, the company’s
address must be updated consistently in all three tuples
– updating the company address in just one or two of the tuples
creates an inconsistent database state
• It would be better if the company name and address
were in a separate relation so that the address of each
company appears in only one tuple
COMPANIES(company_name, company_address,
date_founded, owner_name,
owner_title, #shares )

3. Functional Dependencies
3
Fall 2001 Database Systems 5
Insert Anomaly
• Suppose that three people have just created a new
company:
– the three founders have no titles yet
– stock distributions have yet to be defined
• The new company cannot be added to the COMPANIES
relation because there is not enough information to fill in
all the attributes of a tuple
– at best, null values can be used to complete a tuple
• It would be better if owner and stock information was
stored in a different relation
COMPANIES(company_name, company_address,
date_founded, owner_name,
owner_title, #shares )
Fall 2001 Database Systems 6
Delete Anomaly
• Suppose that an owner of a company retires so is no
longer an owner but retains stock in the company
• If this person’s tuple is deleted from the COMPANIES
relation, then we lose the information about how much
stock the person still owns
• If the stock information was stored in a different relation,
then we can retain this information after the person is
deleted as an owner of the company
COMPANIES(company_name, company_address,
date_founded, owner_name,
owner_title, #shares )

4. Functional Dependencies
4
Fall 2001 Database Systems 7
What to do?
• Take each relation individually and “improve” it in terms
of the desired characteristics
– Normal forms
• Atomic values (1NF)
• Can be defined according to keys and dependencies.
• Functional Dependencies ( 2NF, 3NF, BCNF)
• Multivalued dependencies (4NF)
– Normalization
• Normalization is a process of concept separation which applies a
top-down methodology for producing a schema by subsequent
refinements and decompositions.
• Do not combine unrelated sets of facts in one table; each relation
should contain an independent set of facts.
• Universal relation assumption
• 1NF to 3NF; 1NF to BCNF
Fall 2001 Database Systems 8
Normalization Issues
• How do we decompose a schema into a desirable normal form?
• What criteria should the decomposed schemas follow in order to
preserve the semantics of the original schema?
– Reconstructability: recover the original relation
no spurious joins
– Lossless decomposition: no information loss
– Dependency preservation: the constraints (i.e., dependencies) that hold
on the original relation should be enforceable by means of the
constraints (i.e., dependencies) defined on the decomposed relations.
• What happens to queries?
– Processing time may increase due to joins
– Denormalization

5. Functional Dependencies
5
Fall 2001 Database Systems 9
Keys in the relational model
• Superkey
– A set of one or more attributes, which, taken collectively, allow
us to identify uniquely a tuple in a relation.
– Let R be a relation scheme. A subset K of R is a superkey of R if,
in any legal relation [instance] r of R, for all pairs t1 and t2 of
tuples in r such that t1[K] = t2[K]
t1 = t2.
• Candidate key
– A superkey for which no proper subset is a superkey.
• Primary key
– The candidate key that is chosen by the database designer as
the principle key.
Fall 2001 Database Systems 10
Functional Dependencies
• A functional dependency is a constraint
between two sets of attributes in a relational
database.
• If X and Y are two sets of attributes in the same
relation T, then X → Y means that X functionally
determines Y so that
– the values of the attributes in X uniquely determine
the values of the attributes in Y
– for any two tuples t1 and t2 in T, t1[X] = t2[X] implies
that t1[Y] = t2[Y]
– if two tuples in T agree in their X column(s), then their
Y column(s) should also be the same.

6. Functional Dependencies
6
Fall 2001 Database Systems 11
Functional Dependencies
• Dependencies for
this relation:
– A → B
– A → D
– B,C → E,F
• Do they all hold in
this instance of
the relation R?
¡ ¢ £ ¤ ¥ ¦
§©¨ ¨ ¨ ¨ ¨ ¨
§©¨ ¨ ¨ !
§© ¨ !
§ !
§© ¨ ! ! #
§$ ¨ ¨ % ¨ ¨
• Functional dependencies are specified by the database
programmer based on the intended meaning of the
attributes.
Fall 2001 Database Systems 12
Functional Dependencies
• What are the functional dependencies in:
COMPANIES(company_name, company_address,
date_founded, owner_name,
owner_title, #shares )
company_name → company_address
company_name → date_founded
company_name, owner_id → owner_title
company_name, owner_id → #shares
company_name, owner_title → owner_id
owner_id → owner_name

7. Functional Dependencies
7
Fall 2001 Database Systems 13
Armstrong’s Axioms
• Armstrong’s Axioms: Let X, Y be sets of attributes
from a relation T.
[1] Inclusion rule: If Y⊆ X, then X → Y.
[2] Transitivity rule: If X → Y, and Y → Z, then X → Z.
[3] Augmentation rule: If X → Y, then XZ → YZ.
• Other derived rules:
[1] Union rule: If X → Y and X → Z, then X → YZ
[2] Decomposition rule: If X → YZ, then X → Y and X → Z
[3] Pseudotransitivity: If X → Y and WY → Z, then XW → Z
[4] Accumulation rule: If X → YZ and Z → BW,
then X → YZB
Fall 2001 Database Systems 14
Closure
• Let F be a set of functional dependencies.
• We say F implies a functional dependency g if g
can be derived from the FDs in F using the
axioms.
• The closure of F, written as F+, is the set of all
FDs that are implied by F.
• Example: Given FDs { A → BC, C → D, AD → B },
what is the closure?
The closure is:
{ A → BC, C → D, AD → B, A → D }

8. Functional Dependencies
8
Fall 2001 Database Systems 15
Cover and Minimal Cover
• A set F of functional dependencies is said to cover
another set G of function dependencies iff G ⊆ F+.
– in other words, all dependencies in G can be derived from the
dependencies in F.
– if both F covers G, and G covers F then F and G are said to be
equivalent, written as F ≡ G.
– Given F = { A → BC, C → D, AD → B }
G = {A → B, C → D }
Does F cover G? Does G cover F?
• A minimal cover for a set F of functional dependencies is
a minimal set M that covers F.
Fall 2001 Database Systems 16
Closure of a set of attributes
• Given a set of F of functional dependencies, the
closure of a set of attributes X, denoted by X+ is
the largest set of attributes Y such that X → Y.
Algorithm Closure(X,F)
X[0] = X; I = 0;
repeat
I = I + 1;
X[I] = X[I-1];
FOR ALL Z → W in F
IF Z ⊆ X[I] THEN X[I] = X[I] ∪ W
END FOR
until X[I] = X[I-1];
RETURN X+ = X[I]

9. Functional Dependencies
9
Fall 2001 Database Systems 17
Minimal Cover Algorithm
• Given a set F of functional dependencies,
find a minimal cover M for F.
– Step 1. Decompose all FDs of the form X →
a1…an to a set of functional dependencies with
a single attribute on the right side, i.e. X → a1, …
, X → an
– Step 2. Remove all inessential FDs from F
for all X → A in F
find H = F - { X → A }
If A ⊆ X+ in H, then remove X → A
end for
Fall 2001 Database Systems 18
– Step 3. For all FDs, try to remove attributes from the
left hand side as long as the result does not change
F+.
for all X → A in F
let Y = X - {b} for some attribute b
let G = (F - {X → A}) ∪ {Y → A}
if Y+ under G is equal to Y+ under F then
set F = G (I.e. remove b from the given
FD)
end for
– Step 4. Gather all FDs with the same left hand side
using the union rule

10. Functional Dependencies
10
Fall 2001 Database Systems 19
Minimal Cover Exercise
• Compute the minimal cover of the following set
of functional dependencies:
{ ABC → DE, BD → DE, E → CF, EG → F }
The minimal cover is:
{ ABC → D, BD → E, E → CF }
Fall 2001 Database Systems 20
Lossless Decomposition
• Given a table T, a lossless decomposition of T
inko k tables is a set of tables {T1,T2,…,Tk} such
that
– head(T) = head(T1) ∪ head(T2) ∪ … ∪ head(Tk)
i.e., the decomposed tables contain all attributes from the
original table
– each Ti contains the table T projected onto columns
head(Ti)
– lossless condition: T = T1
¡£¢ T2
¡£¢ …
¡£¢ Tk
i.e., the decomposed tables will contain the same
information as T, no more and no less

11. Functional Dependencies
11
Fall 2001 Database Systems 21
¡ ¢ £ ¤
¥§¦ ¨©¦ ¦ ¦
¥§¦ ¨©¦ ¦
¥§ ¨©¦ ©
¥ ¨©
¥ ¨©¦ ¦ ¦
! # $
%' (
%') (
%§0 ()
%21 (
354 6 7 8
9©@ A@ B@
9©@ AC B@
9©@ AC B©D
9©C AD BE
F5GIH5PRQTS U V W X
Y` a§` b` c©`
Y` a§` b2d c©`
Y` a§` b2d c'e
Yd a§` b` c©`
Yd a§` b2d c©`
Yd a§` b2d c'e
Ye ad b2e cf
Ygf a§` b` c©`
Ygf a§` b2d c©`
Ygf a§` b2d c'e
{R1, R2} is not a
lossless decompostion
of relation R.
The first and second
parts of the definition
are satisfied, but not
the third part.
Fall 2001 Database Systems 22
Lossless Decompositions
• Given a table T and a set of attributes X ⊆ head(T) the
following statements are equivalent:
– X is a superkey of T
– X → head(T)
– X functionally determines all attributes in T
– X+ = head(T)
• Given a table T with a set F of functional dependencies
valid on T, a decomposition of T into tables {T1,T2} is a
lossless decomposition if one of the following
decompositions is implied by F:
(1) head(T1) ∩ head(T2) → head(T1)
(2) head(T1) ∩ head(T2) → head(T2)
i.e., the attributes in common between the two tables
determine all attributes in one of the new tables

12. Functional Dependencies
12
Fall 2001 Database Systems 23
Lossless Decompositions
• Let head(T) = {A,B,C,D,E,F} with functional
dependencies:
– AB → CD
– AE → D
– C → F
• Which of the following are lossless decompositions?
head(T1) = {A, B, C} head(T2) = {C, D, E, F}
head(T1) = {A, B, C, F} head(T2) = {A, B, D, E}
{A, B, C} ∩ {C, D, E, F} = {C}
But, {C} → {A, B, C} and {C} → {C, D, E, F}
{A, B, C, F} ∩ {A, B, D, E} = {A, B}
{A, B} → {A, B, C} = head(T1), so this is lossless
Fall 2001 Database Systems 24
Preserving Functional Dependencies
• Given a table T and a set of functional
dependencies F, let {T1,T2,…,Tk} be a
decomposition of T
– A functional dependency X → Y in F is said to be
preserved in this decomposition if there exists a table Ti
such that X ∪ Y ⊆ head(Ti).
– In this case, we say that X → Y lies in Ti.
• A decomposition is functional dependency
preserving if all dependencies in (the minimal
cover of) F are preserved.

13. Functional Dependencies
13
Fall 2001 Database Systems 25
Preserving Functional Dependencies
• Given {AB → CD, AE → D, C → F}, which dependencies
are preserved by the following decompositions?
head(T1) = {A, B, C} head(T2) = {C, D, E, F}
head(T1) = {A, B, C, F} head(T2) = {A, B, D, E}
AB → C C → F
Not functional dependency preserving
AB → C AB → D
C → F AE → D
Functional dependency preserving
Fall 2001 Database Systems 26
Boyce-Codd Normal Form
• A table T is said to be in Boyce-Codd Normal Form
(BCNF) with respect to a given set of functional
dependencies F if for all functional dependencies of the
form X → A implied by F the following is true:
If A is a single attribute that is not in X then X is a superkey.
Alternately,
If A is a single attribute that is not in X then X contains all
the attributes in a key.
• Given {AB → C, AB → D, AE → D, C → F} with Key:
{A,B,E}
– not in BCNF since C is a single attribute not in AB, but AB is not
a superkey.

14. Functional Dependencies
14
Fall 2001 Database Systems 27
Boyce-Codd Normal Form
Given head(T)={A,B,C,D,E,F} with functional
dependencies
{AC → D, AC → E, AF → B, AD → F, BC → A, ABC →
F } and keys: {A, C}, {B, C}, is this relation T in
BCNF?
No. It is sufficient to find one violation!
– AF → B violates BCNF since B is not in AF
and AF is not a superkey.
– AD → F violates BCNF since F is not in AD
and AD is not a superkey.
Note: ABC → F does not violate BCNF since
ABC is a superkey.
Fall 2001 Database Systems 28
Normalization
• Given a table T that is not in BCNF, we want to find a
lossless and dependency preserving decomposition for T
such that all sub-tables are in BCNF
Company( company_name, company_address,
date_founded, owner_id, owner_name,
owner_title, #shares )
Functional dependencies
company_name → company_address, date_founded
company_name, owner_id → owner_title, #shares
company_name, owner_title → owner_id
owner_id → owner_name
Keys: {company_name, owner_id}
{company_name, owner_title}
Is it in BCNF?

15. Functional Dependencies
15
Fall 2001 Database Systems 29
Normalization
Company1(company_name, company_address,
date_founded, owner_id, owner_title, #shares)
company_name → company_address, date_founded
company_name, owner_id → owner_title, #shares
company_name, owner_title → owner_id
Company2(owner_id, owner_name)
owner_id → owner_name
Further decompose Company1:
Company11(company_name, company_address, date_founded)
Company12(company_name, owner_id, owner_title, #shares)
Are all the resulting relations in BCNF?
Fall 2001 Database Systems 30
BCNF
• It is not always possible to find a lossless and
dependency preserving decomposition of a relation that
is in BCNF.
• Given: Address(Street, City, State, Zip)
Street, City, State → Zip
Zip → City, State
Keys: {Street, City, State} {Street, Zip}
It is not in BCNF since Zip → City, but {Zip} is not a
superkey.
But, we cannot decompose further, since if we have
Address1(Street, City, State)
Address2(City, Zip)
we loose the functional dependency Street, City, State
→ Zip
• It is not always desirable to normalize relations too far!

16. Functional Dependencies
16
Fall 2001 Database Systems 31
Third Normal Form
• A table T is said to be in third normal form (3NF) with
respect to a given set of functional dependencies F if for
all functional dependencies of the form X → A implied by
F, if A is a single attribute that is not in X, then one of the
following holds:
– X is a superkey for T
– the attribute A is in one of the keys for T
• If a table is BCNF, then it is in third normal form. But,
there are relations that are in 3NF that are not in BCNF.
– Example: The Address relation is 3NF, but not BCNF.
Address(Street, City, State, Zip)
Street, City, State → Zip
Zip → City, State
Fall 2001 Database Systems 32
Algorithm for 3NF Decomposition
Given a table T and a set of functional dependencies F
replace F with minimal cover of F
S = { }
for all X → Y in F
if no table Z in S contains all attributes in X ∪ Y then
S = S ∪ head(X ∪ Y) /* create a table containing
attributes in X ∪ Y */
end-for
for all candidate keys K for T
if no table Z in S contains all attributes in K then
S = S ∪ head(K) /* create a new table with
attributes in K*/
end for

17. Functional Dependencies
17
Fall 2001 Database Systems 33
Exercise
• Given relation T, with head(T)={A,B,C,D,E,F} and
functional dependencies {AE → DF, BE → F, B → A, AD
→ C}, compute a decomposition that is in 3NF.
A 3NF decomposition is:
head(T1) = {A, E, D}
head(T2) = {A, E, F}
head(T3) = {B, A}
head(T4) = {A, D, C}
head(T5) = {B, E}