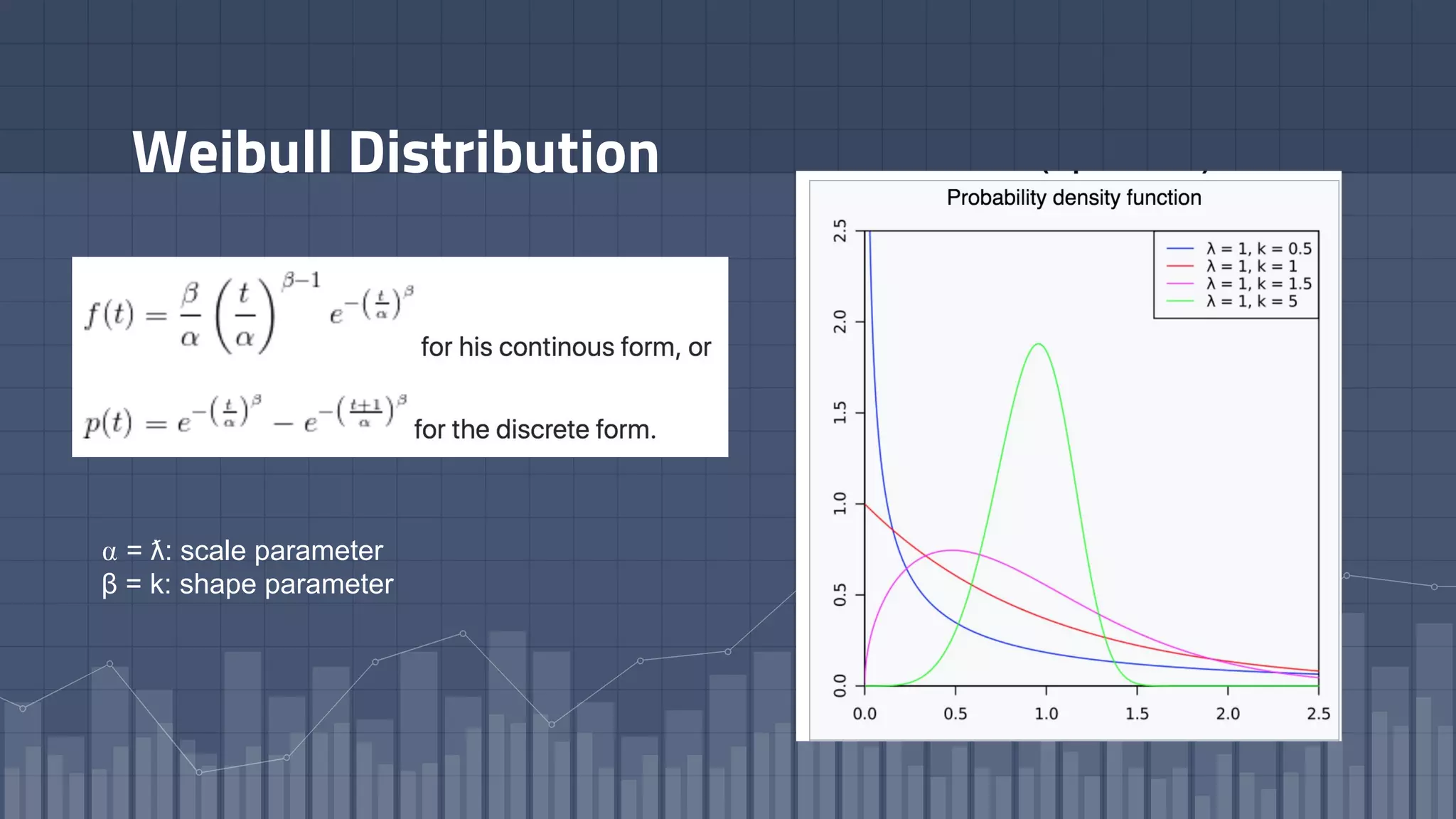
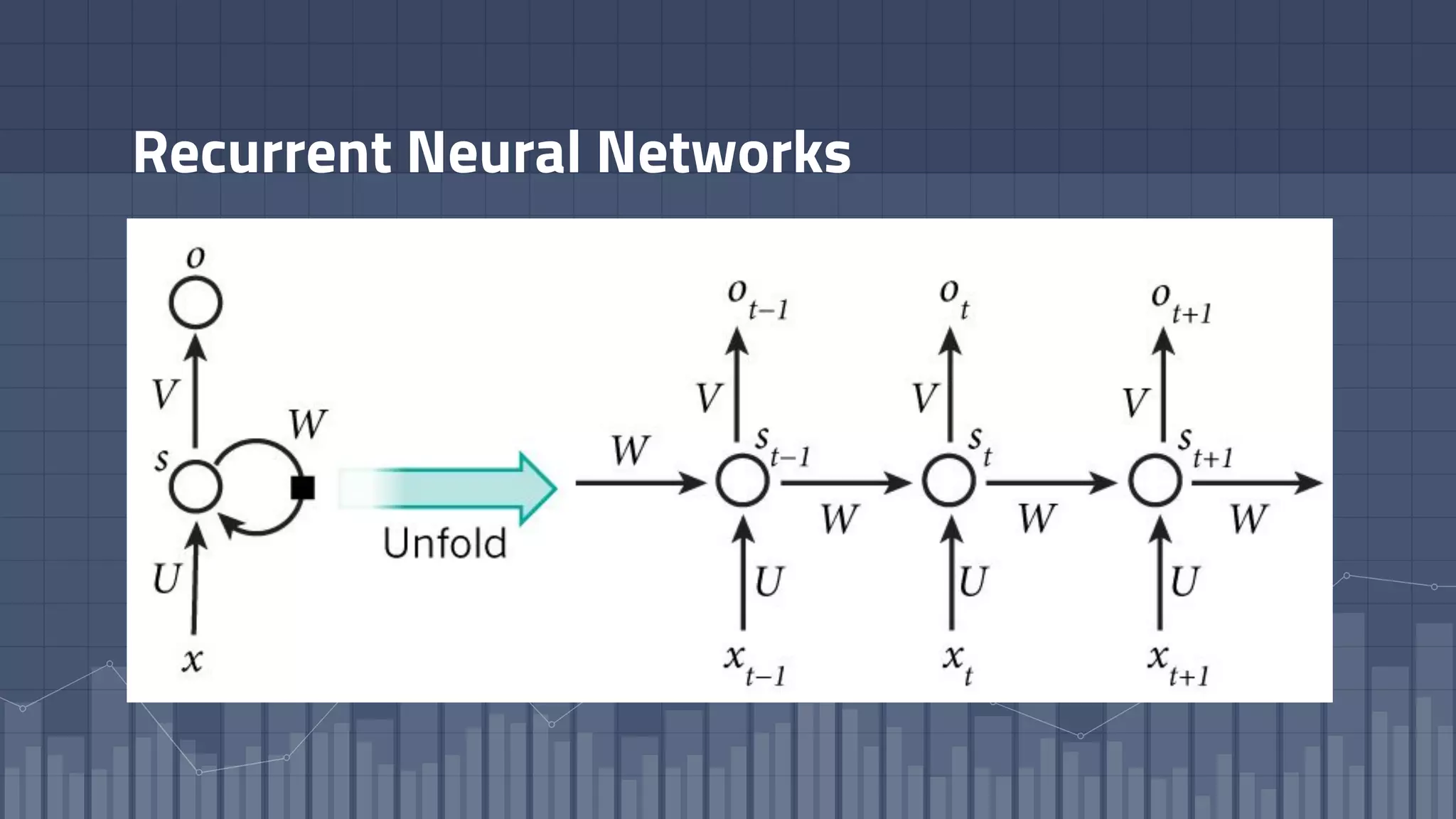
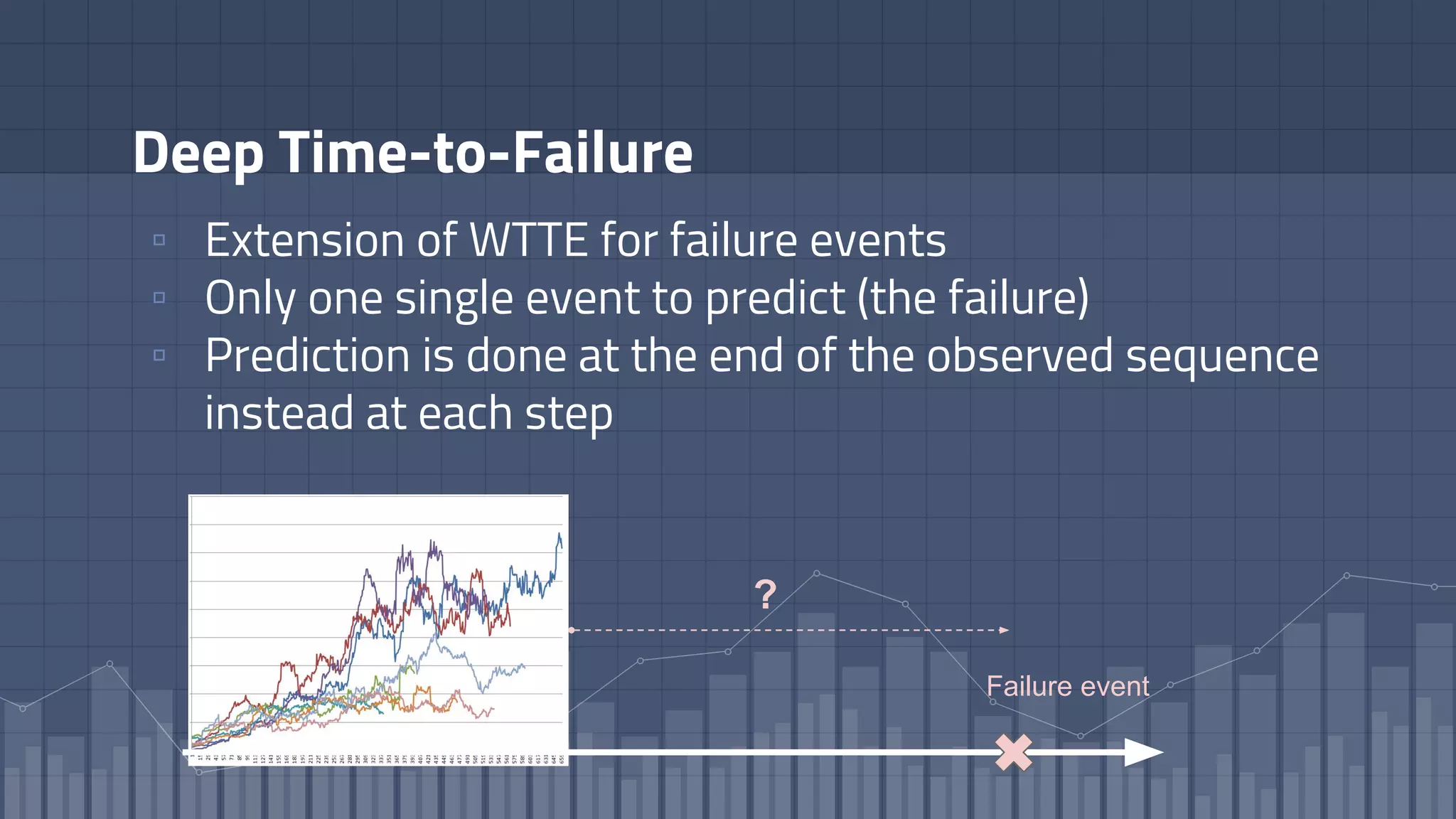
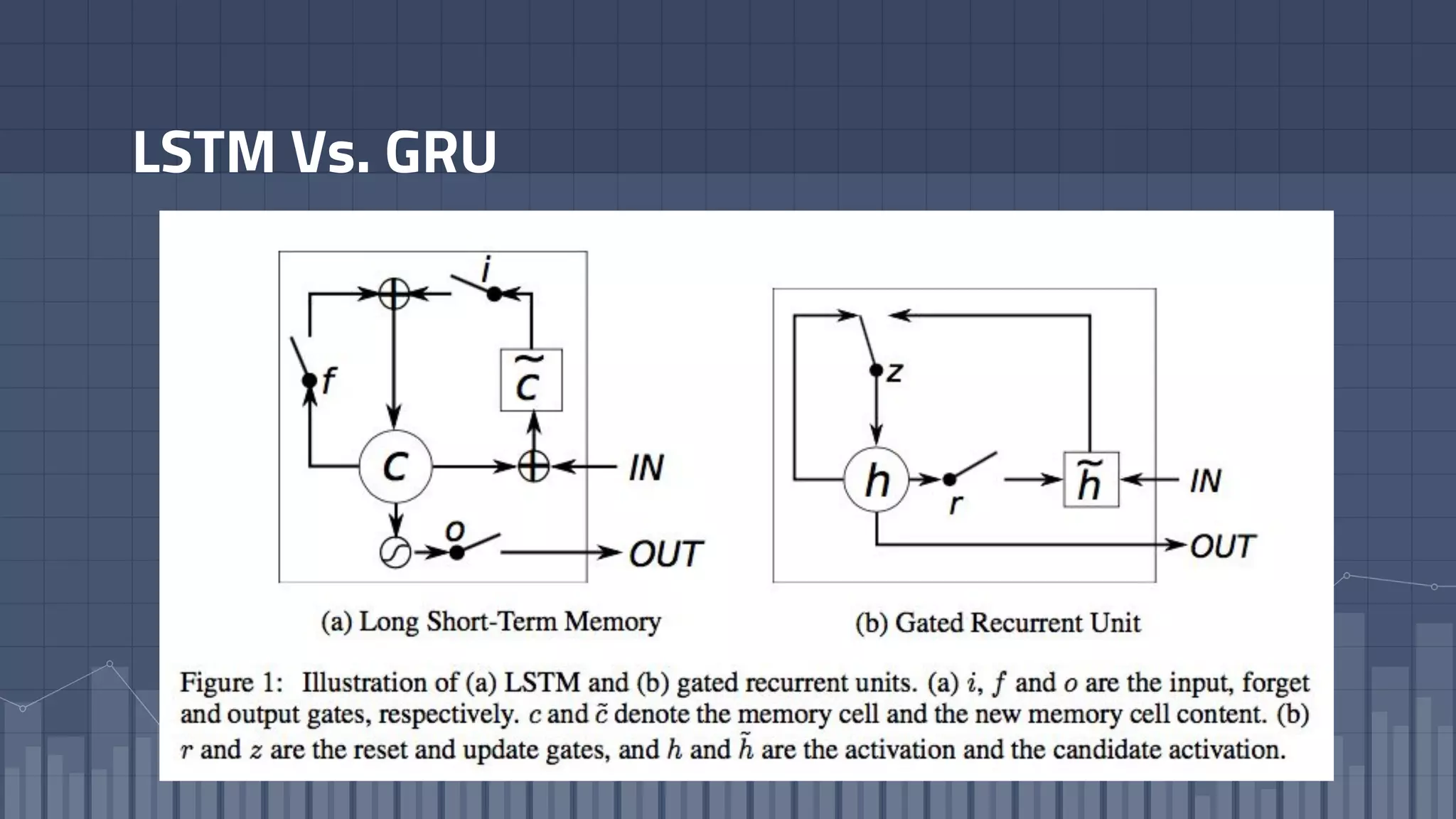
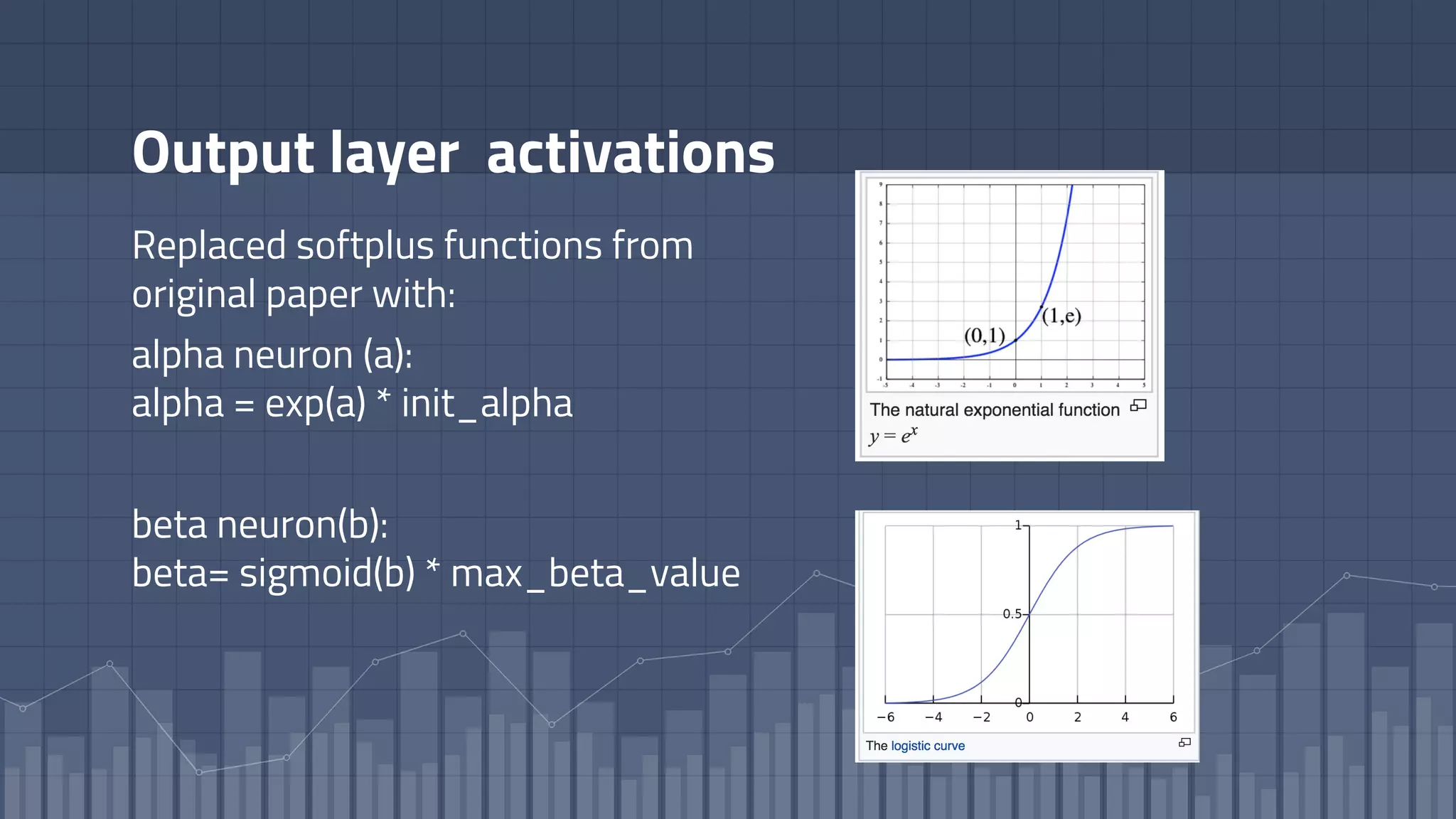
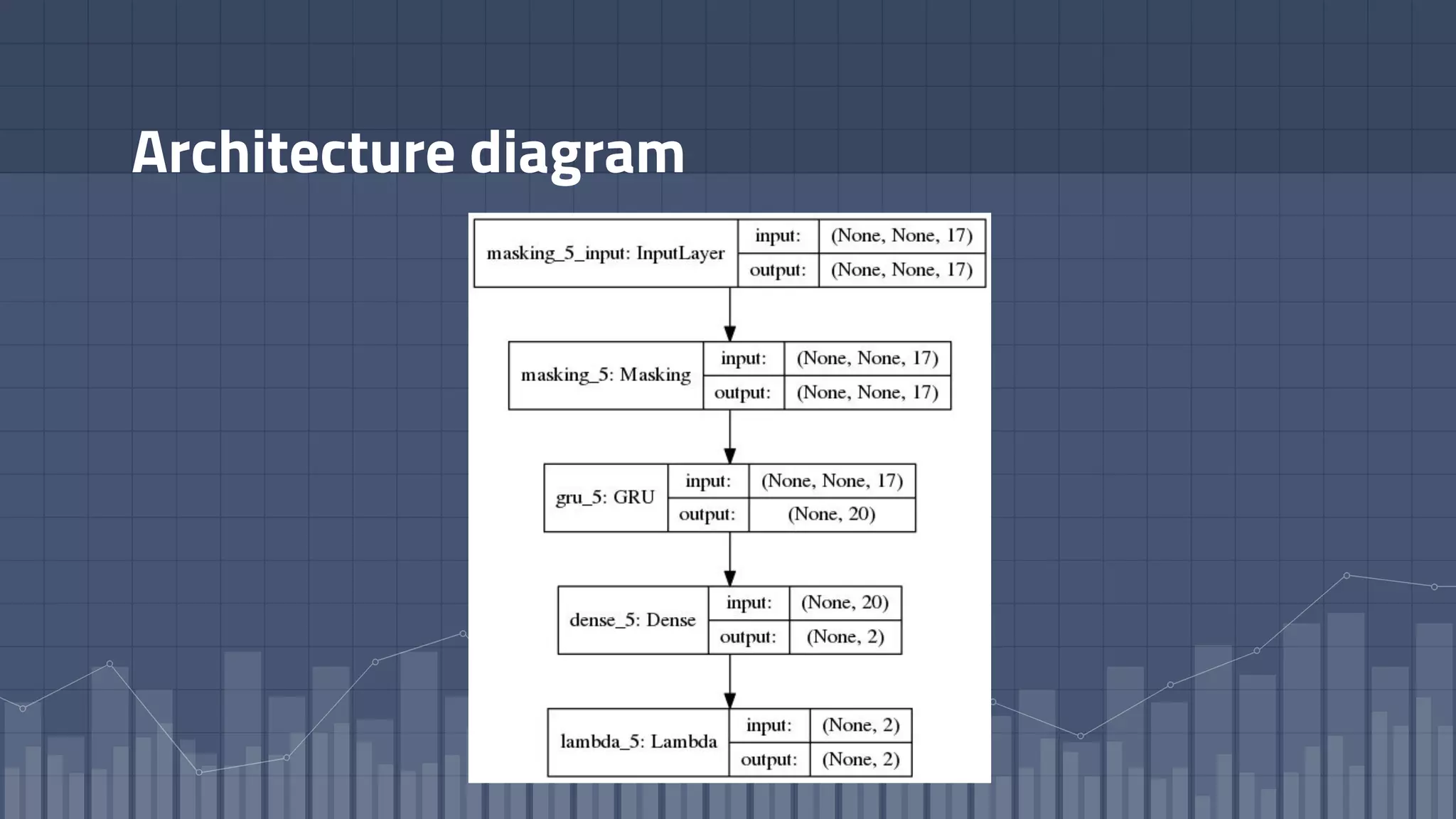
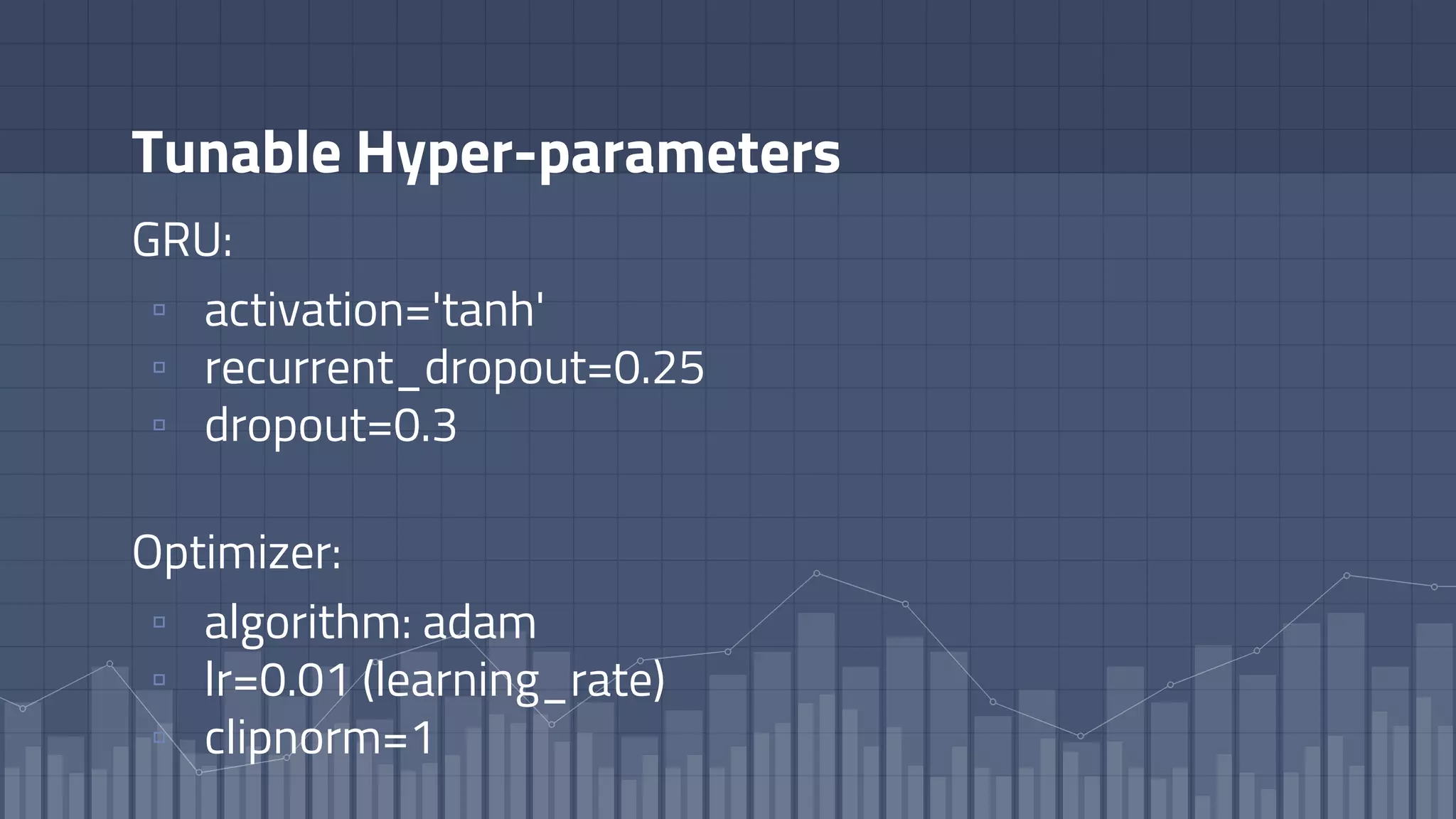
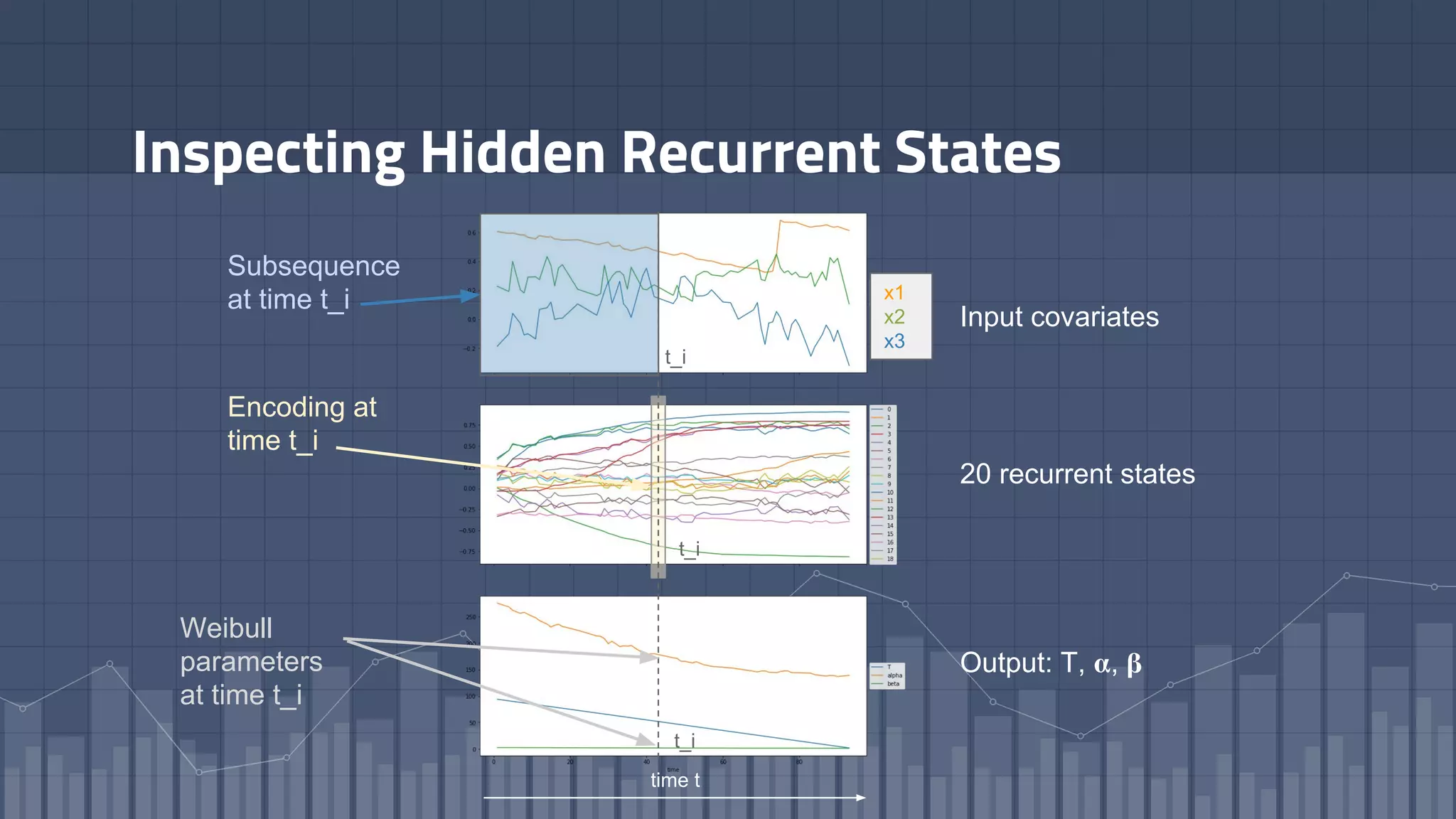
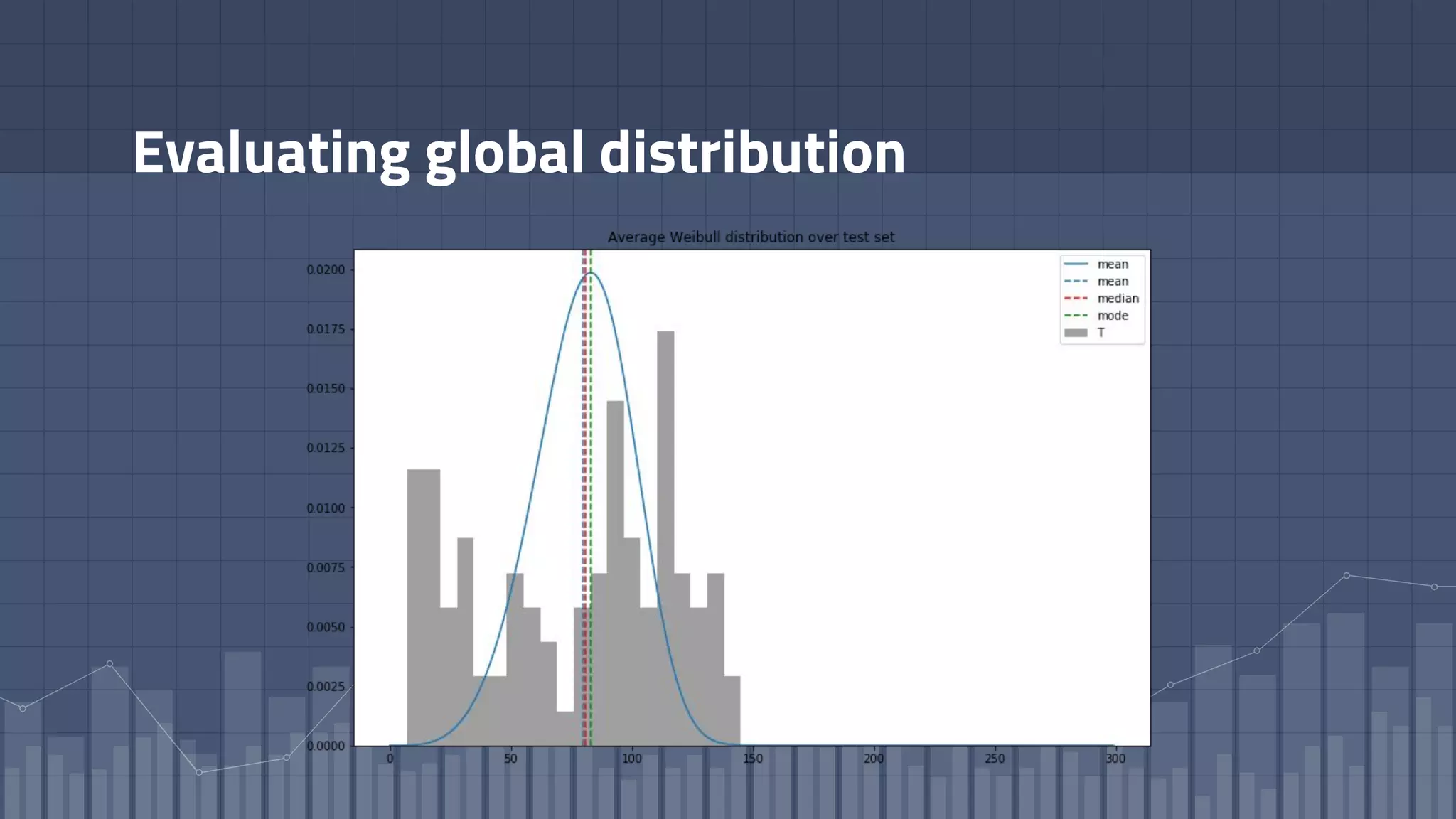
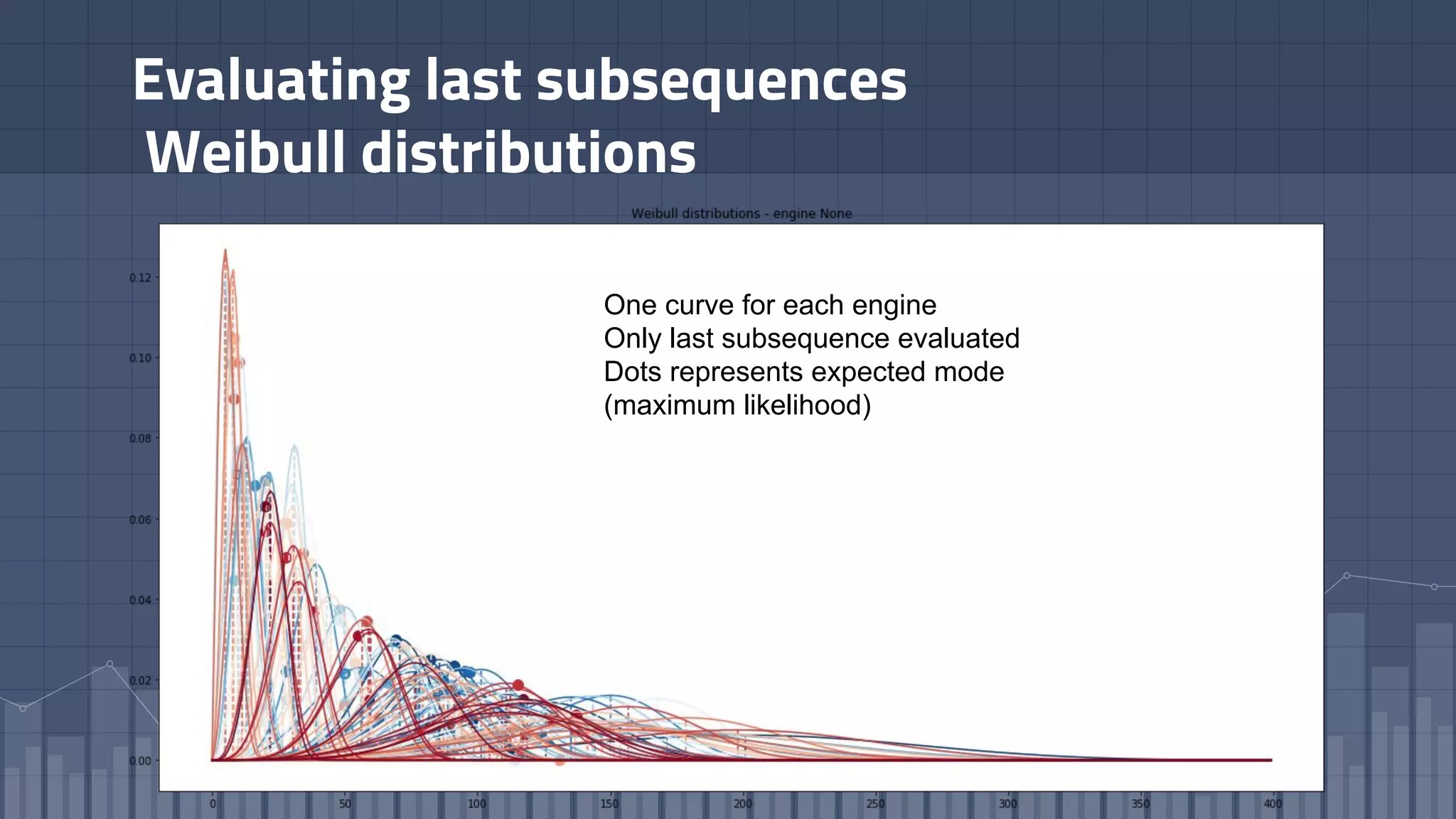
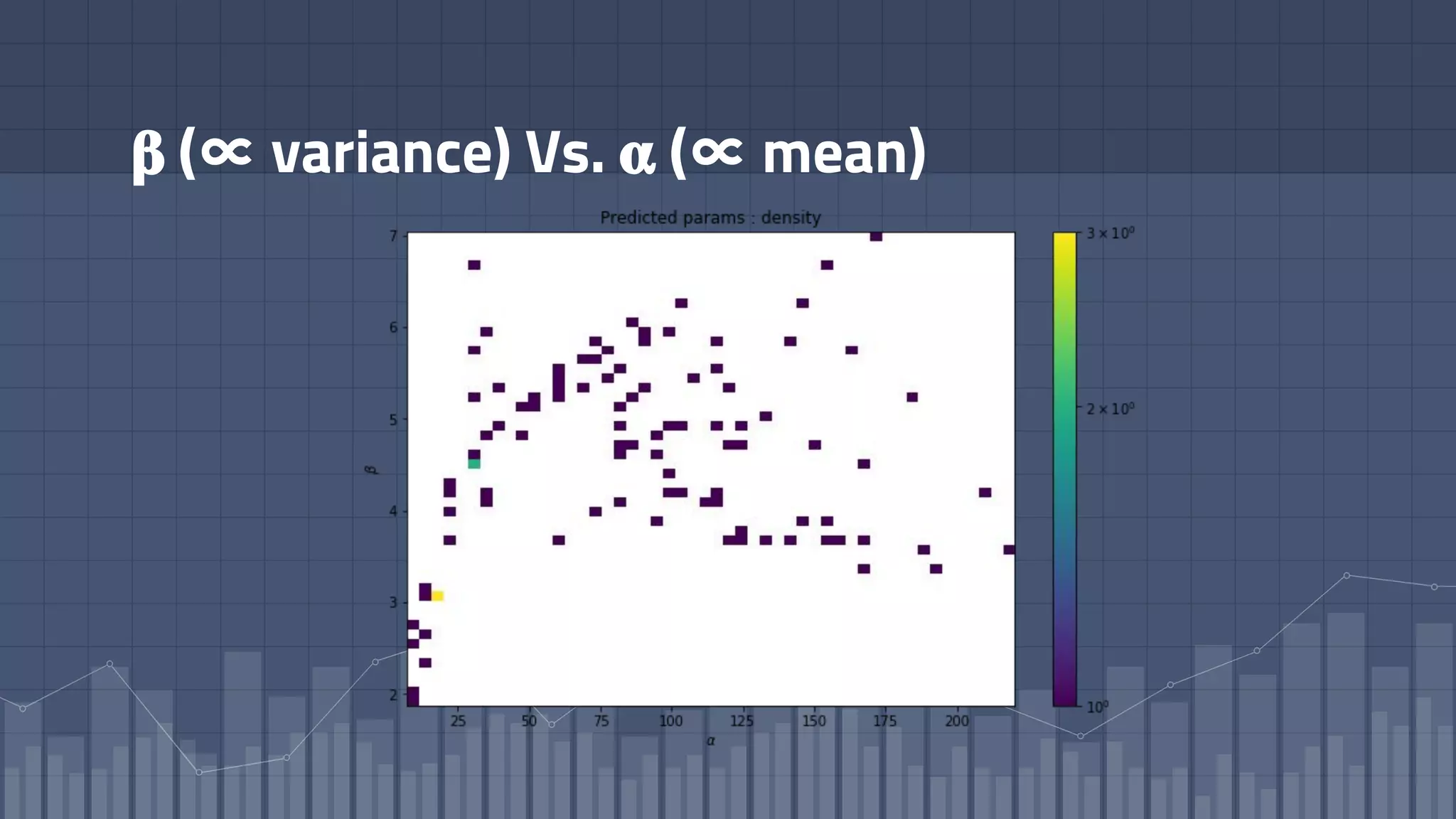
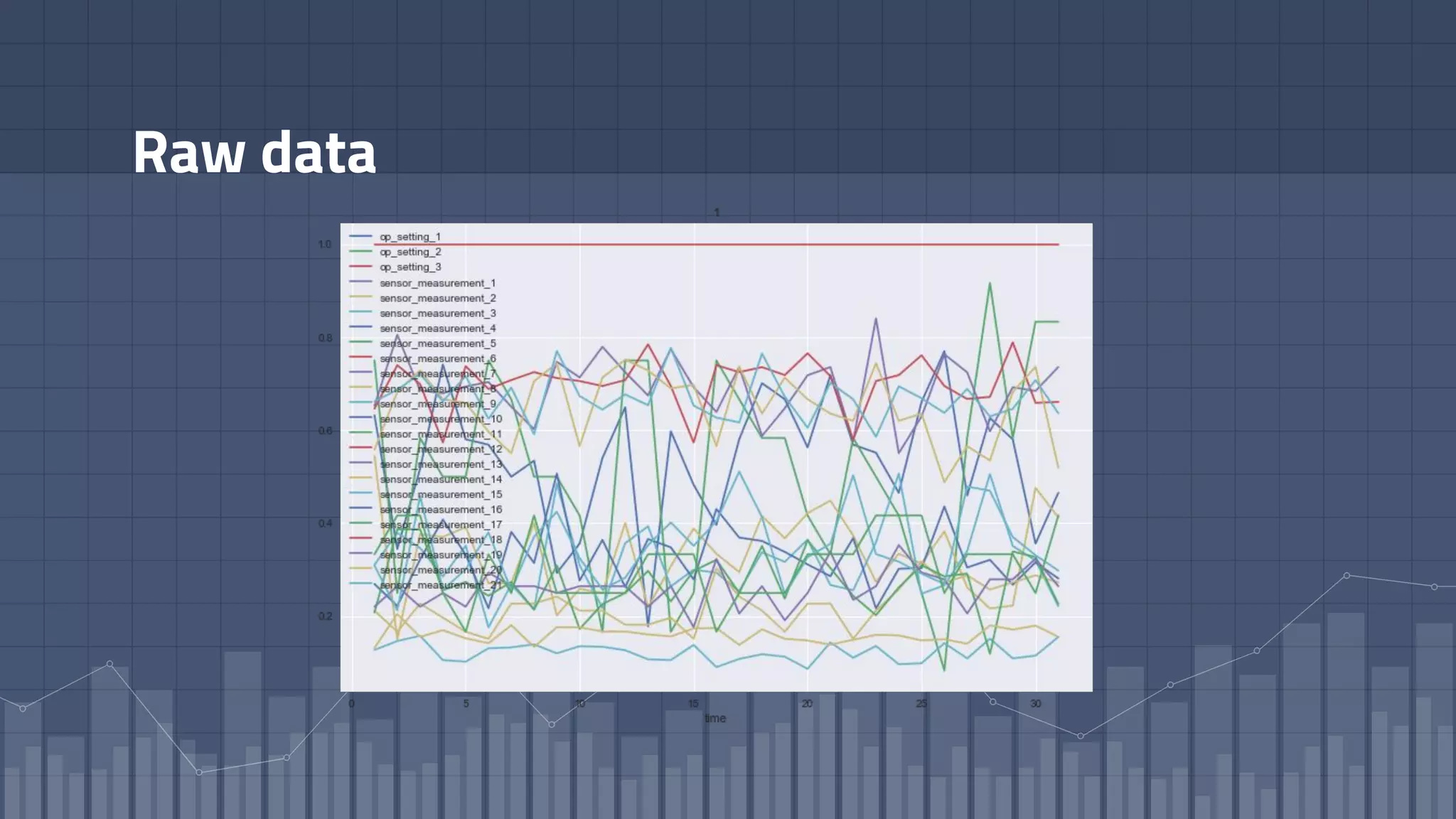
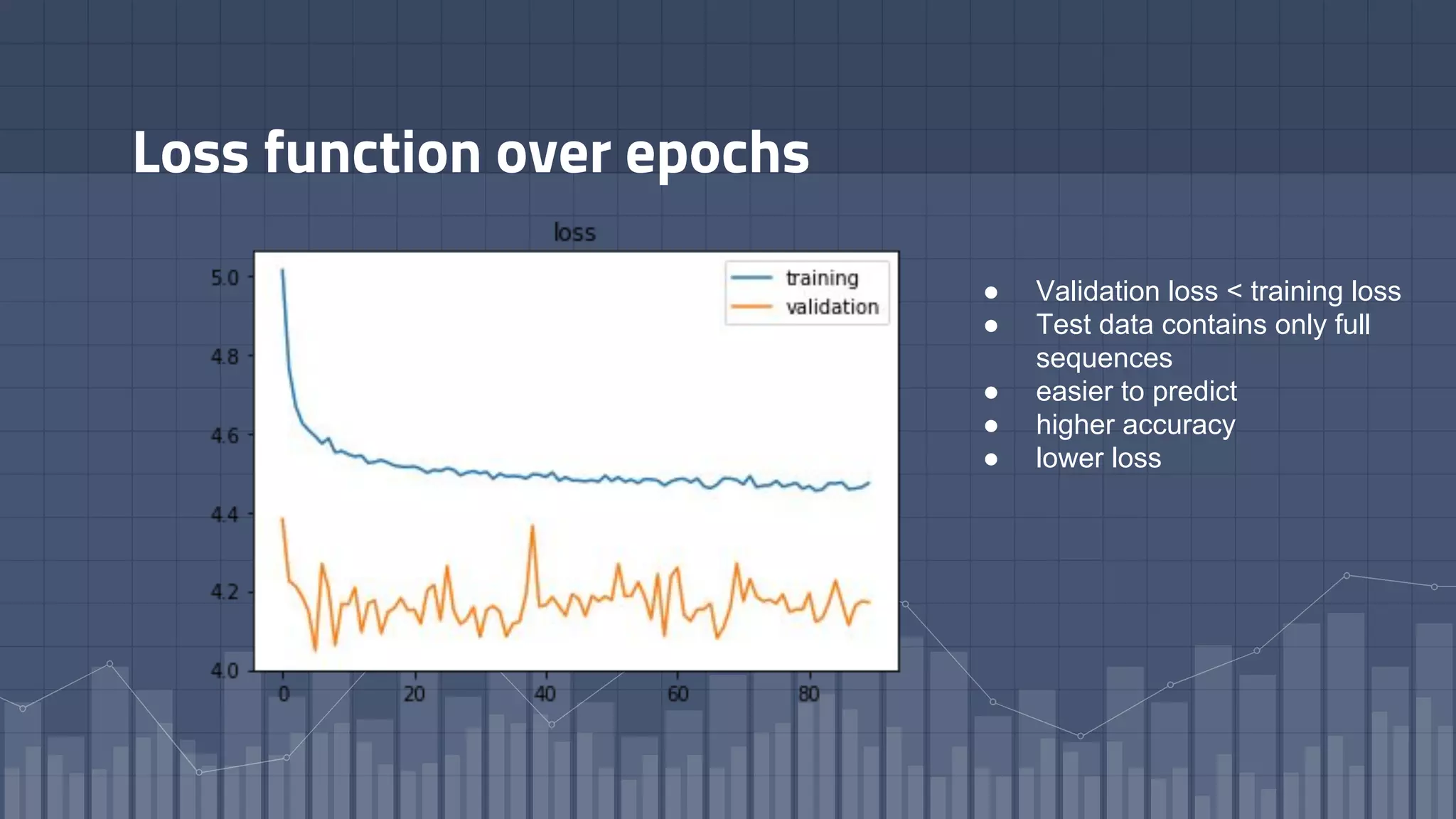
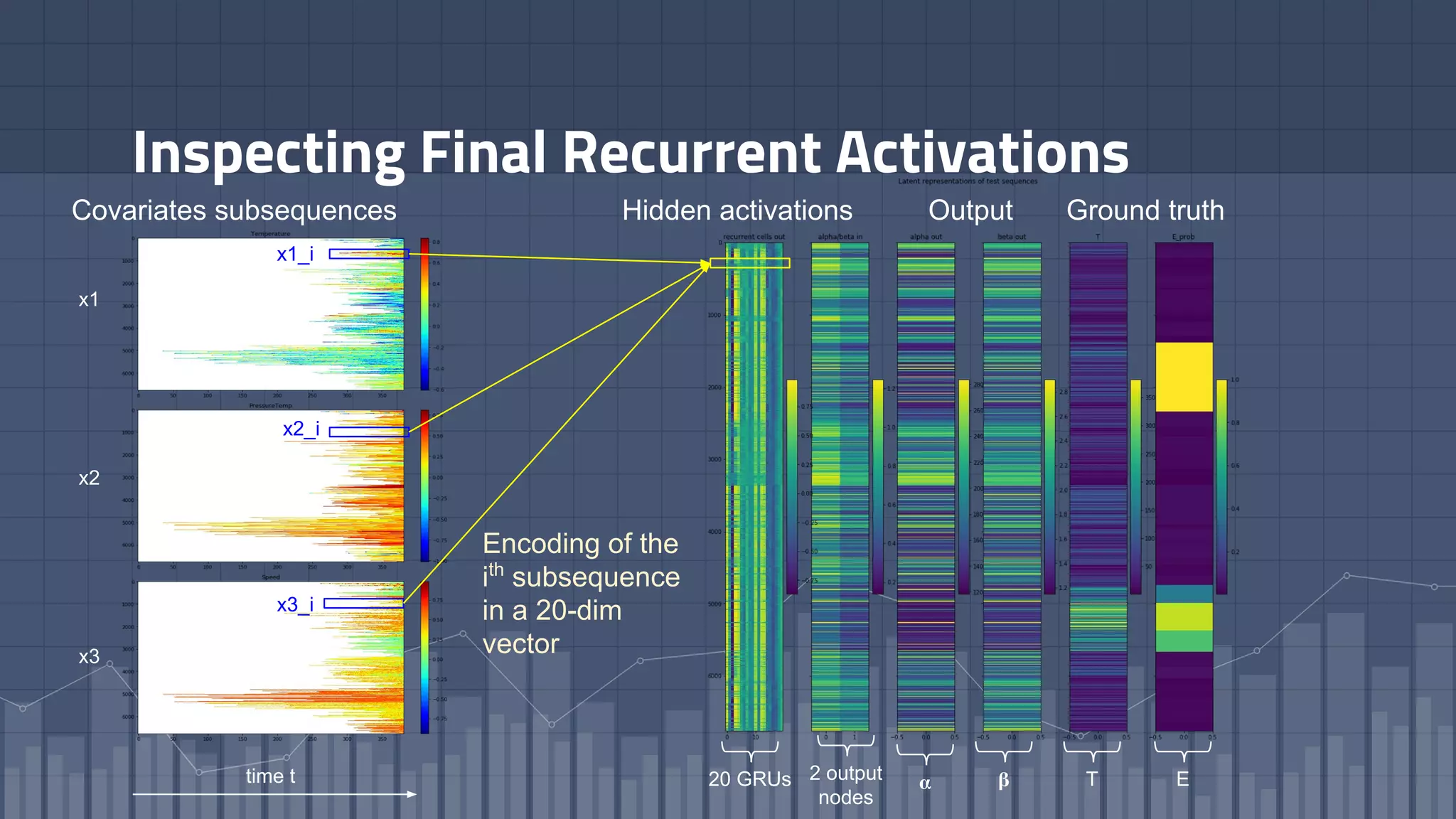
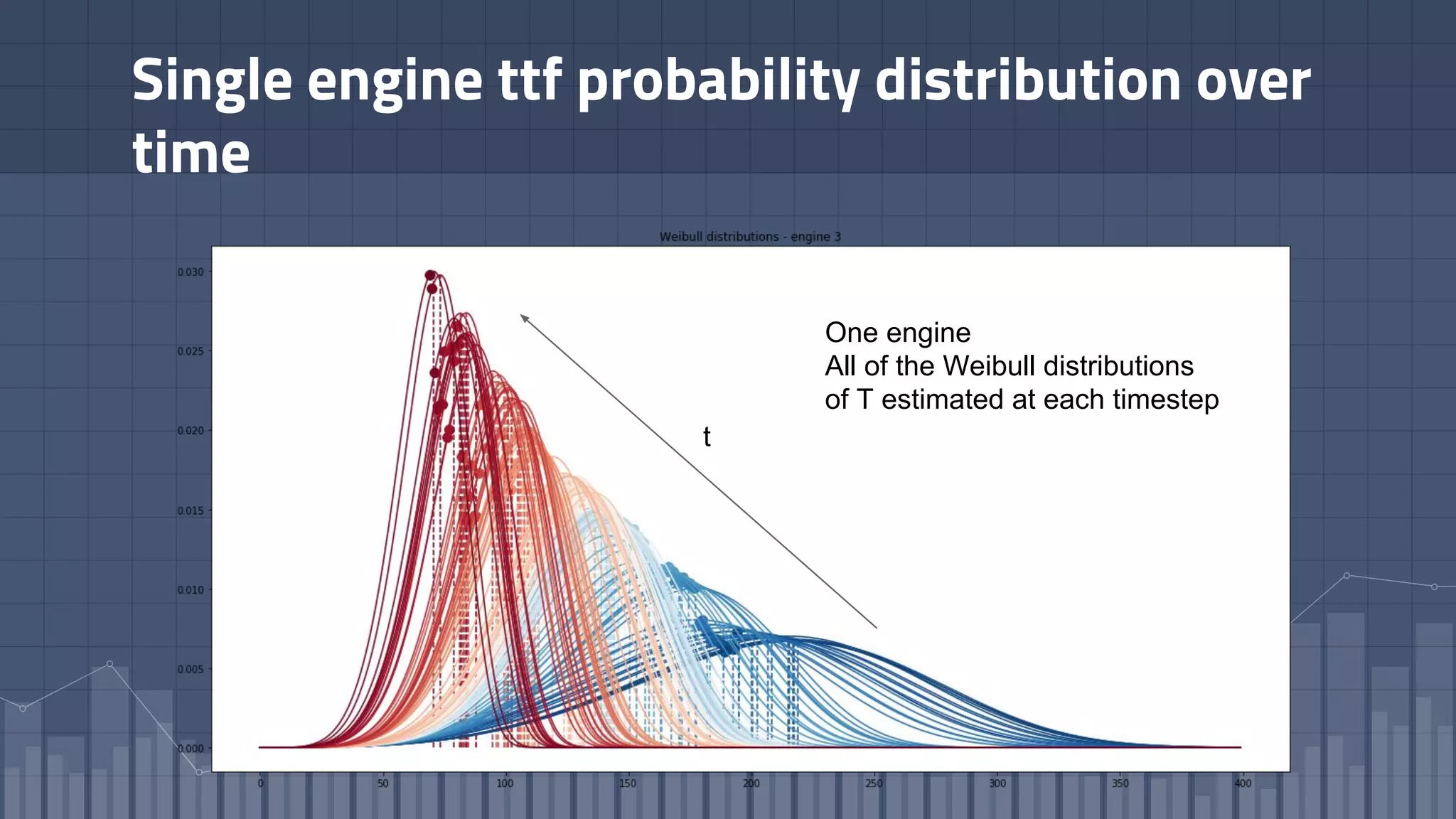
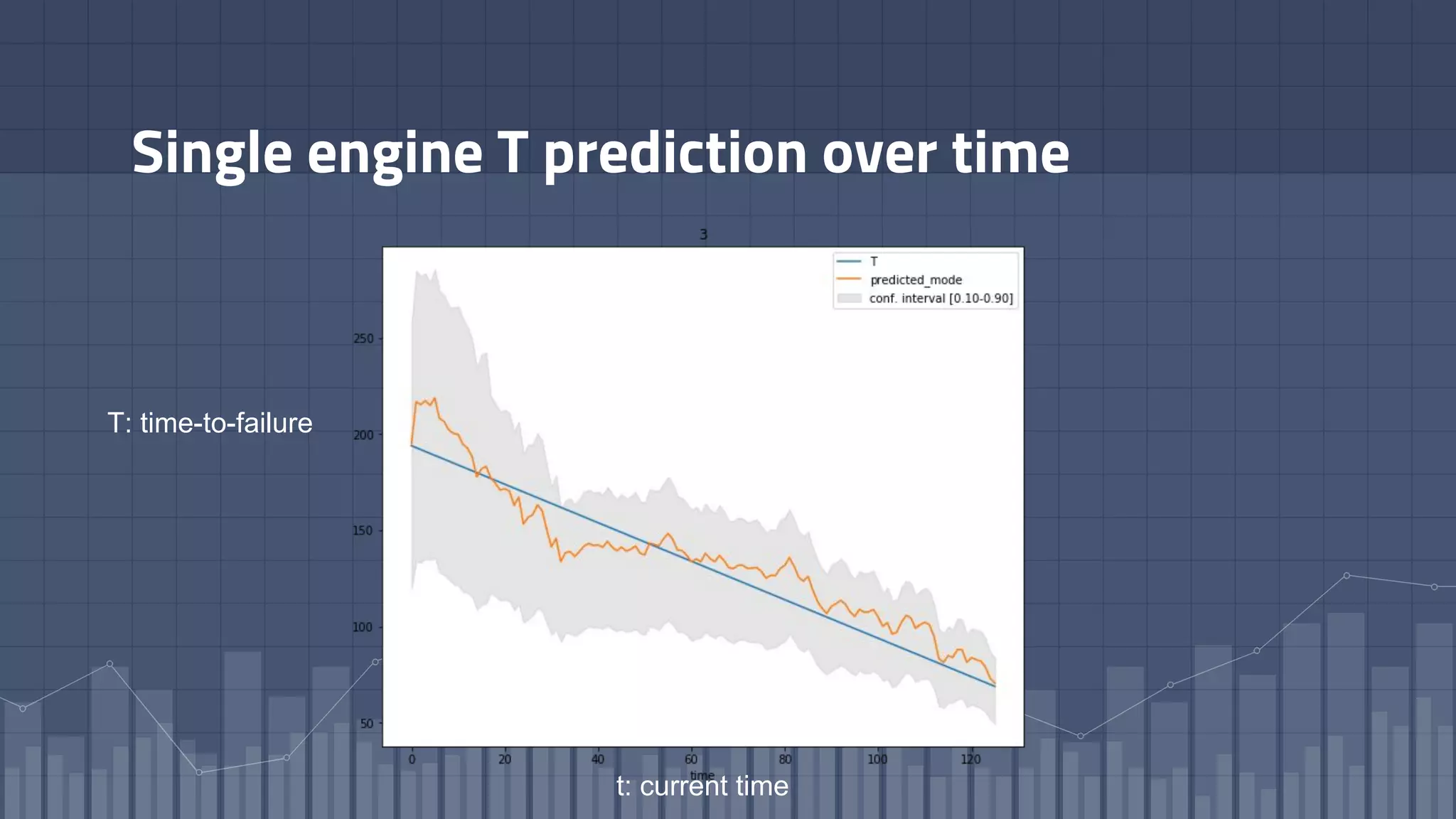
1. The document discusses using deep learning models like recurrent neural networks to predict time-to-failure events from time series data. It specifically focuses on a technique called Deep Time-to-Failure which extends a Weibull Time-to-Event Recurrent Neural Network to predict a single failure event. 2. As a case study, the technique is applied to predict failure times of NASA jet engines using sensor data as inputs. The model is trained on historical sequences of data to learn the distribution of time-to-failure and can provide probabilistic predictions and confidence intervals. 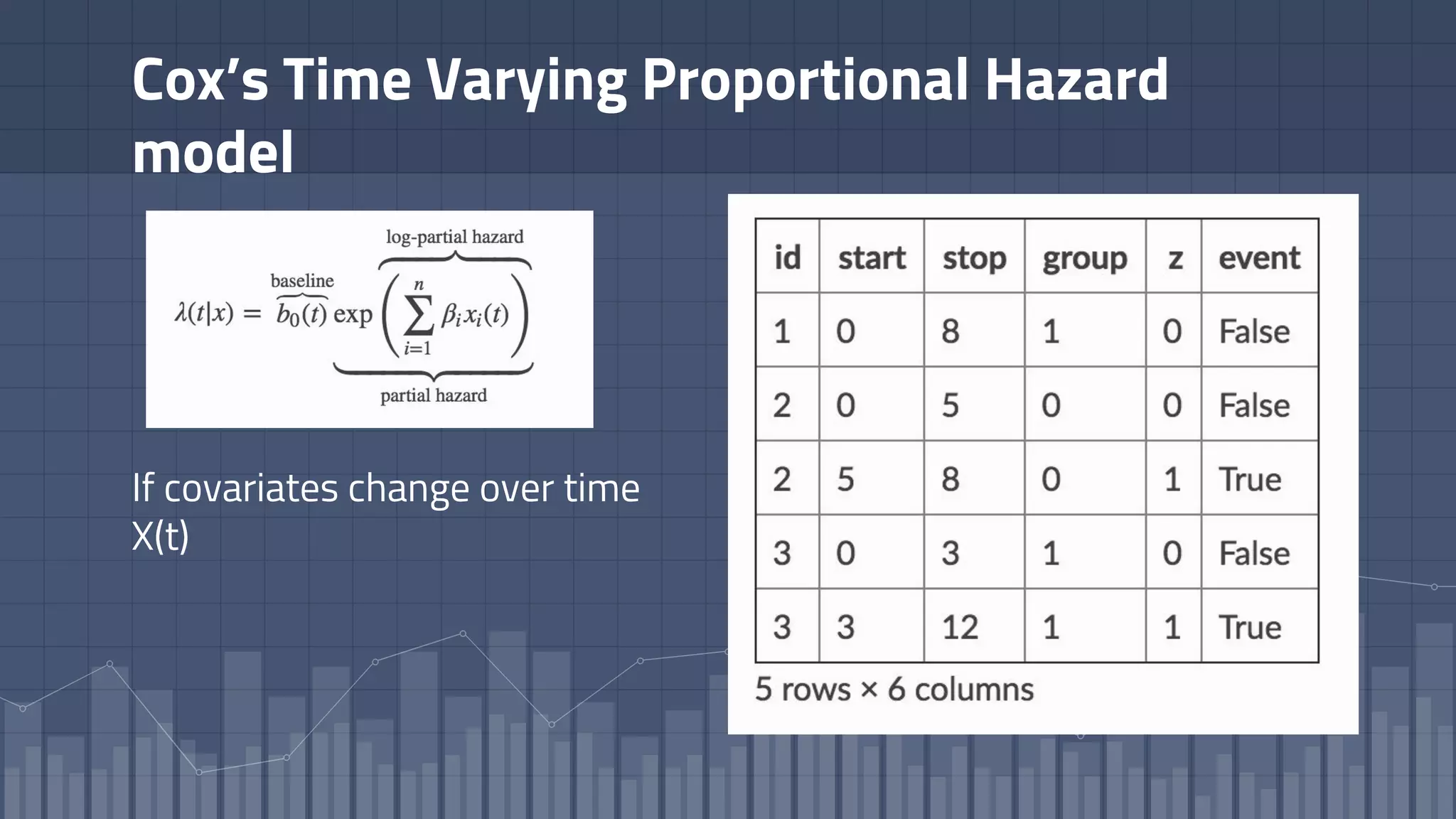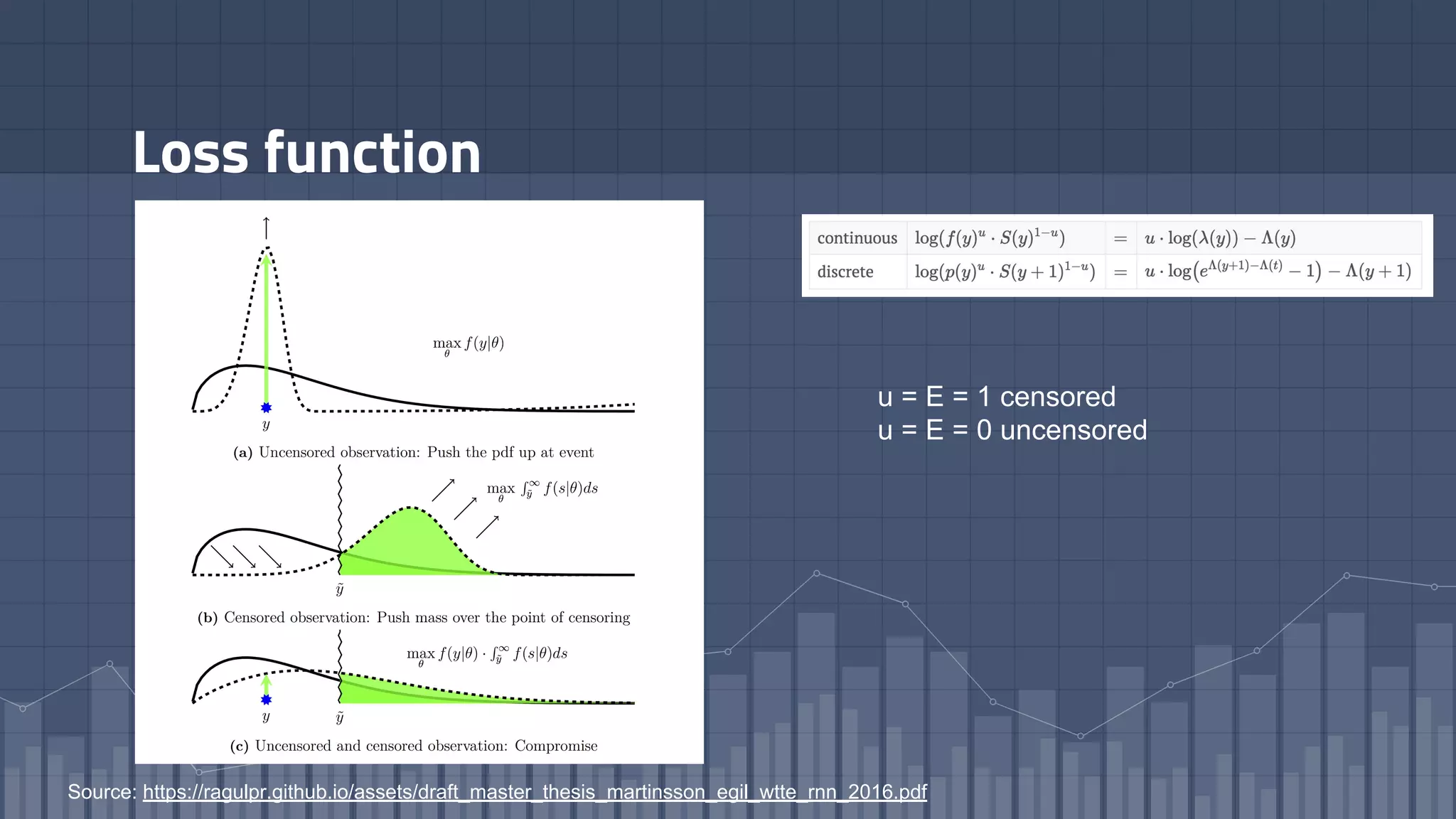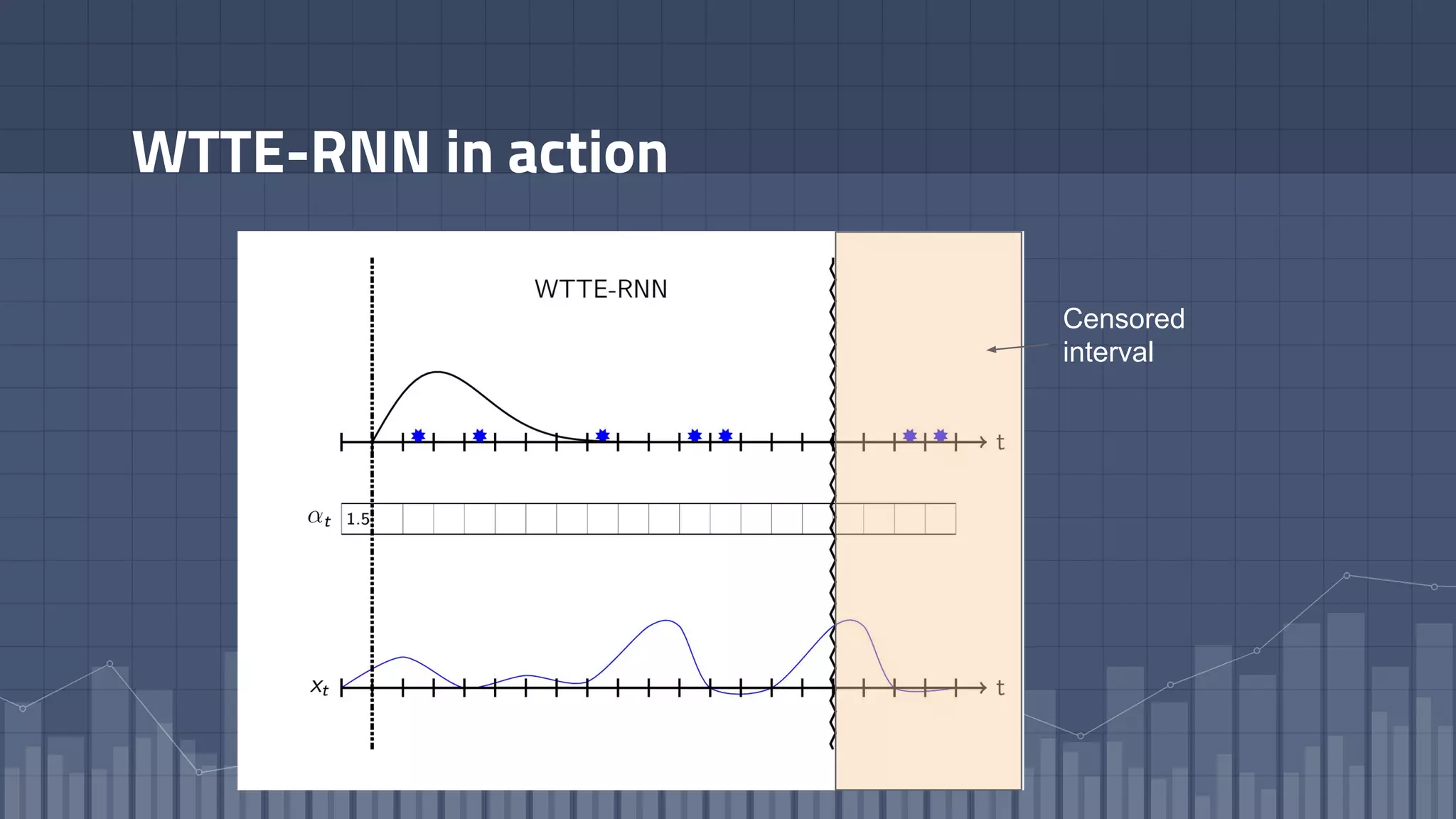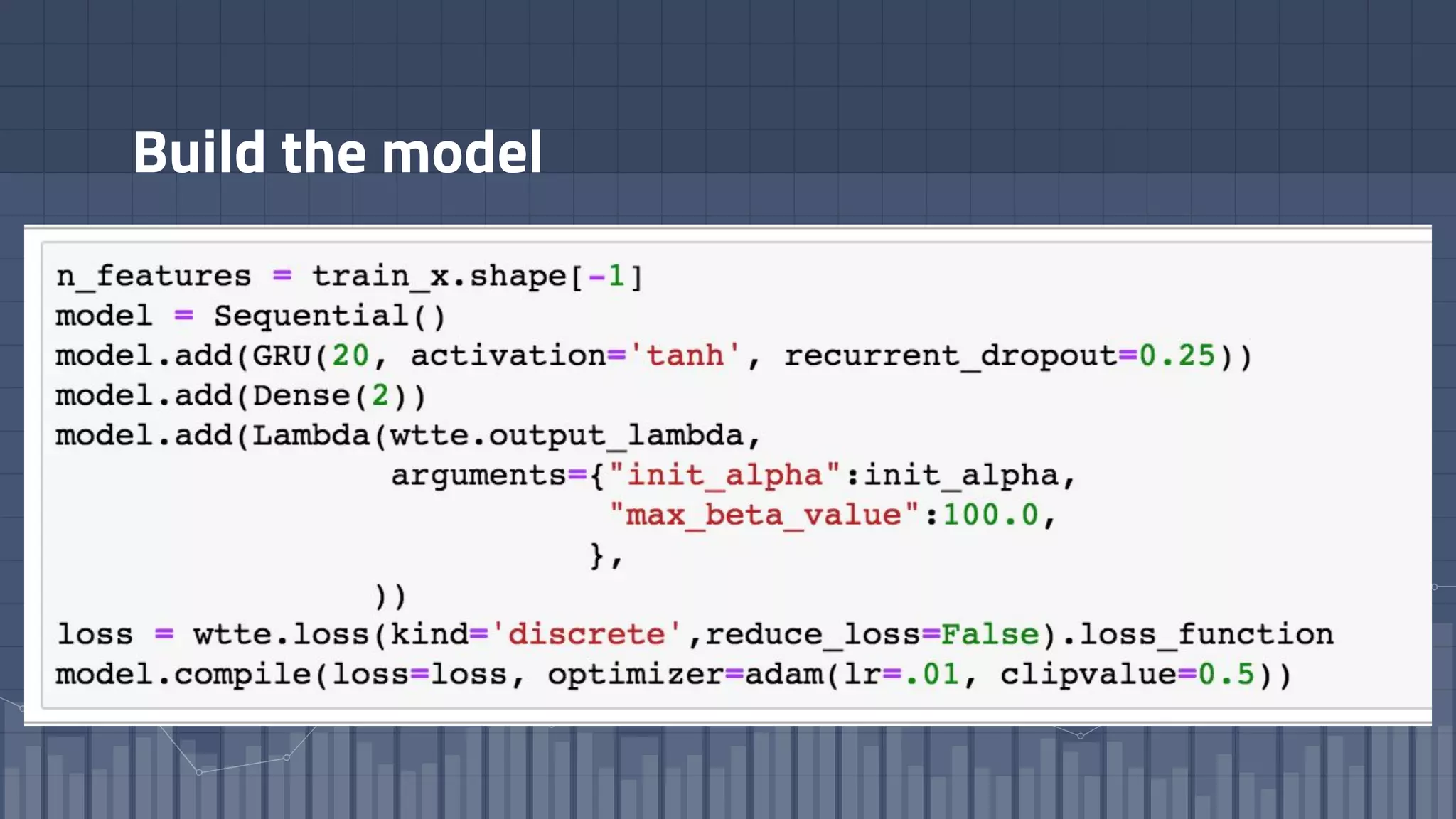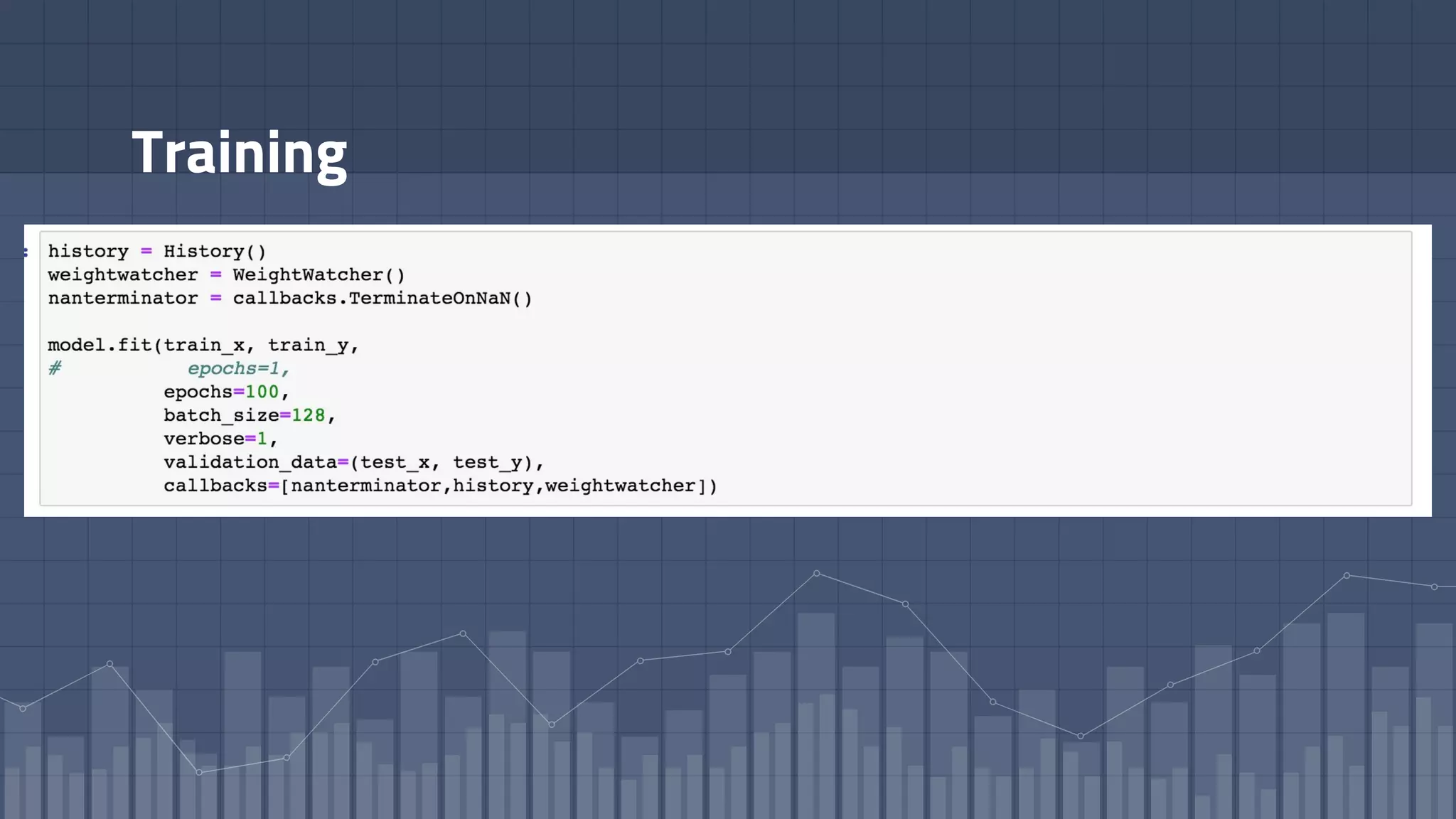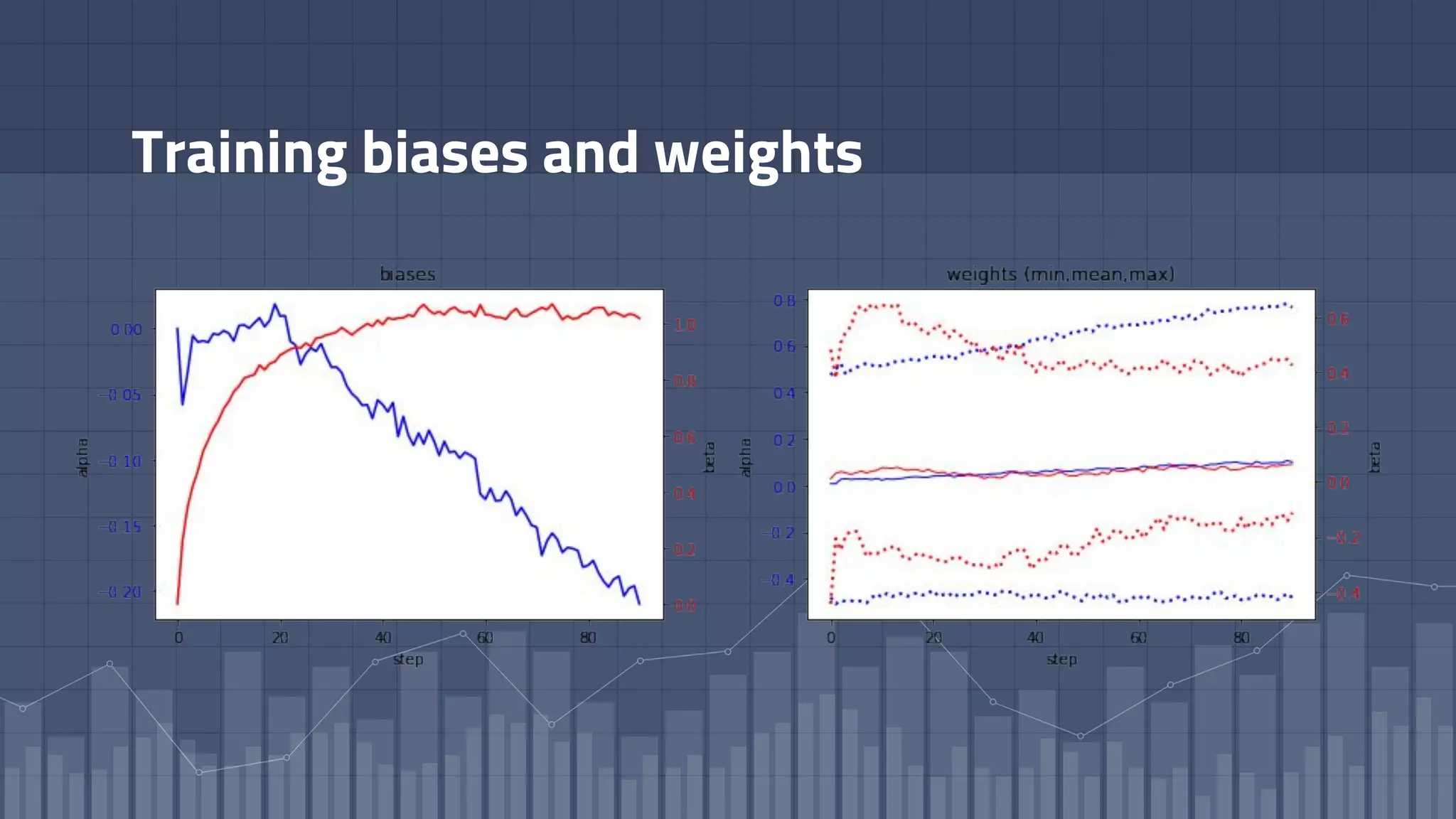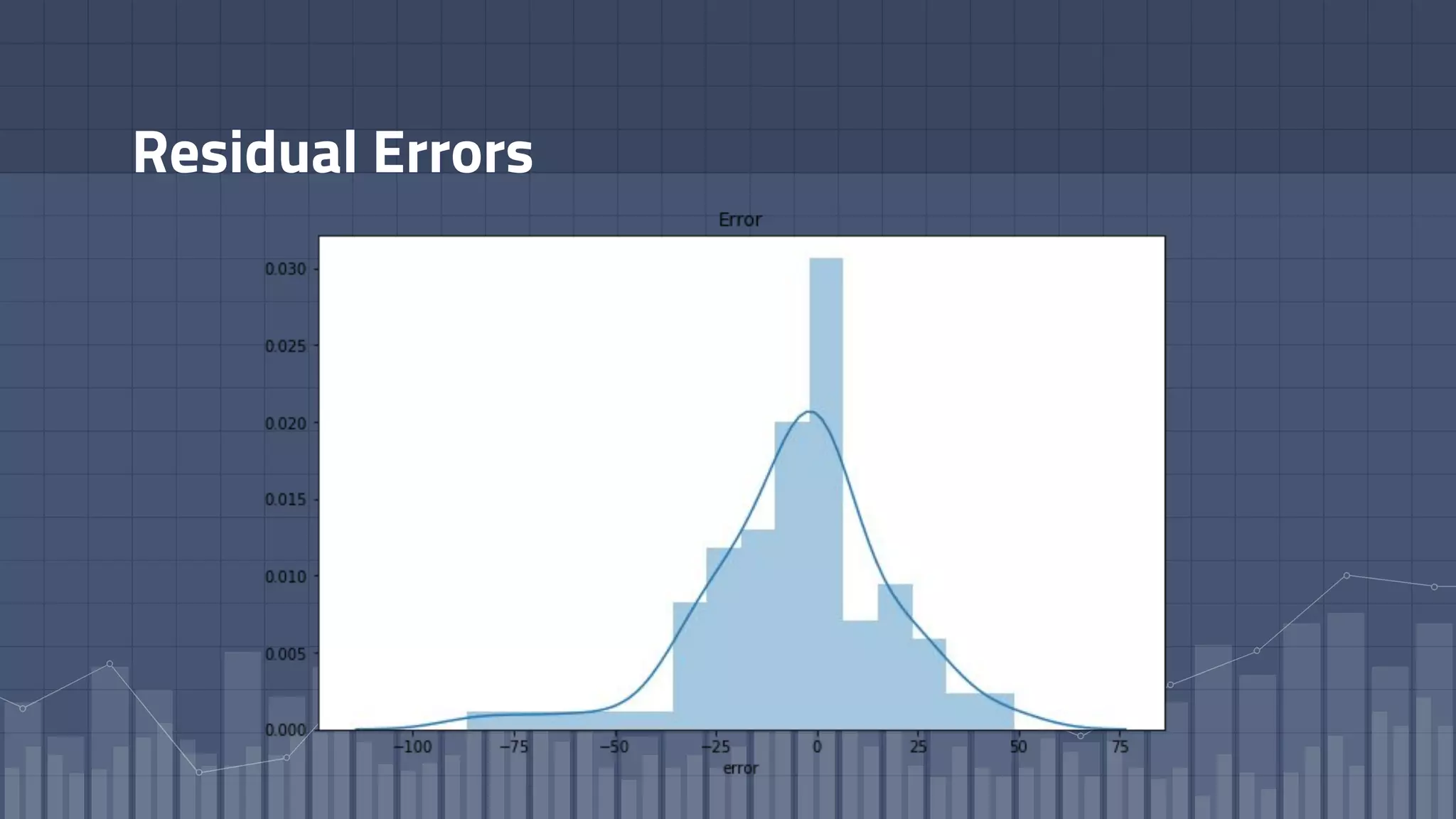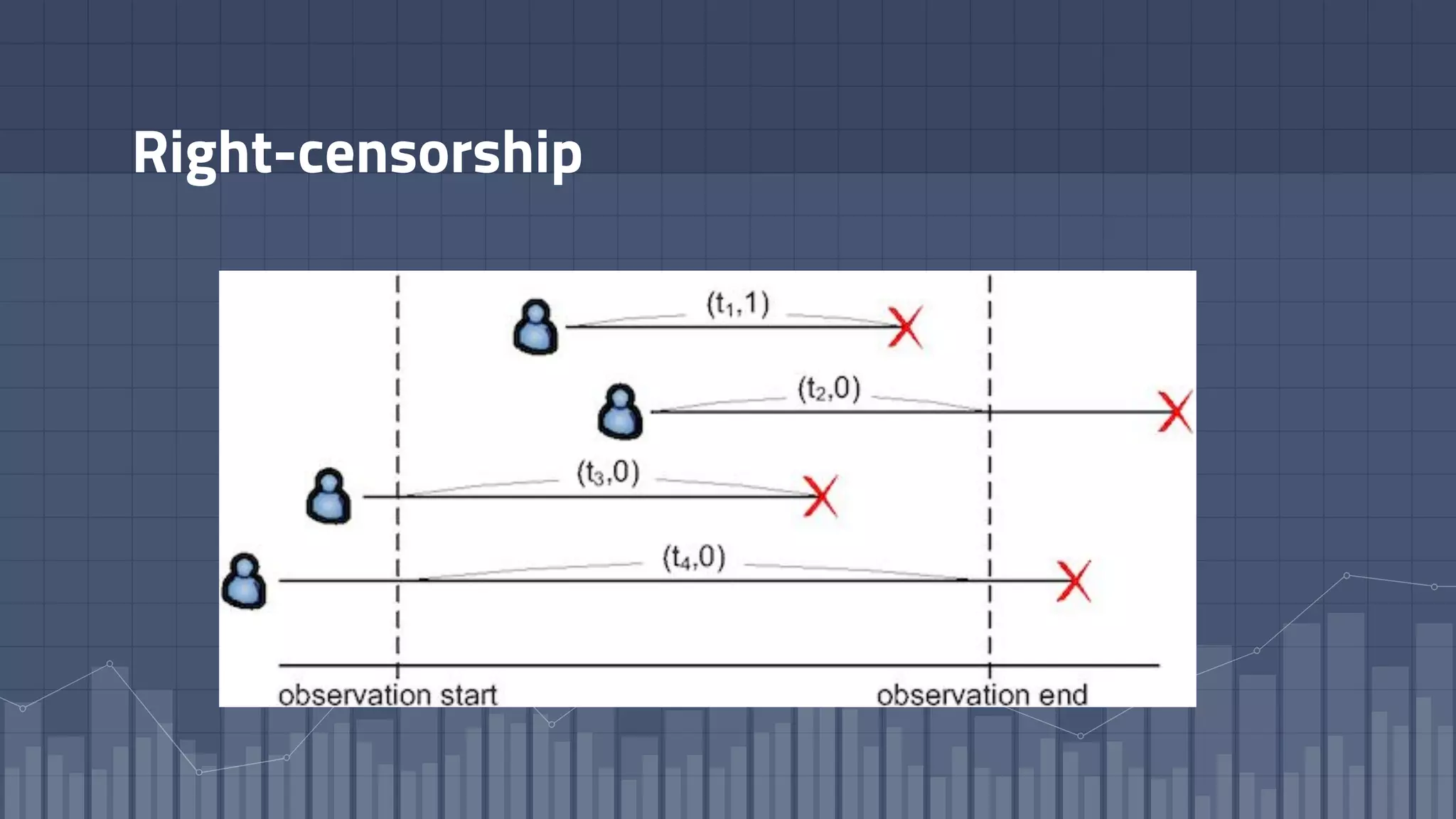3. Key aspects of the Deep Time-to-Failure approach include using censored and uncensored training data, consuming raw time series as input

1. Deep Time-to-Failure
Gianmario Spacagna
IBM #PartyCloud - Data Science Milan meetup
20 September 2018 @ Spirit of Milan

2. Companies main assets
Machineries Customers

3. Bathtub failure curve

4. Data availability (machineries)
▫ Historical time-series of machines sensors telemetry
▫ Registered failures
▫ Active machines real-time measurements

5. Predictive Maintenance

6. Data availability (customers)
▫ Historical sequence of customers behaviours
▫ Stopped subscriptions
▫ Active customers daily activities

7. Churn prediction

8. Time-to-failure events
▫ Patients expected life
▫ Political leadership duration
▫ Product wearing out
▫ Financial default
▫ Employees quitting

9. Data scarcity
▫ Sensors failure (not the machine or user device)
▫ Loss of connectivity
▫ Errors in data collection
▫ IT blackouts
▫ Dropouts
▫ Study termination
▫ Active machine/users not “failed” yet

10. First part
Traditional Survival Analysis

11. Goals
1. Build a model that can estimate the probability
distribution of remaining time-to-failure
2. Train the model by exploiting censored historical data.

12. Right-censorship

13. Survival Function
S(t)=Pr(T>t)
T = failure event time
Probability that the time-to-failure is greater than t

14. Kaplan-Meier estimator
d_i: events happened at time t_i
n_i: known survived individuals
at time t_i

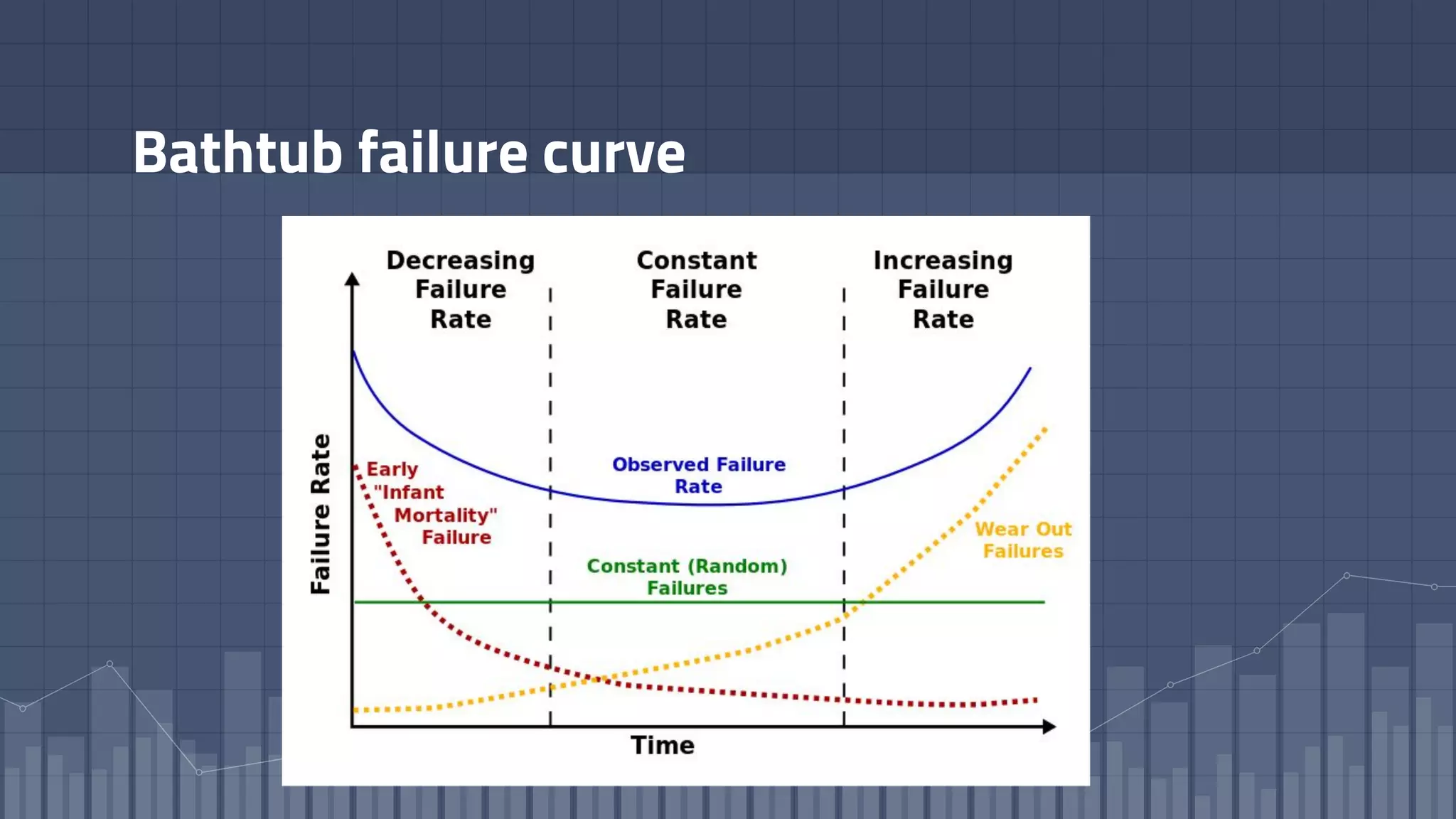
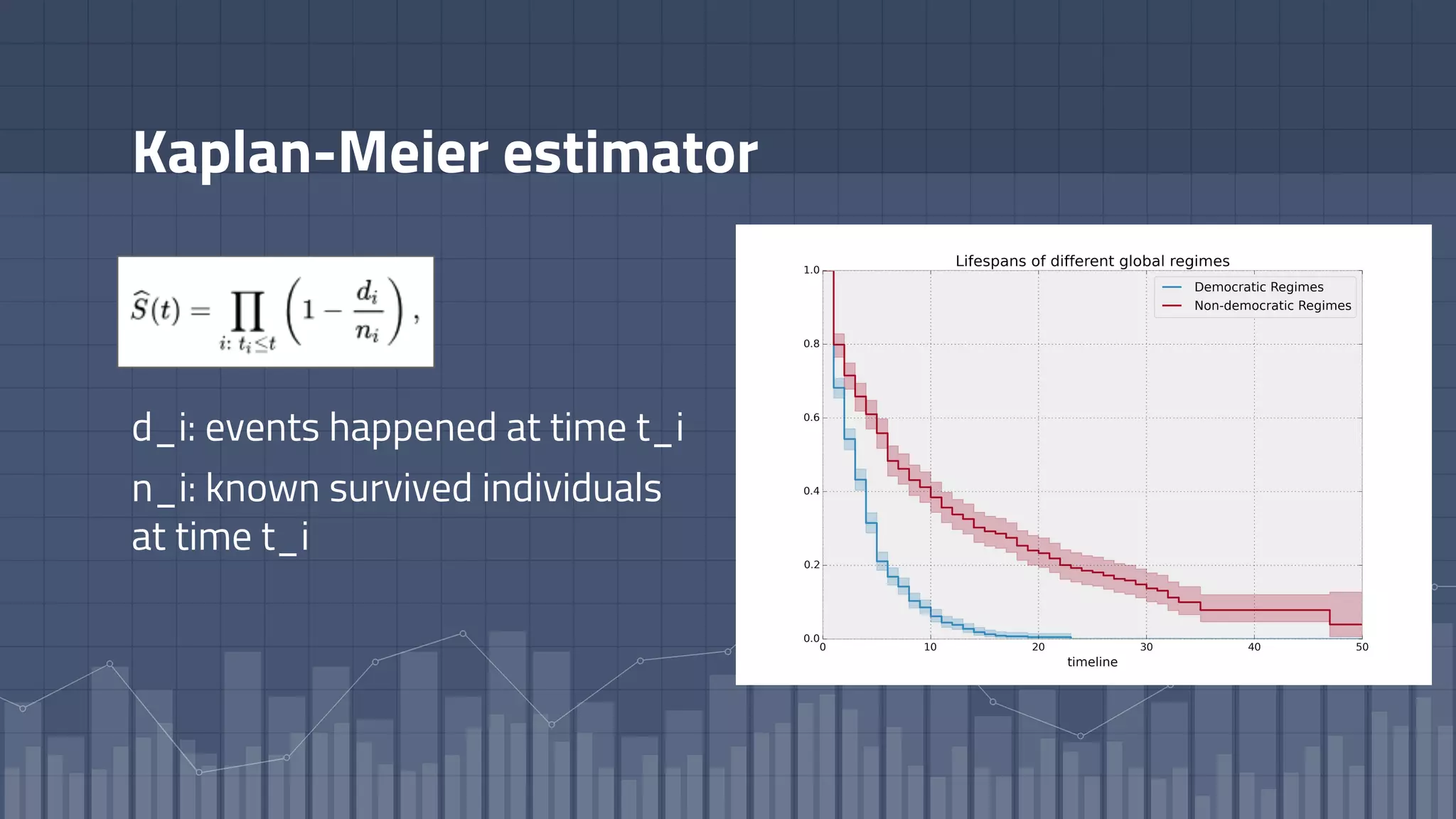
15. Hazard function
h(t) = 𝖯[T= t | T ≥ t]
Probability failure will happen at time t given that we know
it survived up to time t.
Can be interpreted as a measure of the hazard risk, aka.
the probability that failure would happen right now.

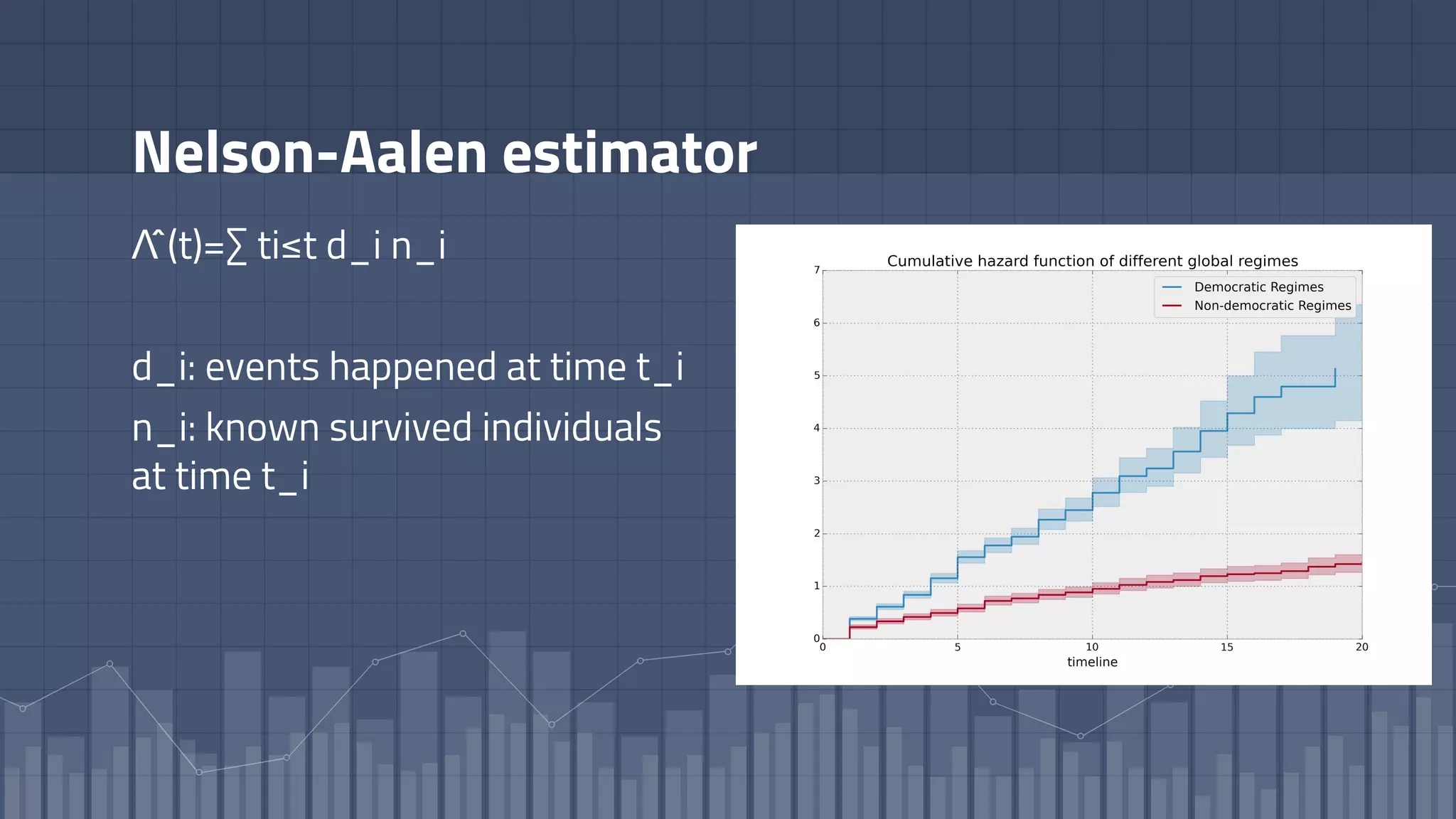
16. Cumulative Hazard function
Λ(t)=∫[0 to t] h(z) dz
Represents the integral of the hazard-rate.

17. Nelson-Aalen estimator
Λ̂ (t)=∑ ti≤t d_i n_i
d_i: events happened at time t_i
n_i: known survived individuals
at time t_i

18. Survival Regression
We have covariates X that we would like to use to map
each individual to his own survival/hazard function.
Features:
● age
● gender
● weight
● is a smoker?
● weekly sport
time?
Model
● Survival function
● Hazard function

19. Cox’s Proportional Hazard model
the log-hazard of an individual is
a linear function of their static
covariates and a population-level
baseline hazard that changes
over time

20. Aalen’s Additive model
The hazard rate is a linear
function of multiple baselines
weighted by their corresponding
covariates

21. Cox’s Time Varying Proportional Hazard
model
If covariates change over time
X(t)

22. Survival Regression
Limitations
▫ Traditional Survival regression models can only
handle categorical or static numerical attributes
▫ Cox’s Time Varying Proportional Hazard model
cannot perform predictions because it would require
to know the future values of covariates
▫ The models do not take into account the sequence of
measurements but only the current statuses
▫ Non-parametric models are hard to generalize

23. Second part
Embrace the Weibull and Deep
Learning euphoria!

24. Weibull Distribution
⍺ = ƛ: scale parameter
β = k: shape parameter

25. Universal PDF for scientists and engineers
Source: https://ragulpr.github.io/2016/12/22/WTTE-RNN-Hackless-churn-modeling/#embrace-the-weibull-euphoria

26. Weibull Time-to-Event Recurrent Neural Net
“An algorithm & philosophy about
predicting when things will happen.”
Egil Martinsson
https://github.com/ragulpr/wtte-rnn

27. Recurrent Neural Networks

28. WTTE-RNN architecture
The output layer consists in
the Weibull parameters

29. Loss function
u = E = 1 censored
u = E = 0 uncensored
Source: https://ragulpr.github.io/assets/draft_master_thesis_martinsson_egil_wtte_rnn_2016.pdf

30. WTTE-RNN in action
Censored
interval

31. Deep Time-to-Failure
▫ Extension of WTTE for failure events
▫ Only one single event to predict (the failure)
▫ Prediction is done at the end of the observed sequence
instead at each step
Failure event
?

32. Case Study: NASA jet engines degradation

33. Raw data

34. Data preparation
Selected 17 relevant features
Values normalized between -1 and 1
Maximum lookback period = 100
Each point corresponded to the subsequence between
time 0 and t up to the failure event
Shorter sequences masked with a special value -99

35. Train/test splits
train_x (20631, 100, 17)
train_y (20631, 2)
test_x (100, 100, 17)
test_y (100, 2)
X contains
axis 0: subsequence identifier
axis 1: time (100 steps)
axis 3: covariate feature
Y contains
axis 0 (T’): latest observation time
axis 1 (E’): 1 if failure event 0 otherwise

36. Training with Censored Data
T = failure time
T'(t) = min(T, t)
E'(t) = if T <= t 1 (observed) else 0 (censored)
Only the full sequence observe the failure,
the other subsequences always have E’ = 0

37. Build the model

38. LSTM Vs. GRU

39. RNN parameters
▫ stateful = False
- each subsequence is independent
▫ return_state=False
- only return the output of the recurrent layer
▫ return_sequences = False
- despite WTTE which is True
- we modeled the problem to give one prediction at
the end of each subsequence instead

40. Initialize alpha and beta
The parameter alpha is proportional to the mean failure
time so we initialize with the mean of observed failures
Beta is a measure of variance so we set max_beta_value
to 100 time steps

41. Output layer activations
Replaced softplus functions from
original paper with:
alpha neuron (a):
alpha = exp(a) * init_alpha
beta neuron(b):
beta= sigmoid(b) * max_beta_value

42. Architecture diagram

43. Trainable parameters

44. Tunable Hyper-parameters
GRU:
▫ activation='tanh'
▫ recurrent_dropout=0.25
▫ dropout=0.3
Optimizer:
▫ algorithm: adam
▫ lr=0.01 (learning_rate)
▫ clipnorm=1

45. Training

46. Loss function over epochs
● Validation loss < training loss
● Test data contains only full
sequences
● easier to predict
● higher accuracy
● lower loss

47. Training biases and weights

48. Inspecting Final Recurrent Activations
Covariates subsequences Hidden activations Output
20 GRUs 2 output
nodes
E
Ground truth
T𝛃𝛂time t
x1
x2
x3
Encoding of the
ith
subsequence
in a 20-dim
vector
x1_i
x2_i
x3_i

49. time t
Inspecting Hidden Recurrent States
x1
x2
x3
20 recurrent states
Output: T, 𝛂, 𝛃
Input covariates
Encoding at
time t_i
t_i
Subsequence
at time t_i
Weibull
parameters
at time t_i
t_i
t_i

50. Debugging nan weights
Can happen if:
▫ beta value too large (e.g. max_beta > 1000)
▫ if needs to reduce beta:
- downscale the time axis
- use shorter sequences
▫ If TensorFlow backend set epsilon to 1e-10
▫ Add a clip_value of 0.5 or less to the optimizer
▫ Clip log-likelihood
▫ Pre-train the output layer (transfer learning)

51. Evaluating global distribution

52. Evaluating last subsequences
Weibull distributions
One curve for each engine
Only last subsequence evaluated
Dots represents expected mode
(maximum likelihood)

53. 𝛃 (∝ variance) Vs. 𝛂 (∝ mean)

54. Precision Vs. T

55. Residual Errors

56. Single engine ttf probability distribution over
time
t
One engine
All of the Weibull distributions
of T estimated at each timestep

57. Single engine T prediction over time
T: time-to-failure
t: current time

58. Conclusions
We learnt a technique deep-ttf which is the extension of
wtte for the specific case of predicting single failures.
The strengths of this approach are:
▫ Consuming raw time-series or sequences
▫ Training with censored and uncensored data
▫ Probabilistic predictions with confidence intervals
▫ Can be applied to any survival regression problem

59. References
Tutorial link: https://github.com/gm-spacagna/deep-ttf
NASA data: https://c3.nasa.gov/dashlink/resources/139/
wtte-rnn: https://github.com/ragulpr/wtte-rnn
Analysis of WTTE-RNN variants that improve
performance, R. Cawley et al.
Recurrent Neural Networks for real-time distributed
collaborative prognostics, A. S. Palau et al.