Simplilearn, profile picture
Uploaded bySimplilearn
2,448 views

Deep Learning Tutorial | Deep Learning TensorFlow | Deep Learning With Neural Networks | Simplilearn

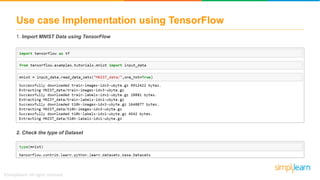
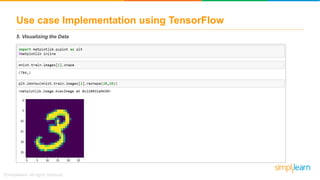
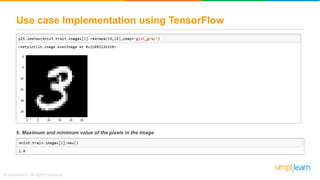
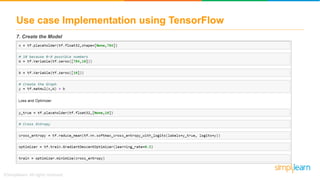
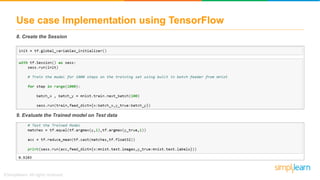
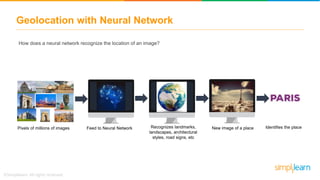
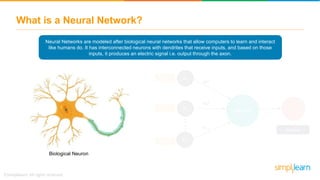
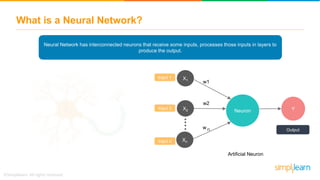
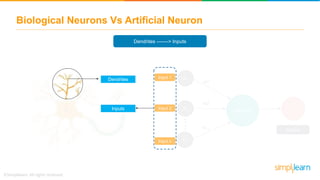
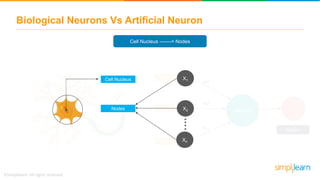
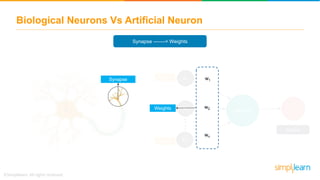
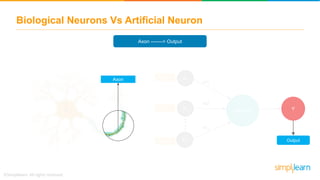
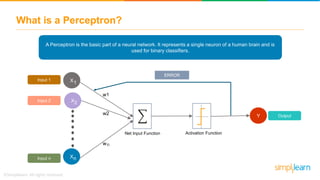
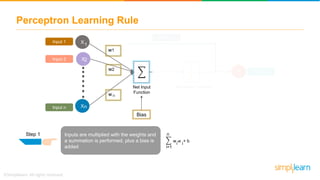
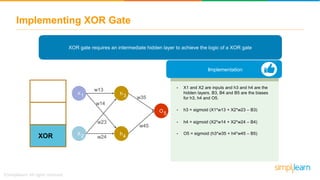
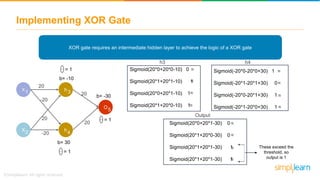
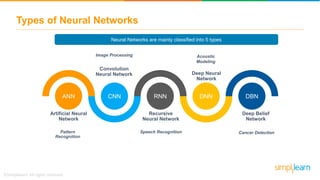
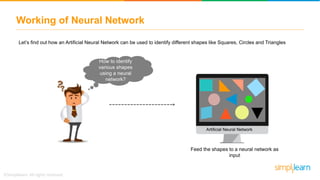
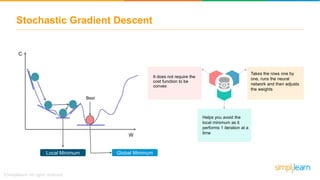
The document discusses how neural networks recognize image locations through geolocation, including the processing of vast image datasets to identify landmarks and architectural features. It explains the functionality and structure of neural networks, including the perceptron model and its ability to perform logical operations. Additionally, it covers various applications of deep learning, how neural networks are implemented, and specifically discusses TensorFlow as a tool for building neural networks.

Education◦
Related topics:
Deep Learning•

Embed presentation

Geolocation with Neural Network How does a neural network recognize the location of an image? Artificial Neural Network New image of a placeImages of millions of places Identifies the place
Geolocation with Neural Network Pixels of millions of images Feed to Neural Network Recognizes landmarks, landscapes, architectural styles, road signs, etc New image of a place Identifies the place How does a neural network recognize the location of an image?
What’s in it for you? Types of Neural Networks Applications of Deep Learning Working of Neural Network Introduction to TensorFlow Use case implementation using TensorFlow What is Deep Learning? What is a Neural Network? Implementing Logic Gates using Perceptron What is a Perceptron? Why do we need Deep Learning?
What is Deep Learning?
What is Deep Learning? Deep Learning is a subset of Machine Learning that has networks which are capable of learning from data that is unstructured or unlabeled and works similar to the functioning of a human brain. Artificial Intelligence Machine Learning Deep Learning Ability of a machine to imitate intelligent human behavior Application of AI that allows a system to automatically learn and improve from experience Application of Machine Learning that uses complex algorithms and deep neural nets to train a model
Why do we need Deep Learning? Machine Learning works only with large sets of structured data, while Deep Learning can work with both structured and unstructured data Deep Learning algorithms can perform complex operations easily while Machine Learning Algorithms cannot Machine Learning algorithms use labelled sample data to extract patterns, while Deep Learning accepts large volumes of data as input, analyze the input to extract features out of an object Performance of Machine Learning algorithms decreases as the amount of data increase, so to maintain the performance of the model we need Deep Learning Works with unstructured data Handle complex operations Feature Extraction Achieve best performance
What is a Neural Network?
What is a Neural Network? Neuron X1 X2 Xn Y Output w1 w2 w n Input 1 Input 2 Input n Neural Networks are modeled after biological neural networks that allow computers to learn and interact like humans do. It has interconnected neurons with dendrites that receive inputs, and based on those inputs, it produces an electric signal i.e. output through the axon. Biological Neuron
What is a Neural Network? Neuron X1 X2 Xn Y Output w1 w2 w n Input 1 Input 2 Input n Neural Network has interconnected neurons that receive some inputs, processes those inputs in layers to produce the output. Artificial Neuron
Biological Neurons Vs Artificial Neuron Dendrites -------> Inputs Neuron X1 X2 Xn Y Output w1 w2 w n Dendrites Input 1 Input 2 Input n Inputs
Biological Neurons Vs Artificial Neuron Cell Nucleus Neuron Input 1 Input 2 Input n Y Output w1 w2 w n Nodes X1 X2 Xn Cell Nucleus -------> Nodes
X1 X2 Xn Biological Neurons Vs Artificial Neuron Synapse Neuron Input 1 Input 2 Input n Y Output Weights w1 w2 wn Synapse -------> Weights
Biological Neurons Vs Artificial Neuron X1 X2 Xn Neuron Input 1 Input 2 Input n w1 w2 wn Axon Axon -------> Output Y Output
What is a Perceptron?
What is a Perceptron? A Perceptron is the basic part of a neural network. It represents a single neuron of a human brain and is used for binary classifiers. X1 X2 Xn Input 1 Input 2 Input n w1 w2 wn Y Output Net Input Function Activation Function ERROR
Perceptron Learning Rule w X1 X2 Xn Input 1 Input 2 Input n w2 Y Output Activation Function ERROR w1 n Net Input Function Inputs are multiplied with the weights and a summation is performed, plus a bias is added Bias i=1 n w x + b i i* Step 1
Perceptron Learning Rule w X1 X2 Xn Input 1 Input 2 Input n w2 Y Output Activation Function ERROR w1 n Net Input Function The weighted sum of inputs is passed to an activation function to determine if a neuron will fire or not Step 2
Perceptron Learning Rule w X1 X2 Xn Input 1 Input 2 Input n w2 Y Output Activation Function ERROR w1 n Net Input Function Perceptron receives input signals and if the sum of the input signals exceeds a certain threshold value, it either outputs a signal or does not return an output Output = 0, if i=1 n w x + b < threshold i i* 1, if i=1 n w x + b >= thresholdi i* Step 3
Perceptron Learning Rule w X1 X2 Xn Input 1 Input 2 Input n w2 Y Output Activation Function ERROR w1 n Net Input Function The error in the output is backpropagated and weights are updated to minimize the error Step 4
Perceptron Learning Rule w X1 X2 Xn Input 1 Input 2 Input n w2 Y Output Activation Function ERROR w1 n Net Input Function Repeat steps 1 to 4 in order to generate the desired output
Implementing Logic Gates using Perceptron In 1943, neuroscientist Warren McCulloch and logician Walter Pitts published a paper showing how neurons could implement the three logical functions (AND, OR, XOR). The neurons they used were simple threshold neurons which they named it Perceptron. Warren McCulloch Walter Pitts
Implementing Logic Gates using Perceptron A logic gate is the basic building block of a digital circuit. Most logic gates have 2 inputs and 1 output. At any given moment, every terminal is in one of the two binary conditions low (0) or high (1), represented by different voltage levels. Popular Logic Gates AND OR NAND NOR NOT XOR
Implementing AND Gate Using the Logic Gates, Neural Networks can learn on their own without having to manually code the logic Input (A) Input (B) Output 0 0 0 0 1 0 1 0 0 1 1 1 AND The output of Perceptron is true or positive if both the inputs are true, else false
Implementing AND Gate A and B are input neurons. The red neuron is our output neuron. The threshold value is 1. If the sum of the weighted input neurons is greater than the threshold, the output is 1 else 0. Input (A) Input (B) Output 0.7*0 0.7*0 0 0.7*0 0.7*1 0.7 0.7*1 0.7*0 0.7 0.7*1 0.7*1 1.4 A B 0.7 0.7 = 1 This exceeds the threshold, so output is 1 We have designed a neuron which implements a logical AND gate w x1 1* w x 2 2* w x +1 1* w x 2 2*
Implementing OR Gate Using the Logic Gates, Neural Networks can learn on their own without having to manually code the logic Input (A) Input (B) Output 0 0 0 0 1 1 1 0 1 1 1 1 OR The output of Perceptron is true or positive if either of the inputs are true, else false
Implementing OR Gate A and B are input neurons. The red neuron is our output neuron. The threshold value is 1. If the sum of the weighted input neurons is greater than the threshold, the output is 1 else 0. Input (A) Input (B) Output 1.2*0 1.2*0 0 1.2*0 1.2*1 1.2 1.2*1 1.2*0 1.2 1.2*1 1.2*1 2.4 A B 1.2 1.2 = 1 These exceed the threshold, so output is 1 w x1 1* w x 2 2* w x +1 1* w x 2 2* We have designed a neuron which implements a logical OR gate
Implementing XOR Gate Using the Logic Gates, Neural Networks can learn on their own without having to manually code the logic Input (A) Input (B) Output 0 0 0 0 1 1 1 0 1 1 1 0 XOR The output of Perceptron is true or positive if one of the inputs is true, else false
Implementing XOR Gate XOR gate requires an intermediate hidden layer to achieve the logic of a XOR gate XOR Implementation 5 X X h h O 1 2 3 4 w13 w14 w23 w24 w45 w35 5 • X1 and X2 are inputs and h3 and h4 are the hidden layers. B3, B4 and B5 are the biases for h3, h4 and O5. • h3 = sigmoid (X1*w13 + X2*w23 – B3) • h4 = sigmoid (X2*w14 + X2*w24 – B4) • O5 = sigmoid (h3*w35 + h4*w45 – B5)
Implementing XOR Gate XOR gate requires an intermediate hidden layer to achieve the logic of a XOR gate 5 X X h h O 1 2 3 4 20 -20 20 -20 20 20 5 Sigmoid(20*0+20*0-10) 0 Sigmoid(20*1+20*1-10) 1 Sigmoid(20*0+20*1-10) 1 Sigmoid(20*1+20*0-10) 1 ~~ ~~ ~~ ~~ Sigmoid(-20*0-20*0+30) 1 Sigmoid(-20*1-20*1+30) 0 Sigmoid(-20*0-20*1+30) 1 Sigmoid(-20*1-20*0+30) 1 ~~ ~~ ~~ ~~ b= -10 Sigmoid(20*0+20*1-30) 0 Sigmoid(20*1+20*0-30) 0 Sigmoid(20*1+20*1-30) 1 Sigmoid(20*1+20*1-30) 1 ~~ ~~ ~~ ~~ h3 h4 Output These exceed the threshold, so output is 1 b= 30 b= -30 = 1 = 1 = 1
Types of Neural Network
Types of Neural Networks Pattern Recognition ANN CNN RNN DNN DBN Image Processing Acoustic Modeling Recursive Neural Network Cancer Detection Neural Networks are mainly classified into 5 types Artificial Neural Network Convolution Neural Network Speech Recognition Deep Neural Network Deep Belief Network
Applications of Deep Learning
Applications of Deep Learning Deep Learning allows us to build machines that can play games Playing Games
Applications of Deep Learning Composing Music Deep Neural Nets can be used to produce music by making computers learn the patterns in a composition
Applications of Deep Learning Autonomous Driving Cars Distinguishes different types of objects, people, road signs and drives without human intervention
Applications of Deep Learning Building Robots Deep Learning is used to train robots to perform human tasks
Applications of Deep Learning Medical Diagnosis Deep Neural Nets are used to identify suspicious lesions and nodules in lung cancer patients
Working of Neural Network
Working of Neural Network Let’s find out how an Artificial Neural Network can be used to identify different shapes like Squares, Circles and Triangles How to identify various shapes using a neural network? Feed the shapes to a neural network as input Artificial Neural Network
Working of Neural Network Artificial Neural Network 28 28 Strengths 28 28 = 784* • 28*28 pixels of the input image is taken as input i.e. 784 neurons Lets consider the shape of a square Shape of a Square
Working of Neural Network 28 28 Strengths • 28*28 pixels of the input image is taken as input i.e. 784 neurons 28 28 = 784* 0.78 Activation • Each neuron holds a number called Activation that represents grayscale value of the corresponding pixel ranging from 0 to 1. 1 for white pixel and 0 for black pixel Lets consider the shape of a square Artificial Neural Network
Working of Neural Network Lets consider the shape of a square 28 28 Strengths • 28*28 pixels of the input image is taken as input i.e. 784 neurons • Each neuron is lit up when its activation is close to 1 28 28 = 784* • Each neuron holds a number called Activation that represents grayscale value of the corresponding pixel ranging from 0 to 1. 1 for white pixel and 0 for black pixel Artificial Neural Network
Working of Neural Network
Working of Neural Network
Working of Neural Network
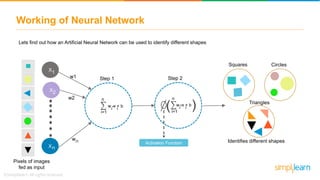
Working of Neural Network X1 X2 Xn w1 w2 wn Step 1 i=1 n w x + b i i* Activation Function Step 2 i=1 n w x + b ii*( ) Lets find out how an Artificial Neural Network can be used to identify different shapes Identifies different shapes Squares Circles Triangles Pixels of images fed as input
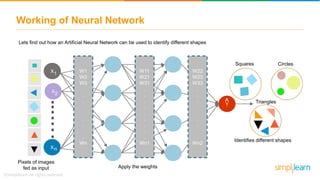
Working of Neural Network Lets find out how an Artificial Neural Network can be used to identify different shapes X1 X2 Xn Y W1 W2 W3 . . . . . . . . . Wn W22 W23 W33 . . . . . . . . . Wn2 W11 W21 W31 . . . . . . . . . Wn1 Apply the weights Identifies different shapes Squares Circles Triangles^ Pixels of images fed as input
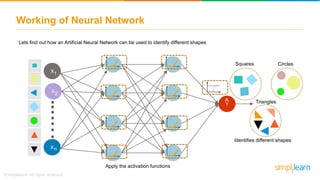
Working of Neural Network Lets find out how an Artificial Neural Network can be used to identify different shapes X1 X2 Xn Y^ Apply the activation functions Identifies different shapes Squares Circles Triangles
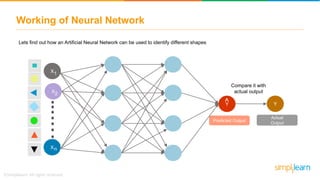
Working of Neural Network Lets find out how an Artificial Neural Network can be used to identify different shapes X1 X2 Xn Y^ Compare it with actual output Predicted Output Actual Output Y
Working of Neural Network Applying the cost function to minimize the difference between predicted and actual output using gradient descent algorithm Predicted Output X1 X2 Xn Y^ Actual Output Compare it with actual output Y Cost Function: C = ½( Y – Y ) 2
Working of Neural Network Neural Networks use Backpropagation method along with improve the performance of the Neural Net. A cost function is used to reduce the error rate between predicted and actual output. X X X Y^ Cost Function: C = ½( Y – Y ) 2 1 2 n Y
Cost Function The Cost value is the difference between the neural nets predicted output and the actual output from a set of labelled training data. The least cost value is obtained by making adjustments to the weights and biases iteratively throughout the training process. X X Xn Y Y^ W1 W2 W3 . . . . . . . . . Wn W22 W23 W33 . . . . . . . . . Wn2 W11 W21 W31 . . . . . . . . . Wn1 1 2 Cost Function: C = ½( Y – Y ) 2
Gradient Descent Slower Faster The person will take more time to reach the base of the mountain if the slope is gentle and will come down faster if the slope is steep. Likewise, a Neural Net will train slowly if the Gradient is small and it will train quickly if the Gradient is large. Gradient Descent is an optimization algorithm for finding the minimum of a function A person trying to reach the base of a mountain
Gradient Descent Gradient Descent is an optimization algorithm for finding the minimum of a functionGradient Descent is an optimization algorithm for finding the minimum of a function C = ½( Y – Y )^ 2 C W C W Best Gradient Global Minimum cost Initial Weight
Stochastic Gradient Descent C W Best Local Minimum Global Minimum It does not require the cost function to be convex Takes the rows one by one, runs the neural network and then adjusts the weights Helps you avoid the local minimum as it performs 1 iteration at a time
Deep Learning Platforms Torch Keras 4 main platforms TensorFlow DeepLearning4J (java)
Introduction to TensorFlow
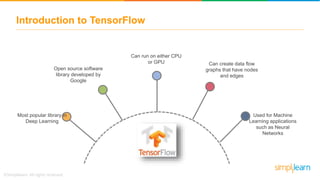
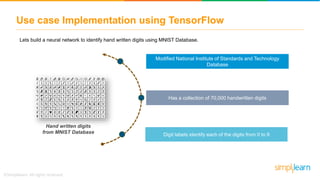
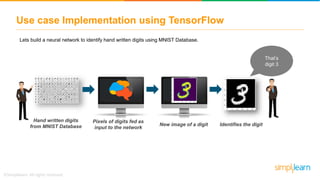
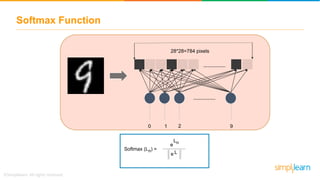
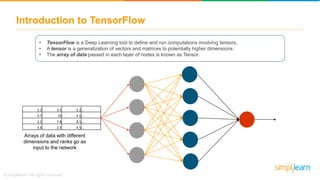
Introduction to TensorFlow • TensorFlow is a Deep Learning tool to define and run computations involving tensors. • A tensor is a generalization of vectors and matrices to potentially higher dimensions. • The array of data passed in each layer of nodes is known as Tensor. a m k q d 2 4 8 1 1 9 3 2 5 4 4 6 6 3 3 7 8 2 9 5 Tensor of Dimensions[5] Tensor of Dimensions[5,4]Tensor of Dimension[3,3,3]
Introduction to TensorFlow • TensorFlow is a Deep Learning tool to define and run computations involving tensors. • A tensor is a generalization of vectors and matrices to potentially higher dimensions. • The array of data passed in each layer of nodes is known as Tensor. 1.2 3.5 2.2… 4.7 10 4.5… 2.2 7.8 8.1… 3.6 2.5 4.5… Arrays of data with different dimensions and ranks go as input to the network
Tensor Ranks m=V=[1,2,3],[4,5,6] v=[10,20,30] t=[[[1],[2],[3]],[[4],[5],[6]],[[7],[8],[9]]] s= [107] Tensor of Rank 0 Tensor of Rank 1 Tensor of Rank 2Tensor of Rank 3
Introduction to TensorFlow Open source software library developed by Google Most popular library in Deep Learning Can run on either CPU or GPU Can create data flow graphs that have nodes and edges Used for Machine Learning applications such as Neural Networks
Use case Implementation using TensorFlow Lets build a neural network to identify hand written digits using MNIST Database. Hand written digits from MNIST Database Modified National Institute of Standards and Technology Database Has a collection of 70,000 handwritten digits Digit labels identify each of the digits from 0 to 9
Use case Implementation using TensorFlow Lets build a neural network to identify hand written digits using MNIST Database. Hand written digits from MNIST Database Pixels of digits fed as input to the network New image of a digit Identifies the digit That’s digit 3
Softmax Function ……………. 0 1 2 9 28*28=784 pixels ……………. Softmax (Ln) = Ln e e L
Use case Implementation using TensorFlow 1. Import MNIST Data using TensorFlow 2. Check the type of Dataset
Use case Implementation using TensorFlow 3. Array of Training images 4. Number of images for Training, Testing and Validation
Use case Implementation using TensorFlow 5. Visualizing the Data
Use case Implementation using TensorFlow 6. Maximum and minimum value of the pixels in the image
Use case Implementation using TensorFlow 7. Create the Model
Use case Implementation using TensorFlow 8. Create the Session 9. Evaluate the Trained model on Test data
Deep Learning Tutorial | Deep Learning TensorFlow | Deep Learning With Neural Networks | Simplilearn

More Related Content

PPTX
Deep Learning Tutorial | Deep Learning Tutorial For Beginners | What Is Deep ...
bySimplilearn
 
PPTX
Intro to deep learning
byDavid Voyles
 
PPTX
Artificial Neural Network | Deep Neural Network Explained | Artificial Neural...
bySimplilearn
 
PPTX
Deep Learning Applications | Deep Learning Applications In Real Life | Deep l...
bySimplilearn
 
PPTX
Deep Learning Tutorial
byAmr Rashed
 
PPTX
What Is A Neural Network? | How Deep Neural Networks Work | Neural Network Tu...
bySimplilearn
 
PDF
Deep learning
byAlessio Palma
 
PDF
Introduction to Deep learning
byMassimiliano Ruocco
 
Deep Learning Tutorial | Deep Learning Tutorial For Beginners | What Is Deep ...
bySimplilearn
 
Intro to deep learning
byDavid Voyles
 
Artificial Neural Network | Deep Neural Network Explained | Artificial Neural...
bySimplilearn
 
Deep Learning Applications | Deep Learning Applications In Real Life | Deep l...
bySimplilearn
 
Deep Learning Tutorial
byAmr Rashed
 
What Is A Neural Network? | How Deep Neural Networks Work | Neural Network Tu...
bySimplilearn
 
Deep learning
byAlessio Palma
 
Introduction to Deep learning
byMassimiliano Ruocco
 

What's hot

PDF
Deep learning - A Visual Introduction
byLukas Masuch
 
PPTX
What Is Deep Learning? | Introduction to Deep Learning | Deep Learning Tutori...
bySimplilearn
 
PDF
An introduction to Deep Learning
byJulien SIMON
 
PDF
Deep Learning - Overview of my work II
byMohamed Loey
 
PDF
An Introduction to Deep Learning
byPoo Kuan Hoong
 
PDF
Introduction to Neural Networks
byDatabricks
 
PPTX
Recurrent Neural Network (RNN) | RNN LSTM Tutorial | Deep Learning Course | S...
bySimplilearn
 
PPTX
Introduction to Deep learning
byleopauly
 
PPTX
Generative Adversarial Network (GAN)
byPrakhar Rastogi
 
PDF
Convolutional neural network
byYan Xu
 
PPTX
Introduction to Deep Learning
byOswald Campesato
 
PPTX
Artifical Neural Network and its applications
bySangeeta Tiwari
 
PDF
Introduction to Recurrent Neural Network
byKnoldus Inc.
 
PPTX
Deep learning with tensorflow
byCharmi Chokshi
 
PDF
Neural networks and deep learning
byJörgen Sandig
 
PPTX
Convolutional neural network
byMojammilHusain
 
PPTX
Introduction For seq2seq(sequence to sequence) and RNN
byHye-min Ahn
 
PPTX
Introduction Of Artificial neural network
byNagarajan
 
PDF
Introduction of Deep Learning
byMyungjin Lee
 
PDF
Deep Feed Forward Neural Networks and Regularization
byYan Xu
 
Deep learning - A Visual Introduction
byLukas Masuch
 
What Is Deep Learning? | Introduction to Deep Learning | Deep Learning Tutori...
bySimplilearn
 
An introduction to Deep Learning
byJulien SIMON
 
Deep Learning - Overview of my work II
byMohamed Loey
 
An Introduction to Deep Learning
byPoo Kuan Hoong
 
Introduction to Neural Networks
byDatabricks
 
Recurrent Neural Network (RNN) | RNN LSTM Tutorial | Deep Learning Course | S...
bySimplilearn
 
Introduction to Deep learning
byleopauly
 
Generative Adversarial Network (GAN)
byPrakhar Rastogi
 
Convolutional neural network
byYan Xu
 
Introduction to Deep Learning
byOswald Campesato
 
Artifical Neural Network and its applications
bySangeeta Tiwari
 
Introduction to Recurrent Neural Network
byKnoldus Inc.
 
Deep learning with tensorflow
byCharmi Chokshi
 
Neural networks and deep learning
byJörgen Sandig
 
Convolutional neural network
byMojammilHusain
 
Introduction For seq2seq(sequence to sequence) and RNN
byHye-min Ahn
 
Introduction Of Artificial neural network
byNagarajan
 
Introduction of Deep Learning
byMyungjin Lee
 
Deep Feed Forward Neural Networks and Regularization
byYan Xu
 

Similar to Deep Learning Tutorial | Deep Learning TensorFlow | Deep Learning With Neural Networks | Simplilearn

PPS
Neural Networks Ver1
byncct
 
PPT
2011 0480.neural-networks
byParneet Kaur
 
PPTX
lecture13-NN-basics.pptx
byAbijahRoseline1
 
PPTX
Neural-Networks.................................................................
byguru559911
 
PDF
Lecture7_Neural Networks_and_analysis2024.pdf
byadiworks30
 
PDF
Unit-2.3 NN.pdf deep nural network pdf by Dr.Ravinder singh (Professor)
byTarunYadav236535
 
PPT
SOFT COMPUTERING TECHNICS -Unit 1
bysravanthi computers
 
PDF
Neural Networks_Example.Neural Networks_Example.
byankitashah717131
 
PDF
SURVEY ON BRAIN – MACHINE INTERRELATIVE LEARNING
byIRJET Journal
 
PPT
Soft Computering Technics - Unit2
bysravanthi computers
 
PPT
ComputationalIntelligence_Lect2_ANeuralNetworks.ppt
byAlnoorIbrahim1
 
DOCX
Neural networks of artificial intelligence
byalldesign
 
PPT
Neural networks 1
byVaibhav Shah
 
PPTX
Deep learning Ann(Artificial neural network)
byaawezix
 
PPTX
1.Introduction to Artificial Neural Networks.pptx
bysalahidddin
 
PPTX
1.Introduction to Artificial Neural Networks.pptx
bysalahidddin
 
PPS
Neural Networks
byIsmail El Gayar
 
PPTX
softcomputing.pptx
byKaviya452563
 
PDF
Artificial Neural Network
byssuserab4f3e
 
PPT
The Introduction to Neural Networks.ppt
bymoh2020
 
Neural Networks Ver1
byncct
 
2011 0480.neural-networks
byParneet Kaur
 
lecture13-NN-basics.pptx
byAbijahRoseline1
 
Neural-Networks.................................................................
byguru559911
 
Lecture7_Neural Networks_and_analysis2024.pdf
byadiworks30
 
Unit-2.3 NN.pdf deep nural network pdf by Dr.Ravinder singh (Professor)
byTarunYadav236535
 
SOFT COMPUTERING TECHNICS -Unit 1
bysravanthi computers
 
Neural Networks_Example.Neural Networks_Example.
byankitashah717131
 
SURVEY ON BRAIN – MACHINE INTERRELATIVE LEARNING
byIRJET Journal
 
Soft Computering Technics - Unit2
bysravanthi computers
 
ComputationalIntelligence_Lect2_ANeuralNetworks.ppt
byAlnoorIbrahim1
 
Neural networks of artificial intelligence
byalldesign
 
Neural networks 1
byVaibhav Shah
 
Deep learning Ann(Artificial neural network)
byaawezix
 
1.Introduction to Artificial Neural Networks.pptx
bysalahidddin
 
1.Introduction to Artificial Neural Networks.pptx
bysalahidddin
 
Neural Networks
byIsmail El Gayar
 
softcomputing.pptx
byKaviya452563
 
Artificial Neural Network
byssuserab4f3e
 
The Introduction to Neural Networks.ppt
bymoh2020
 

More from Simplilearn

PPTX
Top 50 Scrum Master Interview Questions | Scrum Master Interview Questions & ...
bySimplilearn
 
PPTX
Bagging Vs Boosting In Machine Learning | Ensemble Learning In Machine Learni...
bySimplilearn
 
PPTX
Future Of Social Media | Social Media Trends and Strategies 2025 | Instagram ...
bySimplilearn
 
PPTX
SQL Query Optimization | SQL Query Optimization Techniques | SQL Basics | SQL...
bySimplilearn
 
PPTX
SQL INterview Questions .pTop 45 SQL Interview Questions And Answers In 2025 ...
bySimplilearn
 
PPTX
How To Start Influencer Marketing Business | Influencer Marketing For Beginne...
bySimplilearn
 
PPTX
Cyber Security Roadmap 2025 | How To Become Cyber Security Engineer In 2025 |...
bySimplilearn
 
PPTX
How To Become An AI And ML Engineer In 2025 | AI Engineer Roadmap | AI ML Car...
bySimplilearn
 
PPTX
What Is GitHub Copilot? | How To Use GitHub Copilot? | How does GitHub Copilo...
bySimplilearn
 
PPTX
Top 10 Data Analyst Certification For 2025 | Best Data Analyst Certification ...
bySimplilearn
 
PPTX
Complete Data Science Roadmap For 2025 | Data Scientist Roadmap For Beginners...
bySimplilearn
 
PPTX
Top 7 High Paying AI Certifications Courses For 2025 | Best AI Certifications...
bySimplilearn
 
PPTX
Data Cleaning In Data Mining | Step by Step Data Cleaning Process | Data Clea...
bySimplilearn
 
PPTX
Top 10 Data Analyst Projects For 2025 | Data Analyst Projects | Data Analysis...
bySimplilearn
 
PPTX
AI Engineer Roadmap 2025 | AI Engineer Roadmap For Beginners | AI Engineer Ca...
bySimplilearn
 
PPTX
Machine Learning Roadmap 2025 | Machine Learning Engineer Roadmap For Beginne...
bySimplilearn
 
PPTX
Kotter's 8-Step Change Model Explained | Kotter's Change Management Model | S...
bySimplilearn
 
PPTX
Gen AI Engineer Roadmap For 2025 | How To Become Gen AI Engineer In 2025 | Si...
bySimplilearn
 
PPTX
Top 10 Data Analyst Certification For 2025 | Best Data Analyst Certification ...
bySimplilearn
 
PPTX
Complete Data Science Roadmap For 2025 | Data Scientist Roadmap For Beginners...
bySimplilearn
 
Top 50 Scrum Master Interview Questions | Scrum Master Interview Questions & ...
bySimplilearn
 
Bagging Vs Boosting In Machine Learning | Ensemble Learning In Machine Learni...
bySimplilearn
 
Future Of Social Media | Social Media Trends and Strategies 2025 | Instagram ...
bySimplilearn
 
SQL Query Optimization | SQL Query Optimization Techniques | SQL Basics | SQL...
bySimplilearn
 
SQL INterview Questions .pTop 45 SQL Interview Questions And Answers In 2025 ...
bySimplilearn
 
How To Start Influencer Marketing Business | Influencer Marketing For Beginne...
bySimplilearn
 
Cyber Security Roadmap 2025 | How To Become Cyber Security Engineer In 2025 |...
bySimplilearn
 
How To Become An AI And ML Engineer In 2025 | AI Engineer Roadmap | AI ML Car...
bySimplilearn
 
What Is GitHub Copilot? | How To Use GitHub Copilot? | How does GitHub Copilo...
bySimplilearn
 
Top 10 Data Analyst Certification For 2025 | Best Data Analyst Certification ...
bySimplilearn
 
Complete Data Science Roadmap For 2025 | Data Scientist Roadmap For Beginners...
bySimplilearn
 
Top 7 High Paying AI Certifications Courses For 2025 | Best AI Certifications...
bySimplilearn
 
Data Cleaning In Data Mining | Step by Step Data Cleaning Process | Data Clea...
bySimplilearn
 
Top 10 Data Analyst Projects For 2025 | Data Analyst Projects | Data Analysis...
bySimplilearn
 
AI Engineer Roadmap 2025 | AI Engineer Roadmap For Beginners | AI Engineer Ca...
bySimplilearn
 
Machine Learning Roadmap 2025 | Machine Learning Engineer Roadmap For Beginne...
bySimplilearn
 
Kotter's 8-Step Change Model Explained | Kotter's Change Management Model | S...
bySimplilearn
 
Gen AI Engineer Roadmap For 2025 | How To Become Gen AI Engineer In 2025 | Si...
bySimplilearn
 
Top 10 Data Analyst Certification For 2025 | Best Data Analyst Certification ...
bySimplilearn
 
Complete Data Science Roadmap For 2025 | Data Scientist Roadmap For Beginners...
bySimplilearn
 

Recently uploaded

PPTX
Alma Šuto - From Tradition to Innovation: Creative AI in Education
bybvtricks
 
PDF
Take This Quirky Quiz! - QGI 1st Anniversary .pdf
byNiyati Jois
 
PPTX
Fruit Fermentation_ Ethanol & Sugar Estimation- Dr. Shikha Gaikwad
byinsighteduwithme
 
PDF
Infrared Spectroscopy (IR spectroscopy).ppt
byLife sciences
 
PPTX
Central Line Associated Bloodstream Infection
bynabinabhaila40
 
PDF
Oscillations /Revision notes prepared by K sandeep swamy (Msc,BEd)/For online...
bySandeep Swamy
 
PPTX
Statistical Data Analysis using R Programming.pptx
byVETRISELVIP1
 
PDF
ĐỀ MINH HỌA KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2026 MÔN TIẾNG ANH 2026...
byNguyen Thanh Tu Collection
 
PPTX
Day 2 ppt english.powerpoint presentation ppt
byJeahMaeMedez
 
PPTX
NMR Spectroscopy: Principles and Applications
byVanitha Rajakumar
 
PDF
Beak Modifications by Dr. Ramzan Virani pptx.pdf
byDr. Ramzan Virani
 
PPTX
Unit 3- Culture.pptx....................
byAkanksha Kotangale
 
PDF
Risks and opportunities of artificial intelligence in education: A critical view
byYannis
 
PPTX
" Jaya : Silence as Resistance " - That long silence
bydharabhandari35
 
PPTX
bundle of care.pptx Priti Bala @ BRD med
bypritibala13
 
PPTX
Poster Based Ethical Reflection - Dharma and Values Poster.pptx
byRajshreeBeneymadoo
 
PDF
Aminoglycosides.pdf for B.Pharmacy Medicinal Chemistry-III (BP601T), GPAT, a...
bymominzarinamdnajeeb
 
PDF
VIVA or SHORT ANSWER QUESTIONS or 2 MARKS QUESTIONS CHILD HEALTH NURSING.pdf
byPRADEEP ABOTHU
 
PPTX
Setting Up and Processing Down Payments in Odoo 18 Sales
byCeline George
 
PPTX
YSPH VMOC Special Report - Measles - The Americas 1-25-2026
byYale School of Public Health - The Virtual Medical Operations Center (VMOC)
 
Alma Šuto - From Tradition to Innovation: Creative AI in Education
bybvtricks
 
Take This Quirky Quiz! - QGI 1st Anniversary .pdf
byNiyati Jois
 
Fruit Fermentation_ Ethanol & Sugar Estimation- Dr. Shikha Gaikwad
byinsighteduwithme
 
Infrared Spectroscopy (IR spectroscopy).ppt
byLife sciences
 
Central Line Associated Bloodstream Infection
bynabinabhaila40
 
Oscillations /Revision notes prepared by K sandeep swamy (Msc,BEd)/For online...
bySandeep Swamy
 
Statistical Data Analysis using R Programming.pptx
byVETRISELVIP1
 
ĐỀ MINH HỌA KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2026 MÔN TIẾNG ANH 2026...
byNguyen Thanh Tu Collection
 
Day 2 ppt english.powerpoint presentation ppt
byJeahMaeMedez
 
NMR Spectroscopy: Principles and Applications
byVanitha Rajakumar
 
Beak Modifications by Dr. Ramzan Virani pptx.pdf
byDr. Ramzan Virani
 
Unit 3- Culture.pptx....................
byAkanksha Kotangale
 
Risks and opportunities of artificial intelligence in education: A critical view
byYannis
 
" Jaya : Silence as Resistance " - That long silence
bydharabhandari35
 
bundle of care.pptx Priti Bala @ BRD med
bypritibala13
 
Poster Based Ethical Reflection - Dharma and Values Poster.pptx
byRajshreeBeneymadoo
 
Aminoglycosides.pdf for B.Pharmacy Medicinal Chemistry-III (BP601T), GPAT, a...
bymominzarinamdnajeeb
 
VIVA or SHORT ANSWER QUESTIONS or 2 MARKS QUESTIONS CHILD HEALTH NURSING.pdf
byPRADEEP ABOTHU
 
Setting Up and Processing Down Payments in Odoo 18 Sales
byCeline George
 
YSPH VMOC Special Report - Measles - The Americas 1-25-2026
byYale School of Public Health - The Virtual Medical Operations Center (VMOC)
 

Deep Learning Tutorial | Deep Learning TensorFlow | Deep Learning With Neural Networks | Simplilearn

  • 2.
    Geolocation with NeuralNetwork How does a neural network recognize the location of an image? Artificial Neural Network New image of a placeImages of millions of places Identifies the place
  • 3.
    Geolocation with NeuralNetwork Pixels of millions of images Feed to Neural Network Recognizes landmarks, landscapes, architectural styles, road signs, etc New image of a place Identifies the place How does a neural network recognize the location of an image?
  • 4.
    What’s in itfor you? Types of Neural Networks Applications of Deep Learning Working of Neural Network Introduction to TensorFlow Use case implementation using TensorFlow What is Deep Learning? What is a Neural Network? Implementing Logic Gates using Perceptron What is a Perceptron? Why do we need Deep Learning?
  • 5.
    What is DeepLearning?
  • 6.
    What is DeepLearning? Deep Learning is a subset of Machine Learning that has networks which are capable of learning from data that is unstructured or unlabeled and works similar to the functioning of a human brain. Artificial Intelligence Machine Learning Deep Learning Ability of a machine to imitate intelligent human behavior Application of AI that allows a system to automatically learn and improve from experience Application of Machine Learning that uses complex algorithms and deep neural nets to train a model
  • 7.
    Why do weneed Deep Learning? Machine Learning works only with large sets of structured data, while Deep Learning can work with both structured and unstructured data Deep Learning algorithms can perform complex operations easily while Machine Learning Algorithms cannot Machine Learning algorithms use labelled sample data to extract patterns, while Deep Learning accepts large volumes of data as input, analyze the input to extract features out of an object Performance of Machine Learning algorithms decreases as the amount of data increase, so to maintain the performance of the model we need Deep Learning Works with unstructured data Handle complex operations Feature Extraction Achieve best performance
  • 8.
    What is aNeural Network?
  • 9.
    What is aNeural Network? Neuron X1 X2 Xn Y Output w1 w2 w n Input 1 Input 2 Input n Neural Networks are modeled after biological neural networks that allow computers to learn and interact like humans do. It has interconnected neurons with dendrites that receive inputs, and based on those inputs, it produces an electric signal i.e. output through the axon. Biological Neuron
  • 10.
    What is aNeural Network? Neuron X1 X2 Xn Y Output w1 w2 w n Input 1 Input 2 Input n Neural Network has interconnected neurons that receive some inputs, processes those inputs in layers to produce the output. Artificial Neuron
  • 11.
    Biological Neurons VsArtificial Neuron Dendrites -------> Inputs Neuron X1 X2 Xn Y Output w1 w2 w n Dendrites Input 1 Input 2 Input n Inputs
  • 12.
    Biological Neurons VsArtificial Neuron Cell Nucleus Neuron Input 1 Input 2 Input n Y Output w1 w2 w n Nodes X1 X2 Xn Cell Nucleus -------> Nodes
  • 13.
    X1 X2 Xn Biological Neurons VsArtificial Neuron Synapse Neuron Input 1 Input 2 Input n Y Output Weights w1 w2 wn Synapse -------> Weights
  • 14.
    Biological Neurons VsArtificial Neuron X1 X2 Xn Neuron Input 1 Input 2 Input n w1 w2 wn Axon Axon -------> Output Y Output
  • 15.
    What is aPerceptron?
  • 16.
    What is aPerceptron? A Perceptron is the basic part of a neural network. It represents a single neuron of a human brain and is used for binary classifiers. X1 X2 Xn Input 1 Input 2 Input n w1 w2 wn Y Output Net Input Function Activation Function ERROR
  • 17.
    Perceptron Learning Rule w X1 X2 Xn Input1 Input 2 Input n w2 Y Output Activation Function ERROR w1 n Net Input Function Inputs are multiplied with the weights and a summation is performed, plus a bias is added Bias i=1 n w x + b i i* Step 1
  • 18.
    Perceptron Learning Rule w X1 X2 Xn Input1 Input 2 Input n w2 Y Output Activation Function ERROR w1 n Net Input Function The weighted sum of inputs is passed to an activation function to determine if a neuron will fire or not Step 2
  • 19.
    Perceptron Learning Rule w X1 X2 Xn Input1 Input 2 Input n w2 Y Output Activation Function ERROR w1 n Net Input Function Perceptron receives input signals and if the sum of the input signals exceeds a certain threshold value, it either outputs a signal or does not return an output Output = 0, if i=1 n w x + b < threshold i i* 1, if i=1 n w x + b >= thresholdi i* Step 3
  • 20.
    Perceptron Learning Rule w X1 X2 Xn Input1 Input 2 Input n w2 Y Output Activation Function ERROR w1 n Net Input Function The error in the output is backpropagated and weights are updated to minimize the error Step 4
  • 21.
    Perceptron Learning Rule w X1 X2 Xn Input1 Input 2 Input n w2 Y Output Activation Function ERROR w1 n Net Input Function Repeat steps 1 to 4 in order to generate the desired output
  • 22.
    Implementing Logic Gatesusing Perceptron In 1943, neuroscientist Warren McCulloch and logician Walter Pitts published a paper showing how neurons could implement the three logical functions (AND, OR, XOR). The neurons they used were simple threshold neurons which they named it Perceptron. Warren McCulloch Walter Pitts
  • 23.
    Implementing Logic Gatesusing Perceptron A logic gate is the basic building block of a digital circuit. Most logic gates have 2 inputs and 1 output. At any given moment, every terminal is in one of the two binary conditions low (0) or high (1), represented by different voltage levels. Popular Logic Gates AND OR NAND NOR NOT XOR
  • 24.
    Implementing AND Gate Usingthe Logic Gates, Neural Networks can learn on their own without having to manually code the logic Input (A) Input (B) Output 0 0 0 0 1 0 1 0 0 1 1 1 AND The output of Perceptron is true or positive if both the inputs are true, else false
  • 25.
    Implementing AND Gate Aand B are input neurons. The red neuron is our output neuron. The threshold value is 1. If the sum of the weighted input neurons is greater than the threshold, the output is 1 else 0. Input (A) Input (B) Output 0.7*0 0.7*0 0 0.7*0 0.7*1 0.7 0.7*1 0.7*0 0.7 0.7*1 0.7*1 1.4 A B 0.7 0.7 = 1 This exceeds the threshold, so output is 1 We have designed a neuron which implements a logical AND gate w x1 1* w x 2 2* w x +1 1* w x 2 2*
  • 26.
    Implementing OR Gate Usingthe Logic Gates, Neural Networks can learn on their own without having to manually code the logic Input (A) Input (B) Output 0 0 0 0 1 1 1 0 1 1 1 1 OR The output of Perceptron is true or positive if either of the inputs are true, else false
  • 27.
    Implementing OR Gate Aand B are input neurons. The red neuron is our output neuron. The threshold value is 1. If the sum of the weighted input neurons is greater than the threshold, the output is 1 else 0. Input (A) Input (B) Output 1.2*0 1.2*0 0 1.2*0 1.2*1 1.2 1.2*1 1.2*0 1.2 1.2*1 1.2*1 2.4 A B 1.2 1.2 = 1 These exceed the threshold, so output is 1 w x1 1* w x 2 2* w x +1 1* w x 2 2* We have designed a neuron which implements a logical OR gate
  • 28.
    Implementing XOR Gate Usingthe Logic Gates, Neural Networks can learn on their own without having to manually code the logic Input (A) Input (B) Output 0 0 0 0 1 1 1 0 1 1 1 0 XOR The output of Perceptron is true or positive if one of the inputs is true, else false
  • 29.
    Implementing XOR Gate XORgate requires an intermediate hidden layer to achieve the logic of a XOR gate XOR Implementation 5 X X h h O 1 2 3 4 w13 w14 w23 w24 w45 w35 5 • X1 and X2 are inputs and h3 and h4 are the hidden layers. B3, B4 and B5 are the biases for h3, h4 and O5. • h3 = sigmoid (X1*w13 + X2*w23 – B3) • h4 = sigmoid (X2*w14 + X2*w24 – B4) • O5 = sigmoid (h3*w35 + h4*w45 – B5)
  • 30.
    Implementing XOR Gate XORgate requires an intermediate hidden layer to achieve the logic of a XOR gate 5 X X h h O 1 2 3 4 20 -20 20 -20 20 20 5 Sigmoid(20*0+20*0-10) 0 Sigmoid(20*1+20*1-10) 1 Sigmoid(20*0+20*1-10) 1 Sigmoid(20*1+20*0-10) 1 ~~ ~~ ~~ ~~ Sigmoid(-20*0-20*0+30) 1 Sigmoid(-20*1-20*1+30) 0 Sigmoid(-20*0-20*1+30) 1 Sigmoid(-20*1-20*0+30) 1 ~~ ~~ ~~ ~~ b= -10 Sigmoid(20*0+20*1-30) 0 Sigmoid(20*1+20*0-30) 0 Sigmoid(20*1+20*1-30) 1 Sigmoid(20*1+20*1-30) 1 ~~ ~~ ~~ ~~ h3 h4 Output These exceed the threshold, so output is 1 b= 30 b= -30 = 1 = 1 = 1
  • 31.
  • 32.
    Types of NeuralNetworks Pattern Recognition ANN CNN RNN DNN DBN Image Processing Acoustic Modeling Recursive Neural Network Cancer Detection Neural Networks are mainly classified into 5 types Artificial Neural Network Convolution Neural Network Speech Recognition Deep Neural Network Deep Belief Network
  • 33.
  • 34.
    Applications of DeepLearning Deep Learning allows us to build machines that can play games Playing Games
  • 35.
    Applications of DeepLearning Composing Music Deep Neural Nets can be used to produce music by making computers learn the patterns in a composition
  • 36.
    Applications of DeepLearning Autonomous Driving Cars Distinguishes different types of objects, people, road signs and drives without human intervention
  • 37.
    Applications of DeepLearning Building Robots Deep Learning is used to train robots to perform human tasks
  • 38.
    Applications of DeepLearning Medical Diagnosis Deep Neural Nets are used to identify suspicious lesions and nodules in lung cancer patients
  • 39.
  • 40.
    Working of NeuralNetwork Let’s find out how an Artificial Neural Network can be used to identify different shapes like Squares, Circles and Triangles How to identify various shapes using a neural network? Feed the shapes to a neural network as input Artificial Neural Network
  • 41.
    Working of NeuralNetwork Artificial Neural Network 28 28 Strengths 28 28 = 784* • 28*28 pixels of the input image is taken as input i.e. 784 neurons Lets consider the shape of a square Shape of a Square
  • 42.
    Working of NeuralNetwork 28 28 Strengths • 28*28 pixels of the input image is taken as input i.e. 784 neurons 28 28 = 784* 0.78 Activation • Each neuron holds a number called Activation that represents grayscale value of the corresponding pixel ranging from 0 to 1. 1 for white pixel and 0 for black pixel Lets consider the shape of a square Artificial Neural Network
  • 43.
    Working of NeuralNetwork Lets consider the shape of a square 28 28 Strengths • 28*28 pixels of the input image is taken as input i.e. 784 neurons • Each neuron is lit up when its activation is close to 1 28 28 = 784* • Each neuron holds a number called Activation that represents grayscale value of the corresponding pixel ranging from 0 to 1. 1 for white pixel and 0 for black pixel Artificial Neural Network
  • 44.
  • 45.
  • 46.
  • 47.
    Working of NeuralNetwork X1 X2 Xn w1 w2 wn Step 1 i=1 n w x + b i i* Activation Function Step 2 i=1 n w x + b ii*( ) Lets find out how an Artificial Neural Network can be used to identify different shapes Identifies different shapes Squares Circles Triangles Pixels of images fed as input
  • 48.
    Working of NeuralNetwork Lets find out how an Artificial Neural Network can be used to identify different shapes X1 X2 Xn Y W1 W2 W3 . . . . . . . . . Wn W22 W23 W33 . . . . . . . . . Wn2 W11 W21 W31 . . . . . . . . . Wn1 Apply the weights Identifies different shapes Squares Circles Triangles^ Pixels of images fed as input
  • 49.
    Working of NeuralNetwork Lets find out how an Artificial Neural Network can be used to identify different shapes X1 X2 Xn Y^ Apply the activation functions Identifies different shapes Squares Circles Triangles
  • 50.
    Working of NeuralNetwork Lets find out how an Artificial Neural Network can be used to identify different shapes X1 X2 Xn Y^ Compare it with actual output Predicted Output Actual Output Y
  • 51.
    Working of NeuralNetwork Applying the cost function to minimize the difference between predicted and actual output using gradient descent algorithm Predicted Output X1 X2 Xn Y^ Actual Output Compare it with actual output Y Cost Function: C = ½( Y – Y ) 2
  • 52.
    Working of NeuralNetwork Neural Networks use Backpropagation method along with improve the performance of the Neural Net. A cost function is used to reduce the error rate between predicted and actual output. X X X Y^ Cost Function: C = ½( Y – Y ) 2 1 2 n Y
  • 53.
    Cost Function The Costvalue is the difference between the neural nets predicted output and the actual output from a set of labelled training data. The least cost value is obtained by making adjustments to the weights and biases iteratively throughout the training process. X X Xn Y Y^ W1 W2 W3 . . . . . . . . . Wn W22 W23 W33 . . . . . . . . . Wn2 W11 W21 W31 . . . . . . . . . Wn1 1 2 Cost Function: C = ½( Y – Y ) 2
  • 54.
    Gradient Descent Slower Faster Theperson will take more time to reach the base of the mountain if the slope is gentle and will come down faster if the slope is steep. Likewise, a Neural Net will train slowly if the Gradient is small and it will train quickly if the Gradient is large. Gradient Descent is an optimization algorithm for finding the minimum of a function A person trying to reach the base of a mountain
  • 55.
    Gradient Descent Gradient Descentis an optimization algorithm for finding the minimum of a functionGradient Descent is an optimization algorithm for finding the minimum of a function C = ½( Y – Y )^ 2 C W C W Best Gradient Global Minimum cost Initial Weight
  • 56.
    Stochastic Gradient Descent C W Best LocalMinimum Global Minimum It does not require the cost function to be convex Takes the rows one by one, runs the neural network and then adjusts the weights Helps you avoid the local minimum as it performs 1 iteration at a time
  • 57.
    Deep Learning Platforms Torch Keras 4main platforms TensorFlow DeepLearning4J (java)
  • 58.
  • 59.
    Introduction to TensorFlow •TensorFlow is a Deep Learning tool to define and run computations involving tensors. • A tensor is a generalization of vectors and matrices to potentially higher dimensions. • The array of data passed in each layer of nodes is known as Tensor. a m k q d 2 4 8 1 1 9 3 2 5 4 4 6 6 3 3 7 8 2 9 5 Tensor of Dimensions[5] Tensor of Dimensions[5,4]Tensor of Dimension[3,3,3]
  • 60.
    Introduction to TensorFlow •TensorFlow is a Deep Learning tool to define and run computations involving tensors. • A tensor is a generalization of vectors and matrices to potentially higher dimensions. • The array of data passed in each layer of nodes is known as Tensor. 1.2 3.5 2.2… 4.7 10 4.5… 2.2 7.8 8.1… 3.6 2.5 4.5… Arrays of data with different dimensions and ranks go as input to the network
  • 61.
  • 62.
    Introduction to TensorFlow Opensource software library developed by Google Most popular library in Deep Learning Can run on either CPU or GPU Can create data flow graphs that have nodes and edges Used for Machine Learning applications such as Neural Networks
  • 63.
    Use case Implementationusing TensorFlow Lets build a neural network to identify hand written digits using MNIST Database. Hand written digits from MNIST Database Modified National Institute of Standards and Technology Database Has a collection of 70,000 handwritten digits Digit labels identify each of the digits from 0 to 9
  • 64.
    Use case Implementationusing TensorFlow Lets build a neural network to identify hand written digits using MNIST Database. Hand written digits from MNIST Database Pixels of digits fed as input to the network New image of a digit Identifies the digit That’s digit 3
  • 65.
    Softmax Function ……………. 0 12 9 28*28=784 pixels ……………. Softmax (Ln) = Ln e e L
  • 66.
    Use case Implementationusing TensorFlow 1. Import MNIST Data using TensorFlow 2. Check the type of Dataset
  • 67.
    Use case Implementationusing TensorFlow 3. Array of Training images 4. Number of images for Training, Testing and Validation
  • 68.
    Use case Implementationusing TensorFlow 5. Visualizing the Data
  • 69.
    Use case Implementationusing TensorFlow 6. Maximum and minimum value of the pixels in the image
  • 70.
    Use case Implementationusing TensorFlow 7. Create the Model
  • 71.
    Use case Implementationusing TensorFlow 8. Create the Session 9. Evaluate the Trained model on Test data

Editor's Notes