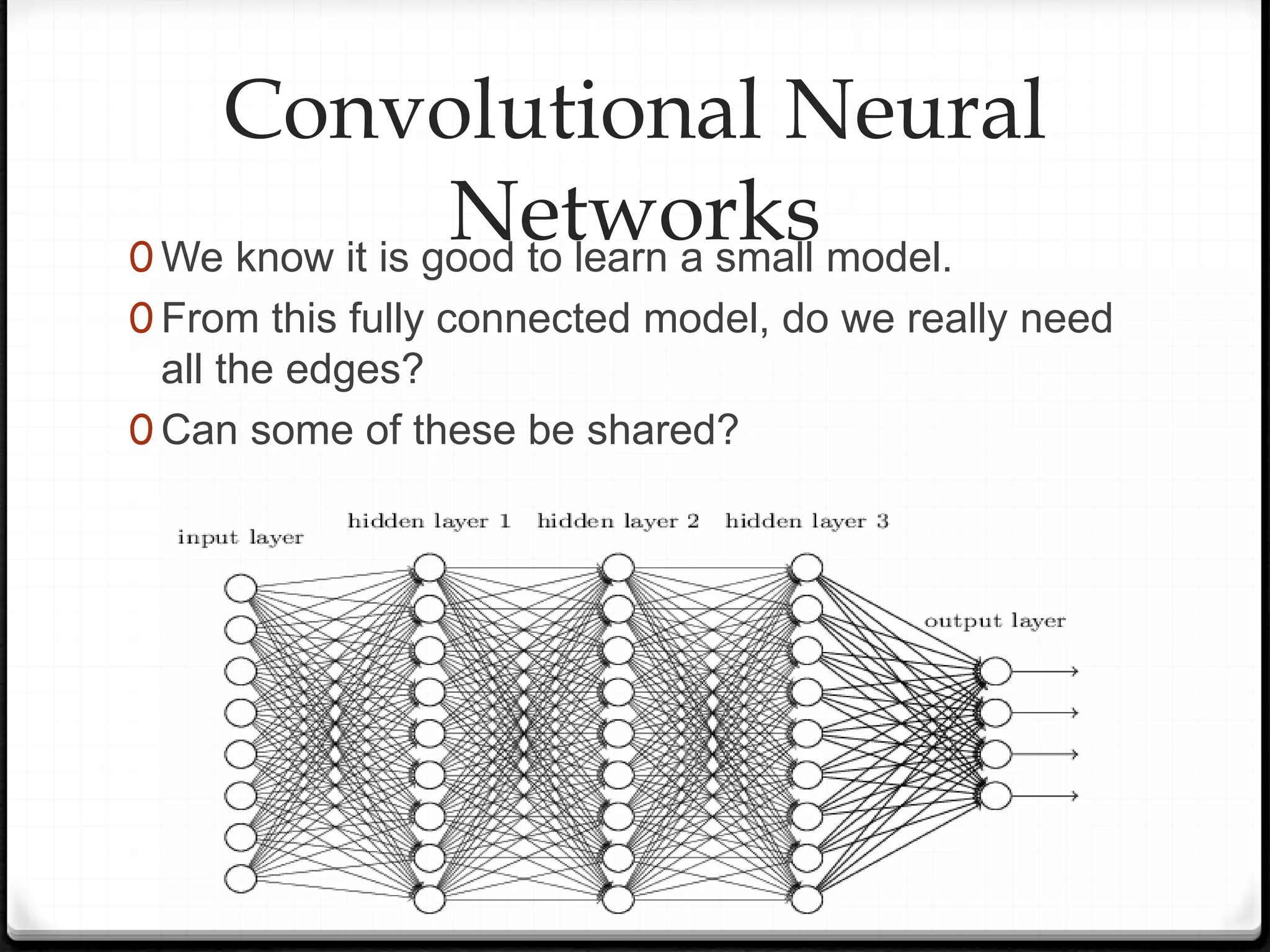
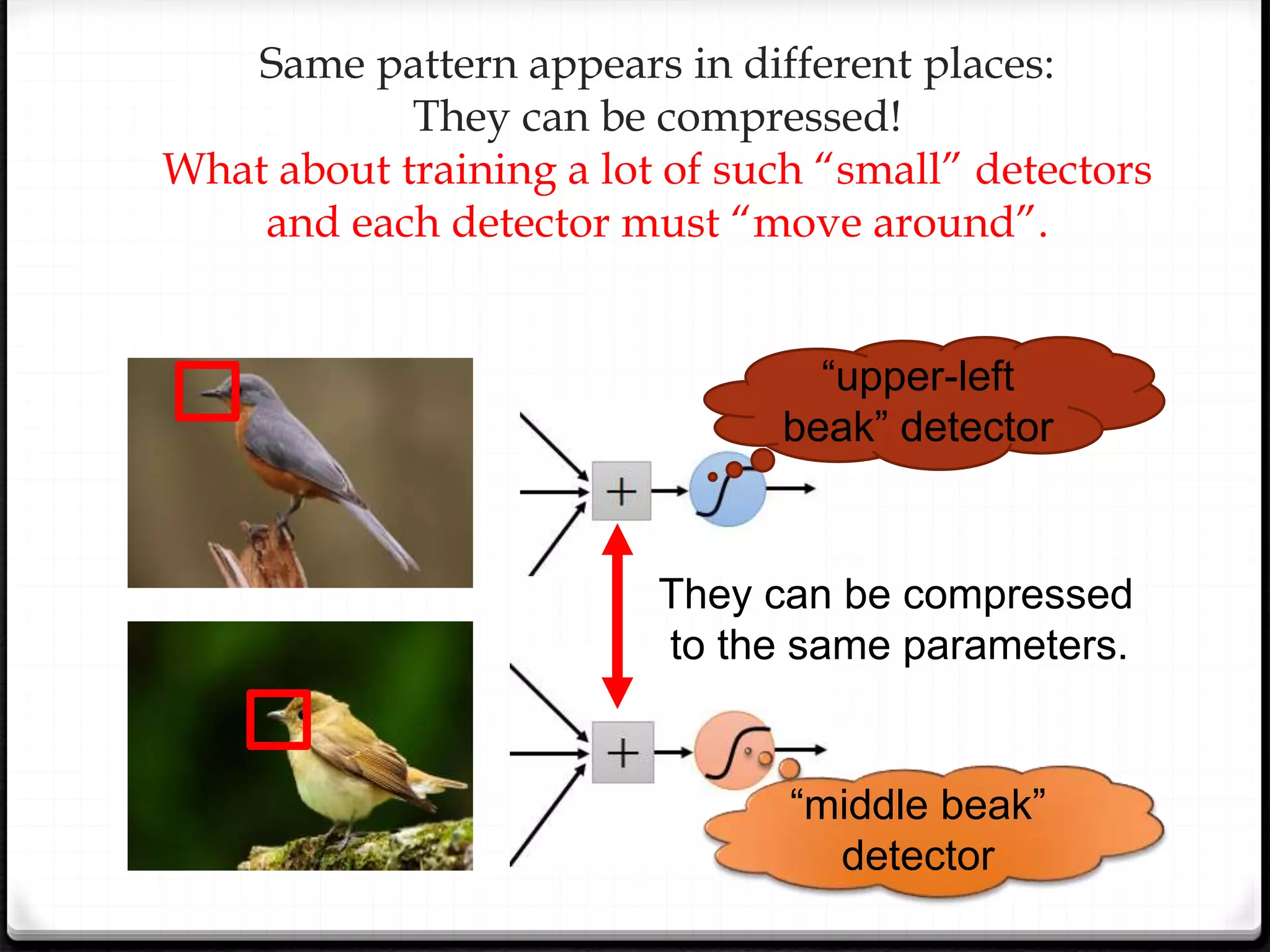
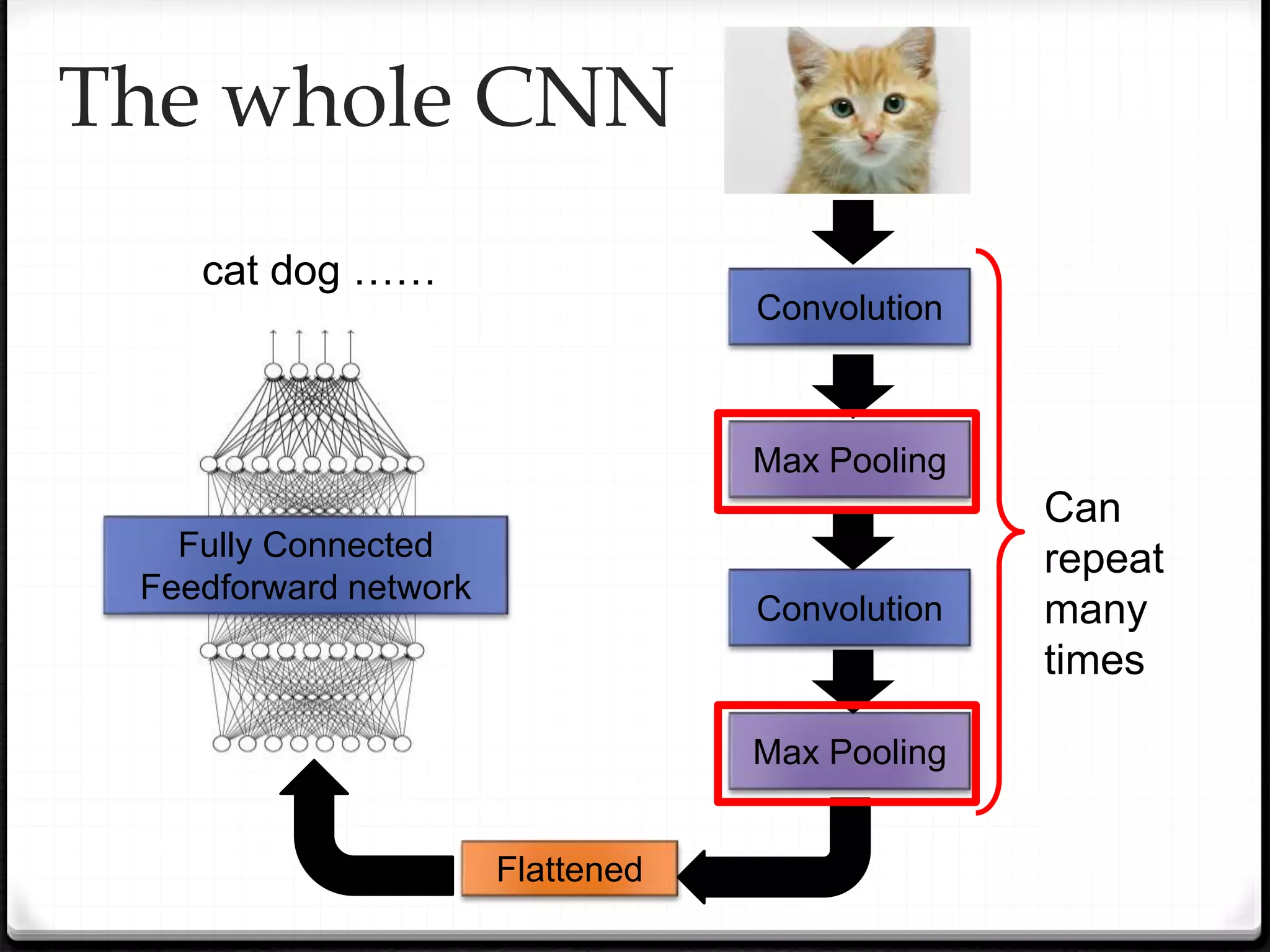
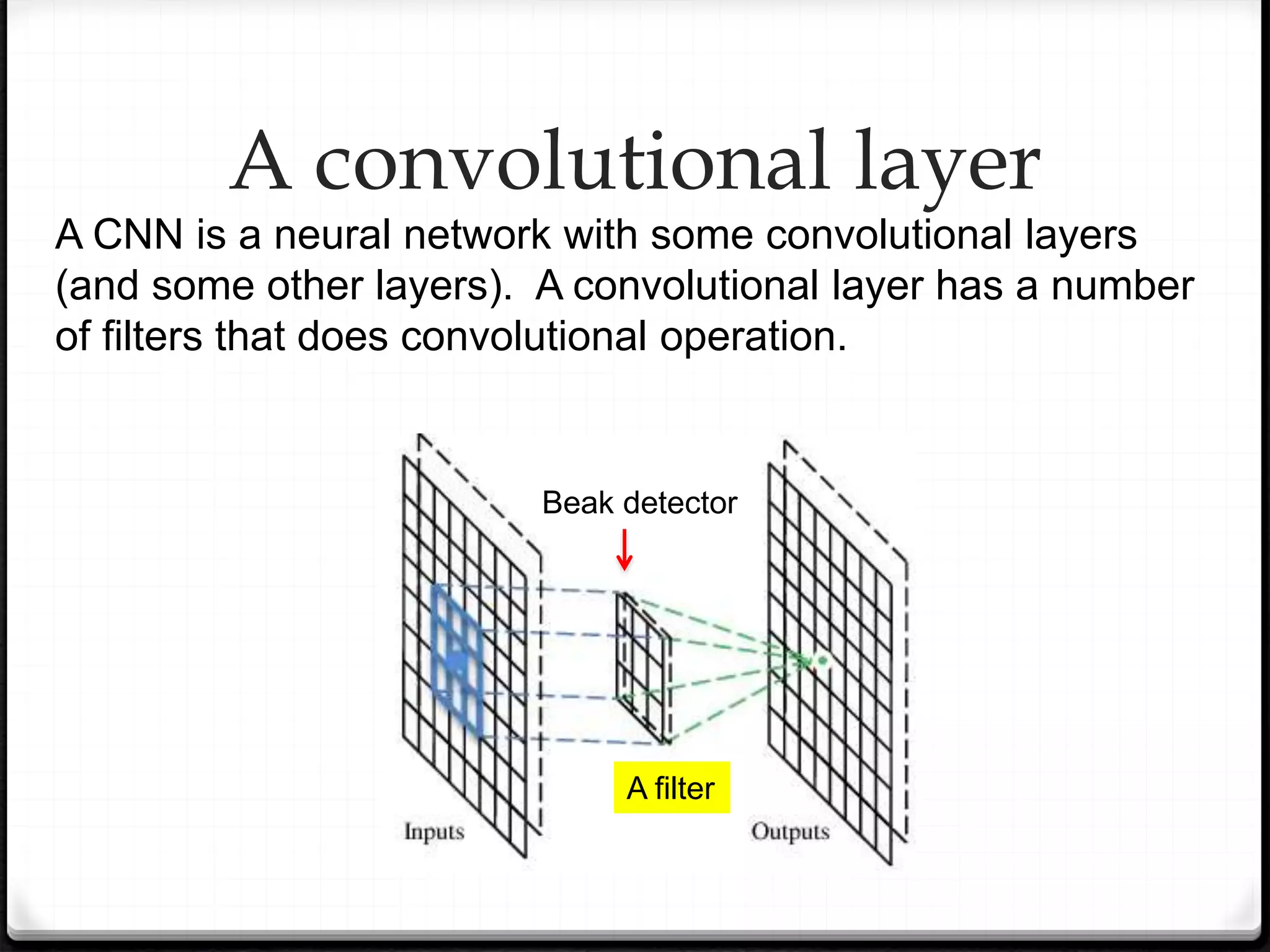
This document provides an overview of machine learning and deep learning concepts. It begins with an introduction to machine learning basics, including supervised and unsupervised learning. It then discusses deep learning, why it is useful, and its main components like activation functions, optimizers, and regularization methods. The document explains deep neural network architecture including convolutional neural networks. It provides examples of convolutional and max pooling layers and how they help reduce parameters in neural networks.

2. Outline
 Machine Learning basics
 Introduction to Deep Learning
 what is Deep Learning
 why is it useful
 Main components/hyper-parameters:
 activation functions
 optimizers, cost functions and training
 regularization methods
 tuning
 classification vs. regression tasks
 DNN basic architecture:
 Convolutional neural network
Most material from CS224 NLP with DL course at Stanford

3. Machine learning is a field of computer science that gives computers the
ability to learn without being explicitly programmed
Methods that can learn from and make predictions on data
Labeled Data
Labeled Data
Machine Learning
algorithm
Learned model Prediction
Training
Prediction
Machine Learning Basics

4. Regression
Supervised: Learning with a labeled training set
Example: email classification with already labeled emails
Unsupervised: Discover patterns in unlabeled data
Example: cluster similar documents based on text
Reinforcement learning: learn to act based on feedback/reward
Example: learn to play Go, reward: win or lose
Types of Learning
class A
class A
Classification Clustering
http://mbjoseph.github.io/2013/11/27/measure.html

5. Most machine learning methods work well because of human-designed
representations and input features
ML becomes just optimizing weights to best make a final prediction
ML vs. Deep Learning

6. Deep learning algorithms attempt to learn (multiple levels of) representation by
using a hierarchy of multiple layers
If you provide the system tons of information, it begins to understand it and
respond in useful ways.
What is Deep Learning (DL) ?
https://www.xenonstack.com/blog/static/public/uploads/media/machine-learning-vs-deep-learning.png

7. o Manually designed features are often over-specified, incomplete and take a
long time to design and validate
o Learned Features are easy to adapt, fast to learn
o Deep learning provides a very flexible, (almost?) universal, learnable
framework for representing world, visual and linguistic information.
o Can learn both unsupervised and supervised
o Effective end-to-end joint system learning
o Utilize large amounts of training data
Why is DL useful?
In ~2010 DL started outperforming
other ML techniques
first in speech and vision, then NLP

8. Neural Network Intro
Demo
How do we train?
𝒉 = 𝝈(𝐖𝟏𝒙 + 𝒃𝟏)
𝒚 = 𝝈(𝑾𝟐𝒉 + 𝒃𝟐)
𝒉
𝒚
𝒙
4 + 2 = 6 neurons (not counting inputs)
[3 x 4] + [4 x 2] = 20 weights
4 + 2 = 6 biases
26 learnable parameters
Weights
Activation functions

9. Training
Sample
labeled data
(batch)
Forward it
through the
network, get
predictions
Back-
propagate
the errors
Update the
network
weights
Optimize (min. or max.) objective/cost function 𝑱(𝜽)
Generate error signal that measures difference
between predictions and target values
Use error signal to change the weights and get more
accurate predictions
Subtracting a fraction of the gradient moves you
towards the (local) minimum of the cost function
https://medium.com/@ramrajchandradevan/the-evolution-of-gradient-descend-optimization-algorithm-4106a6702d39

10. Non-linearities needed to learn complex (non-linear) representations of data,
otherwise the NN would be just a linear function
More layers and neurons can approximate more complex functions
Activation functions
W1W2𝑥 = 𝑊𝑥
Full list: https://en.wikipedia.org/wiki/Activation_function
http://cs231n.github.io/assets/nn1/layer_sizes.jpeg

11. Activation: Sigmoid
+ Nice interpretation as the firing rate of a neuron
• 0 = not firing at all
• 1 = fully firing
- Sigmoid neurons saturate and kill gradients, thus NN will barely learn
• when the neuron’s activation are 0 or 1 (saturate)
� gradient at these regions almost zero
� almost no signal will flow to its weights
� if initial weights are too large then most neurons would saturate
Takes a real-valued number and
“squashes” it into range between 0
and 1.
𝑅𝑛 → 0,1
http://adilmoujahid.com/images/activation.png

12. Activation: ReLU
Takes a real-valued number and
thresholds it at zero
𝑅𝑛 → 𝑅+
𝑛
Most Deep Networks use ReLU nowadays
� Trains much faster
• accelerates the convergence of SGD
• due to linear, non-saturating form
� Less expensive operations
• compared to sigmoid/tanh (exponentials etc.)
• implemented by simply thresholding a matrix at zero
� More expressive
� Prevents the gradient vanishing problem
f 𝑥 = max(0, 𝑥)
http://adilmoujahid.com/images/activation.png

13. Overfitting
Learned hypothesis may fit the
training data very well, even
outliers (noise) but fail to
generalize to new examples (test
data)
http://wiki.bethanycrane.com/overfitting-of-data
https://www.neuraldesigner.com/images/learning/selection_error.svg

14. L2 = weight decay
• Regularization term that penalizes big weights, added to
the objective
• Weight decay value determines how dominant regularization is
during gradient computation
• Big weight decay coefficient  big penalty for big weights
Regularization
Dropout
• Randomly drop units (along with their
connections) during training
• Each unit retained with fixed probability p,
independent of other units
• Hyper-parameter p to be chosen (tuned)
𝐽𝑟𝑒𝑔 𝜃 = 𝐽 𝜃 + 𝜆
𝑘
𝜃𝑘
2
Early-stopping
• Use validation error to decide when to stop training
• Stop when monitored quantity has not improved after n subsequent epochs
• n is called patience
Srivastava, Nitish, et al. "Dropout: a simple way to prevent neural
networks from overfitting." Journal of machine learning research (2014)

15. Convolutional Neural
Networks
0 We know it is good to learn a small model.
0 From this fully connected model, do we really need
all the edges?
0 Can some of these be shared?

16. Consider learning an image:
0 Some patterns are much smaller than the whole
image
“beak” detector
Can represent a small region with fewer parameters

17. Same pattern appears in different places:
They can be compressed!
What about training a lot of such “small” detectors
and each detector must “move around”.
“upper-left
beak” detector
“middle beak”
detector
They can be compressed
to the same parameters.

18. The whole CNN
Fully Connected
Feedforward network
cat dog ……
Convolution
Max Pooling
Convolution
Max Pooling
Flattened
Can
repeat
many
times

19. A convolutional layer
A filter
A CNN is a neural network with some convolutional layers
(and some other layers). A convolutional layer has a number
of filters that does convolutional operation.
Beak detector

20. Convolution
1 0 0 0 0 1
0 1 0 0 1 0
0 0 1 1 0 0
1 0 0 0 1 0
0 1 0 0 1 0
0 0 1 0 1 0
6 x 6 image
3 -1 -3 -1
-3 1 0 -3
-3 -3 0 1
3 -2 -2 -1
-1 1 -1
-1 1 -1
-1 1 -1
Filter 2
-1 -1 -1 -1
-1 -1 -2 1
-1 -1 -2 1
-1 0 -4 3
Repeat this for each filter
stride=1
Two 4 x 4 images
Forming 2 x 4 x 4 matrix
Feature
Map

21. 1 0 0 0 0 1
0 1 0 0 1 0
0 0 1 1 0 0
1 0 0 0 1 0
0 1 0 0 1 0
0 0 1 0 1 0
image
convolution
-1 1 -1
-1 1 -1
-1 1 -1
1 -1 -1
-1 1 -1
-1 -1 1
1
x
2
x
…
…
36
x
…
…
1 0 0 0 0 1
0 1 0 0 1 0
0 0 1 1 0 0
1 0 0 0 1 0
0 1 0 0 1 0
0 0 1 0 1 0
Convolution v.s. Fully Connected
Fully-
connected

22. Max Pooling
3 -1 -3 -1
-3 1 0 -3
-3 -3 0 1
3 -2 -2 -1
-1 1 -1
-1 1 -1
-1 1 -1
Filter 2
-1 -1 -1 -1
-1 -1 -2 1
-1 -1 -2 1
-1 0 -4 3
1 -1 -1
-1 1 -1
-1 -1 1
Filter 1

23. Why Pooling
0Subsampling pixels will not change the
object
Subsampling
bird
bird
We can subsample the pixels to make image smaller
fewer parameters to characterize the image

24. A CNN compresses a fully
connected network in two
ways:
0 Reducing number of connections
0 Shared weights on the edges
0 Max pooling further reduces the complexity

25. The whole CNN
Convolution
Max Pooling
Convolution
Max Pooling
Can
repeat
many
times
A new image
The number of channels
is the number of filters
Smaller than the original
image
3 0
1
3
-1 1
3
0

26. The whole CNN
Fully Connected
Feedforward network
cat dog ……
Convolution
Max Pooling
Convolution
Max Pooling
Flattened
A new image
A new image

27. Flattening
3 0
1
3
-1 1
3
0 Flattened
3
0
1
3
-1
1
0
3
Fully Connected
Feedforward network

28. Only modified the network structure and
input format (vector -> 3-D tensor)
CNN in Keras
Convolution
Max Pooling
Convolution
Max Pooling
input
1 -1 -1
-1 1 -1
-1 -1 1
-1 1 -1
-1 1 -1
-1 1 -1
There are
25 3x3
filters.
…
…
Input_shape = ( 28 , 28 , 1)
1: black/white, 3: RGB
28 x 28 pixels
3 -1
-3 1
3

29. Only modified the network structure and
input format (vector -> 3-D array)
CNN in Keras
Convolution
Max Pooling
Convolution
Max Pooling
Input
1 x 28 x 28
25 x 26 x 26
25 x 13 x 13
50 x 11 x 11
50 x 5 x 5
How many parameters for
each filter?
How many parameters
for each filter?
9
225=
25x9

30. Only modified the network structure and
input format (vector -> 3-D array)
CNN in Keras
Convolution
Max Pooling
Convolution
Max Pooling
Input
1 x 28 x 28
25 x 26 x 26
25 x 13 x 13
50 x 11 x 11
50 x 5 x 5
Flattened
1250
Fully connected
feedforward network
Output

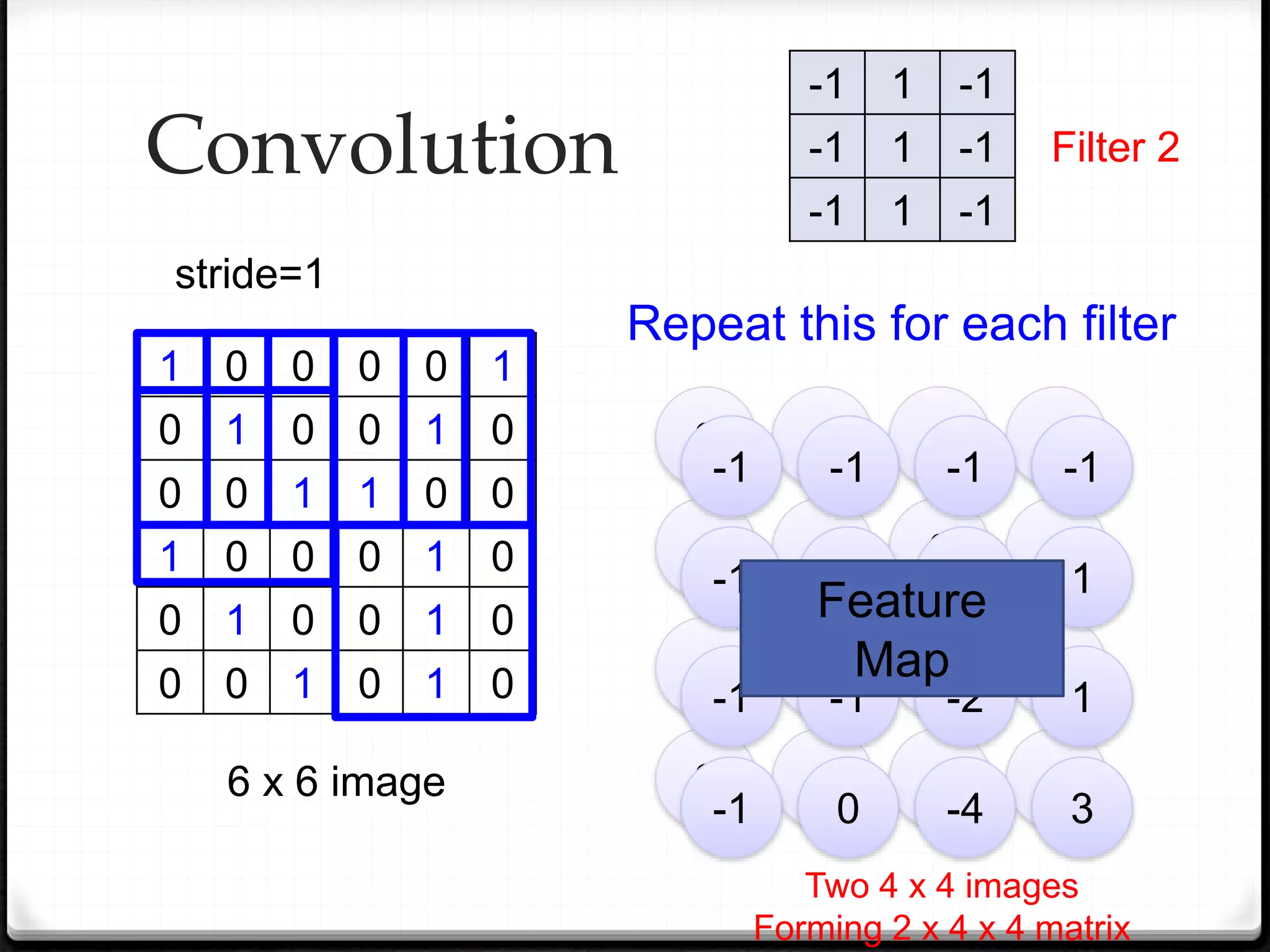
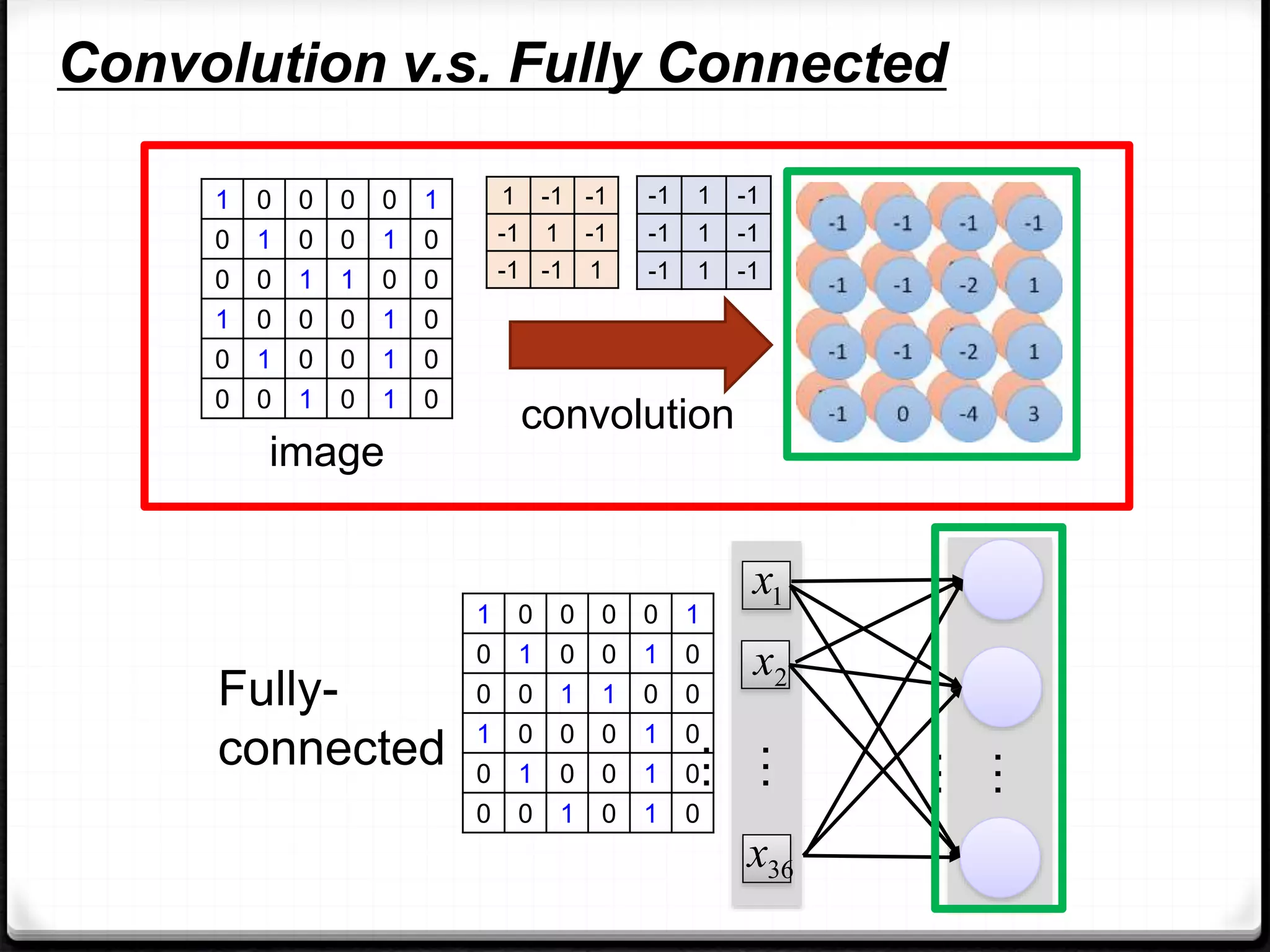
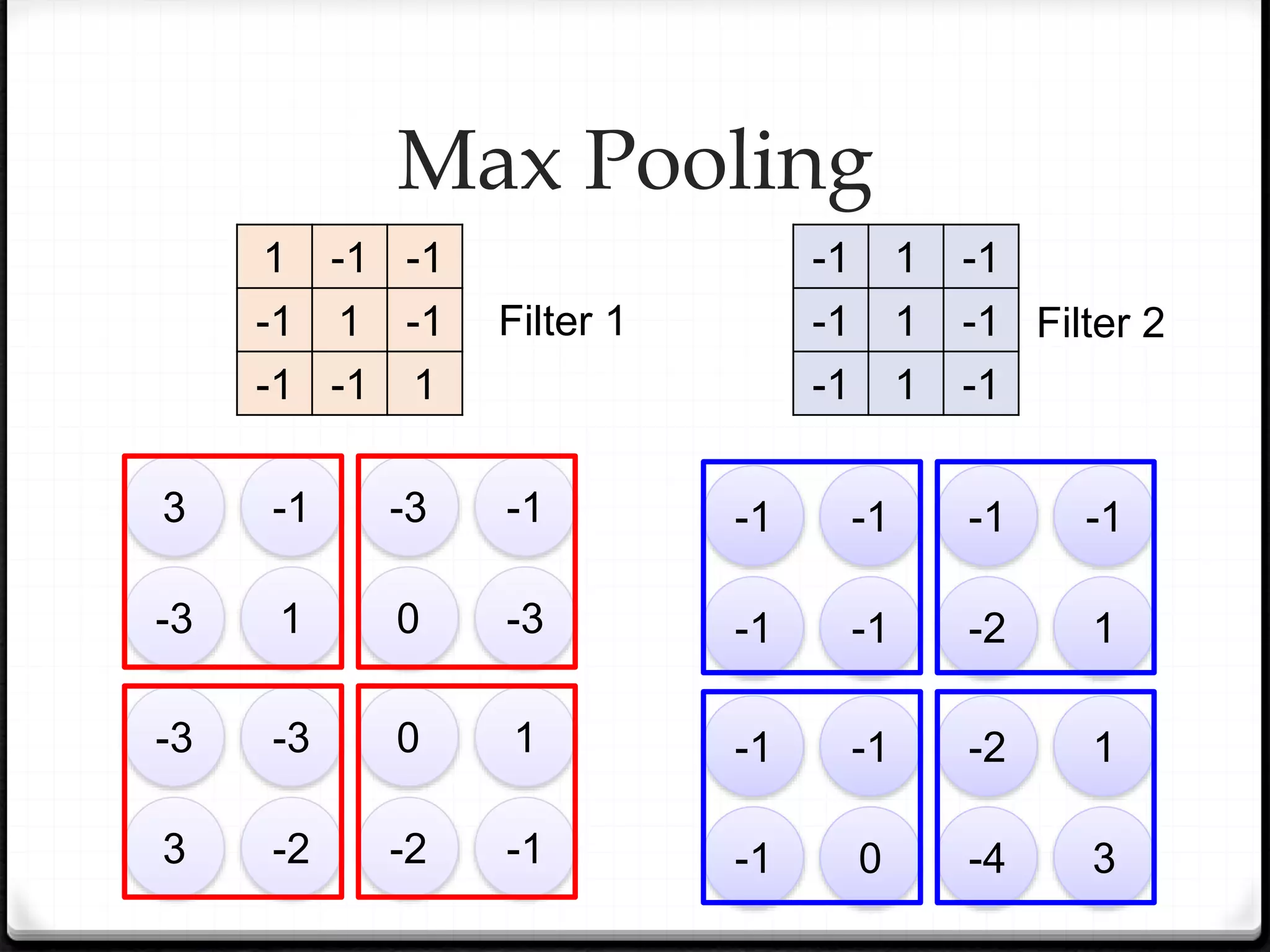
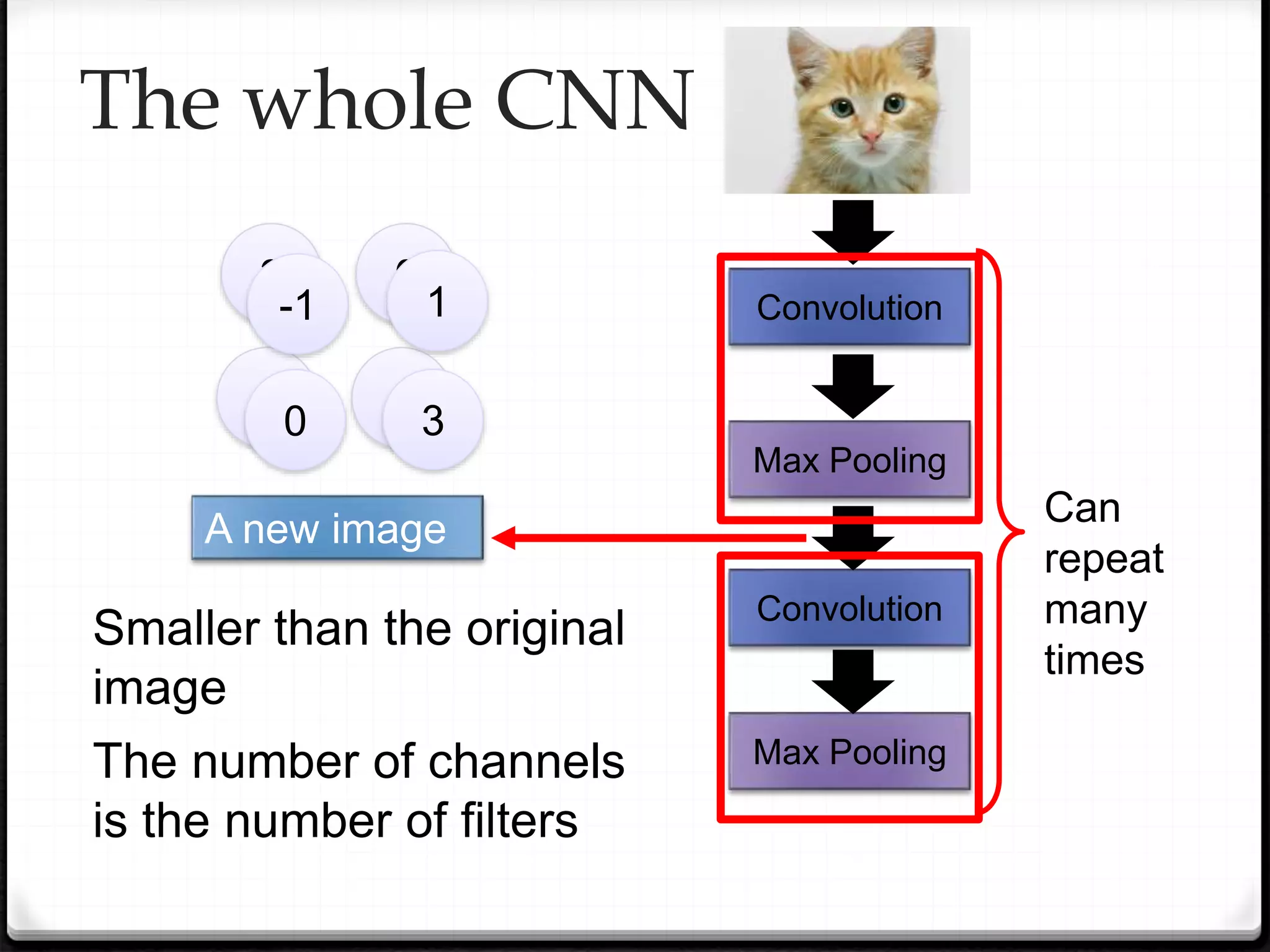
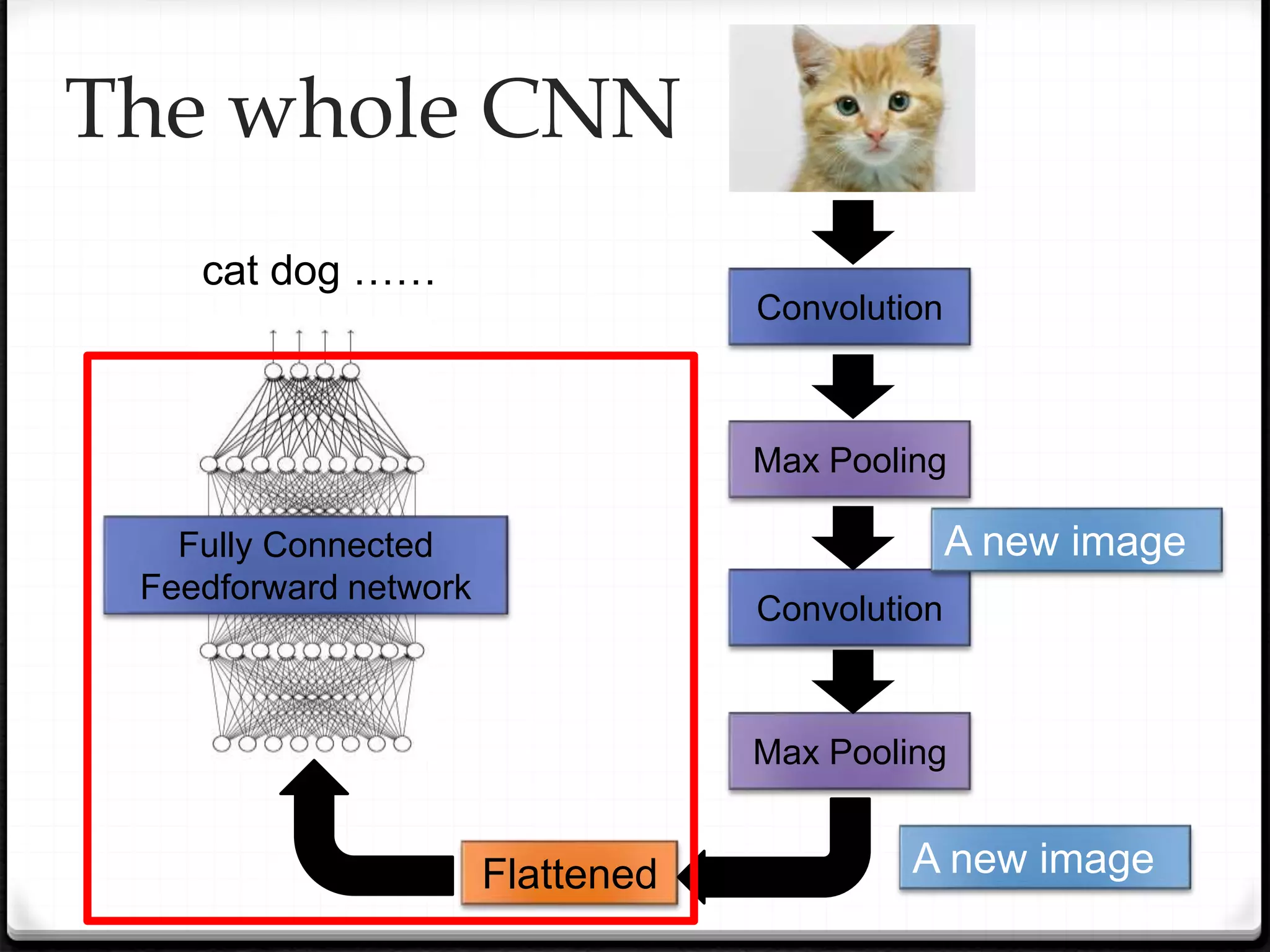
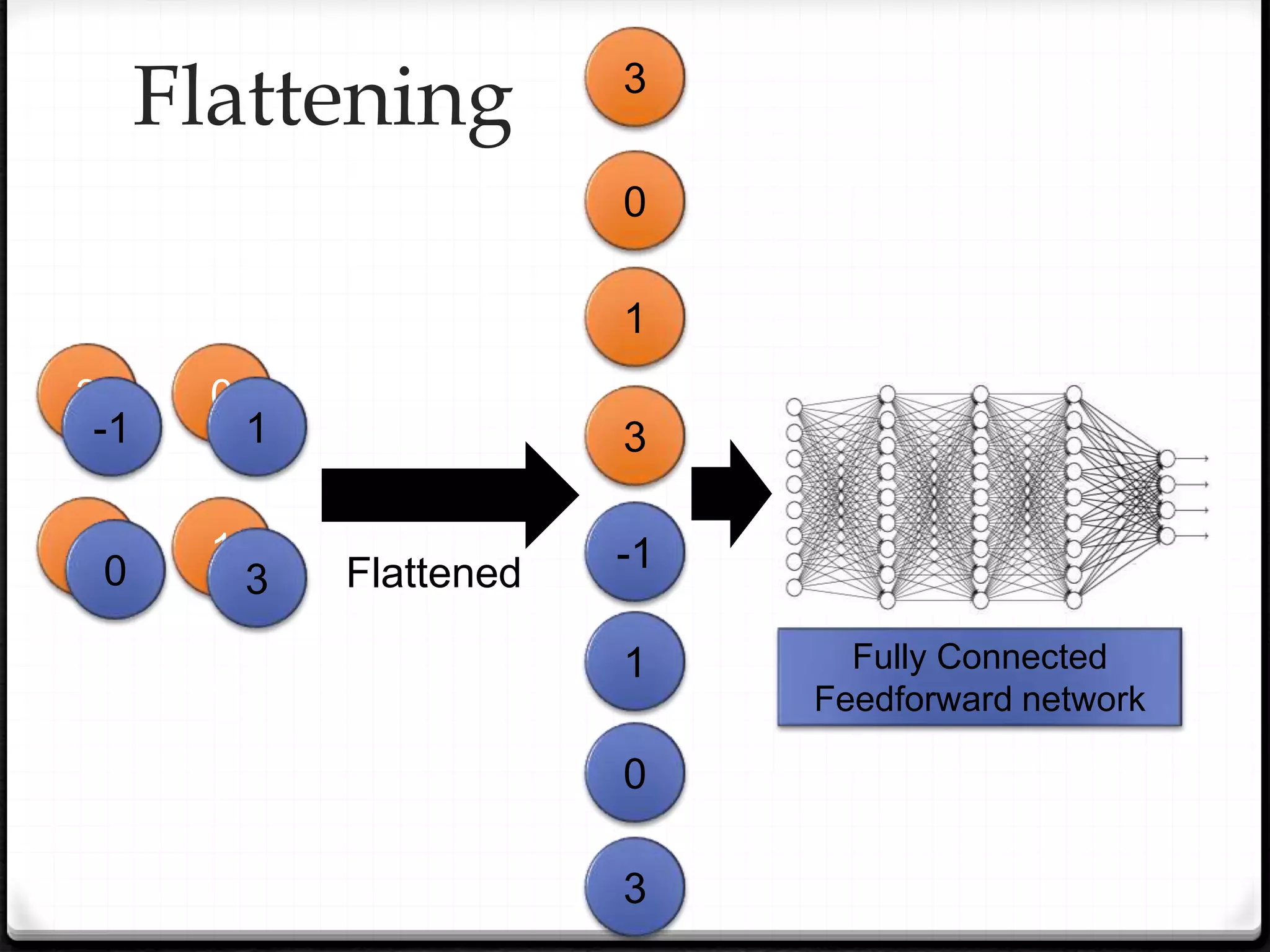
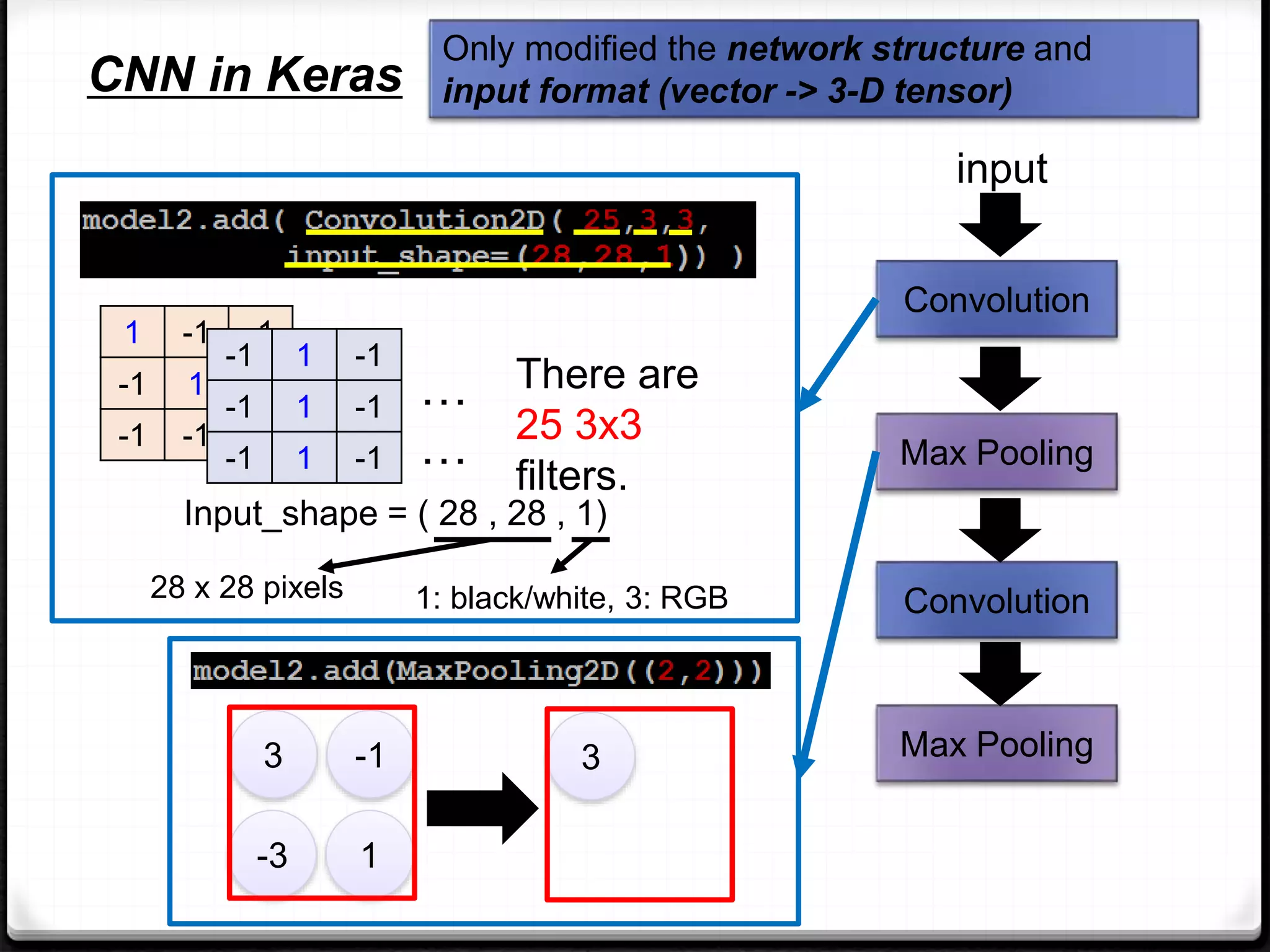
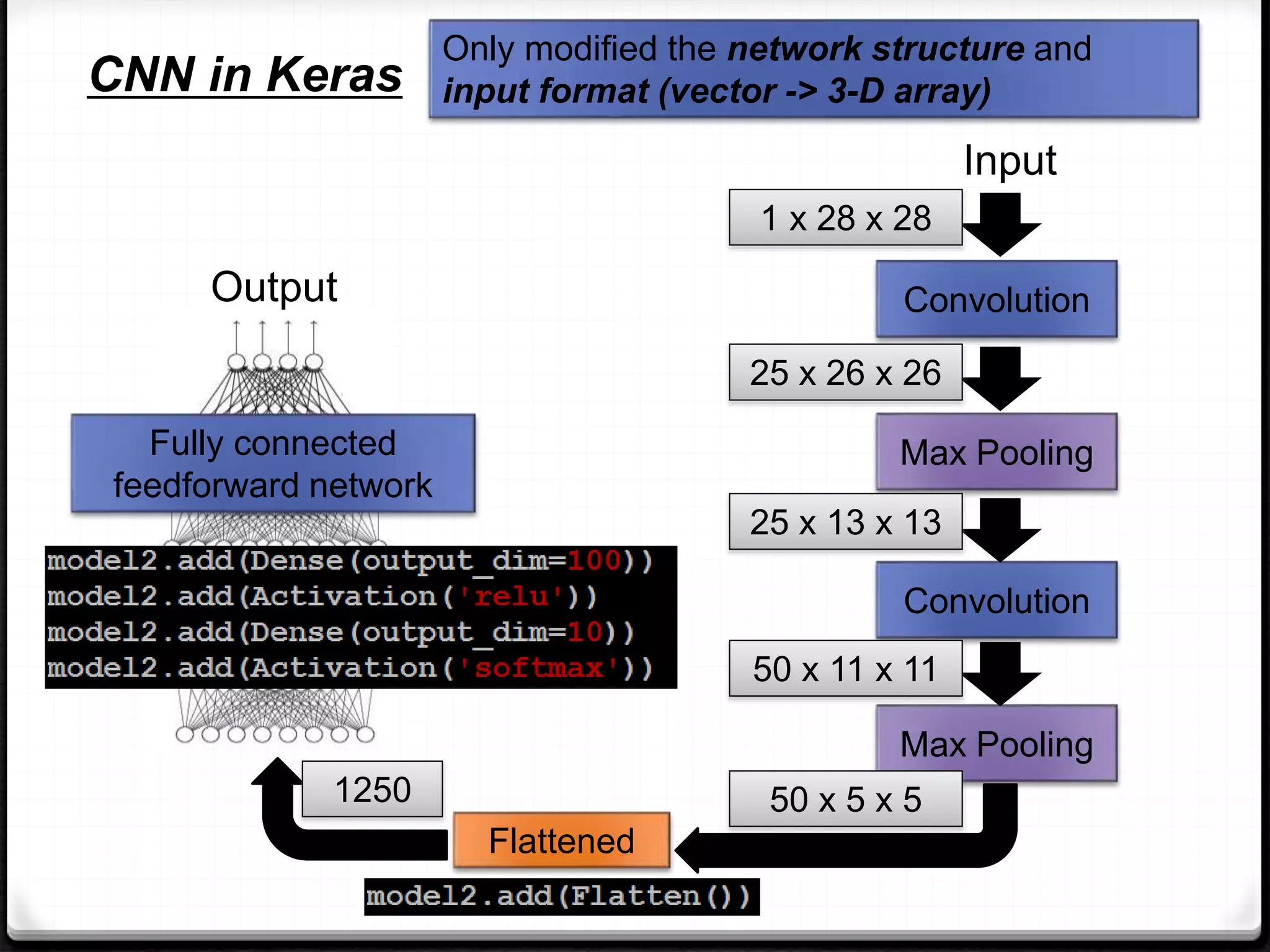
31.  Srivastava, Nitish, et al. "Dropout: a simple way to prevent neural networks from overfitting." Journal
of machine learning research (2014)
 Bergstra, James, and Yoshua Bengio. "Random search for hyper-parameter optimization." Journal of
Machine Learning Research, Feb (2012)
 Kim, Y. “Convolutional Neural Networks for Sentence Classification”, EMNLP (2014)
 Severyn, Aliaksei, and Alessandro Moschitti. "UNITN: Training Deep Convolutional Neural Network for
Twitter Sentiment Classification." SemEval@ NAACL-HLT (2015)
 Cho, Kyunghyun, et al. "Learning phrase representations using RNN encoder-decoder for statistical
machine translation." EMNLP (2014)
 Ilya Sutskever et al. “Sequence to sequence learning with neural networks.” NIPS (2014)
 Bahdanau et al. "Neural machine translation by jointly learning to align and translate." ICLR (2015)
 Gal, Y., Islam, R., Ghahramani, Z. “Deep Bayesian Active Learning with Image Data.” ICML (2017)
 Nair, V., Hinton, G.E. “Rectified linear units improve restricted boltzmann machines.” ICML (2010)
 Ronan Collobert, et al. “Natural language processing (almost) from scratch.” JMLR (2011)
 Kumar, Shantanu. "A Survey of Deep Learning Methods for Relation Extraction." arXiv preprint
arXiv:1705.03645 (2017)
 Lin et al. “Neural Relation Extraction with Selective Attention over Instances” ACL (2016) [code]
 Zeng, D.et al. “Relation classification via convolutional deep neural network”. COLING (2014)
 Nguyen, T.H., Grishman, R. “Relation extraction: Perspective from CNNs.” VS@ HLT-NAACL. (2015)
 Zhang, D., Wang, D. “Relation classification via recurrent NN.” -arXiv preprint arXiv:1508.01006 (2015)
 Zhou, P. et al. “Attention-based bidirectional LSTM networks for relation classification . ACL (2016)
 Mike Mintz et al. “Distant supervision for relation extraction without labeled data.” ACL- IJCNLP (2009)
References

32. https://giphy.com/gifs/thanks-thank-you-thnx-3o6ozuHcxTtVWJJn32/download