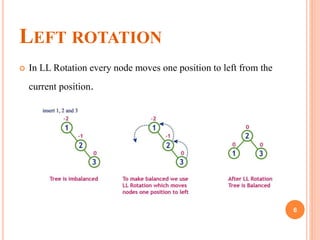
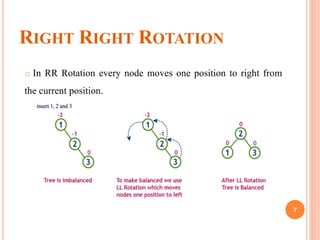
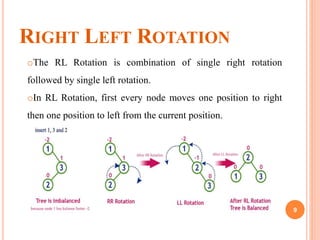
This document discusses AVL trees, which are self-balancing binary search trees. AVL trees balance themselves by performing rotations when nodes are inserted or removed, in order to keep the balance factor of every node between -1 and 1. The balance factor is calculated as the height of the left subtree minus the height of the right subtree. There are four types of rotations - left, right, left-right, and right-left - that are used to rebalance the tree as needed during operations.

1. DATA STRUCTURES
AVL TRESS
B.ABINAYA BHARATHI M.Sc[Cs&IT]
NADAR SARASWATHI COLLEGE OF ARTS AND SCIENCE
THENI
1

2. AVL TREES
 AVL tree is a self-balancing Binary Search Tree
 AVL tree balances itself by making rotations when the tree
becomes unbalanced.
 when inserting a element in binary search tree ,The tree
becomes a gigantic line.
 if the size of the tree is n elements,
 performing each insertion takes n operations.
 Performing all n insertions takes roughly n2
operations. 2

3. BALANCE FACTOR
 In a binary tree the balance factor of a node N is
used
 Balance Factor(N) = Height( RightSubtree(N) ) –
Height( LeftSubtree(N) )
 Balance Factor(N) ∈ {–1,0,+1}
3

4. ROTATION
 To balance itself, an AVL tree may perform the following four
kinds of rotations −
 Left rotation
 Right rotation
 Left-Right rotation
 Right-Left rotation
 The first two rotations are single rotations
 The next two rotations are double rotations. 4

5. ROTATIONS IN AVL TREES
5

6. LEFT ROTATION
 In LL Rotation every node moves one position to left from the
current position.
6

7. RIGHT RIGHT ROTATION
o In RR Rotation every node moves one position to right from
the current position.
7

8. LEFT RIGHT ROTATION
o The LR Rotation is combination of single left rotation
followed by single right rotation.
o In LR Rotation, first every node moves one position to left
then one position to right from the current position.
8

9. RIGHT LEFT ROTATION
oThe RL Rotation is combination of single right rotation
followed by single left rotation.
oIn RL Rotation, first every node moves one position to right
then one position to left from the current position.
9

10. THANK YOU
10