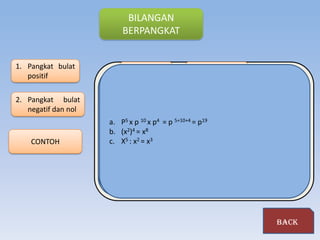
Dokumen ini membahas materi operasi bentuk pangkat, akar, dan logaritma dalam matematika, serta tujuan pembelajaran yang mencakup penyederhanaan bentuk bilangan dan identifikasi jenis bilangan. Siswa diharapkan dapat melakukan berbagai operasi aljabar terkait dan merasionalkan penyebut pecahan. Terdapat juga contoh soal evaluasi untuk mengukur pemahaman konsep tersebut.