CSP2014 Predictive SPC

2/7/2014 A. Gilgur & J. Ferrandiz. Predictive SPC 1
Alex Gilgur, Josep Ferrandiz
ASA Conference on Statistical Practice
Tampa, FL. February 2014

Outline
• SPC = Statistical Process Control
• The Fishbone of SPC
• Traditional SPC
• Six Sigma
• Predictive SPC:
– Univariate
– Multivariate

2/7/2014
A. Gilgur & J. Ferrandiz. Predictive SPC
3
1968

•Artificial Intelligence
•Predictive Analytics
•Data Mining
•Machine Learning

2/7/2014
5
SPC
Specifications
Target
What to measure?
Science / Engineering / Math
Domain
Upper Spec Limit
Lower Spec Limit
Distribution
Stationarity
Process Dynamics
Dependencies
The Fishbone of SPC

Setting Specs is an optimization problem
2/7/2014 6
p
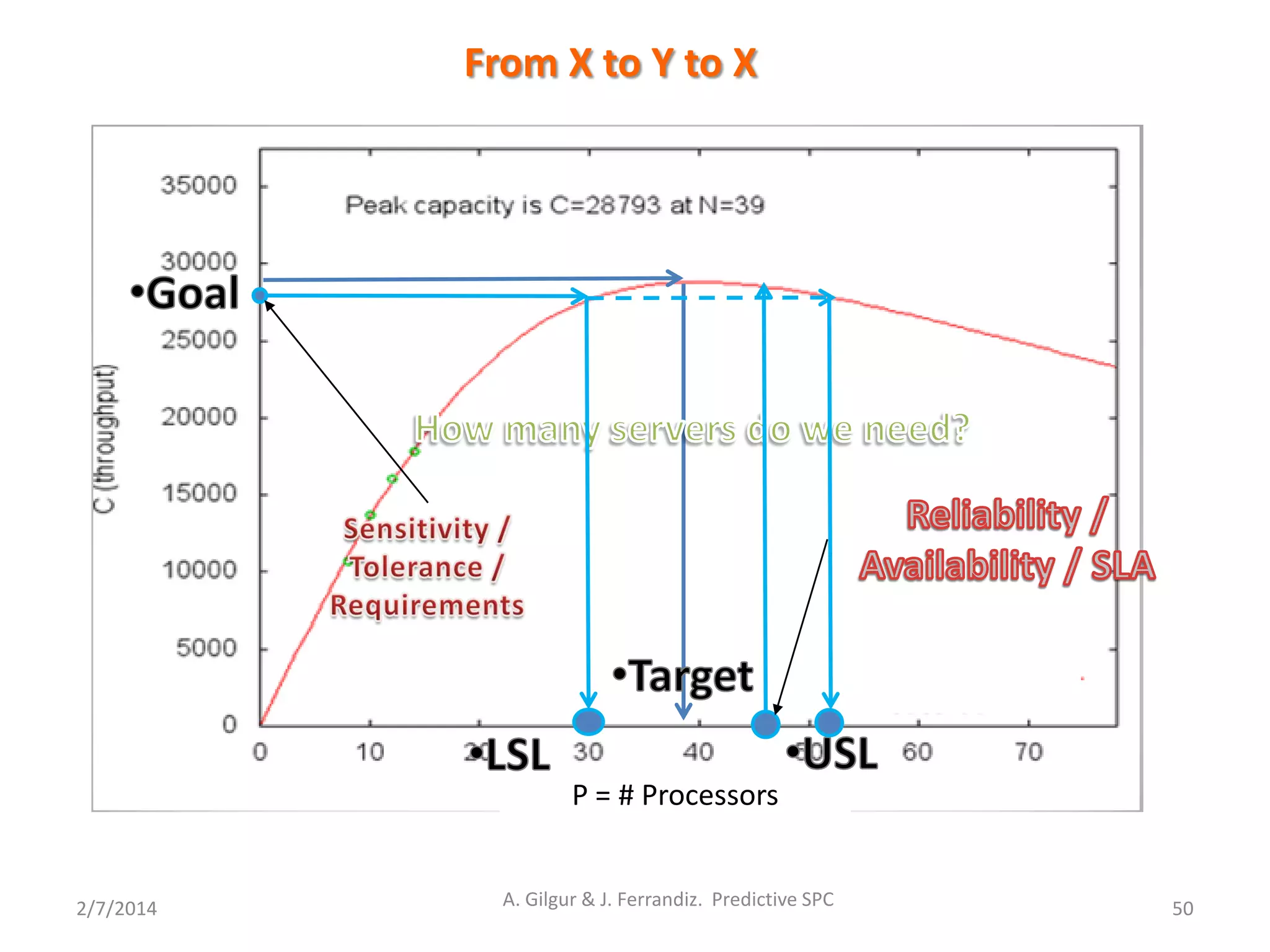
Servers = argmax (Revenue |Budget)
Revenue = f[Throughput (Servers, SW, Budget)]
Servers = argmin (Budget | Revenue)
•Throughput = t (UX)
•Revenue = r (Throughput)
•Budget = f(SW, Servers)
Constraints:
•Domain
•Budget ≤ B
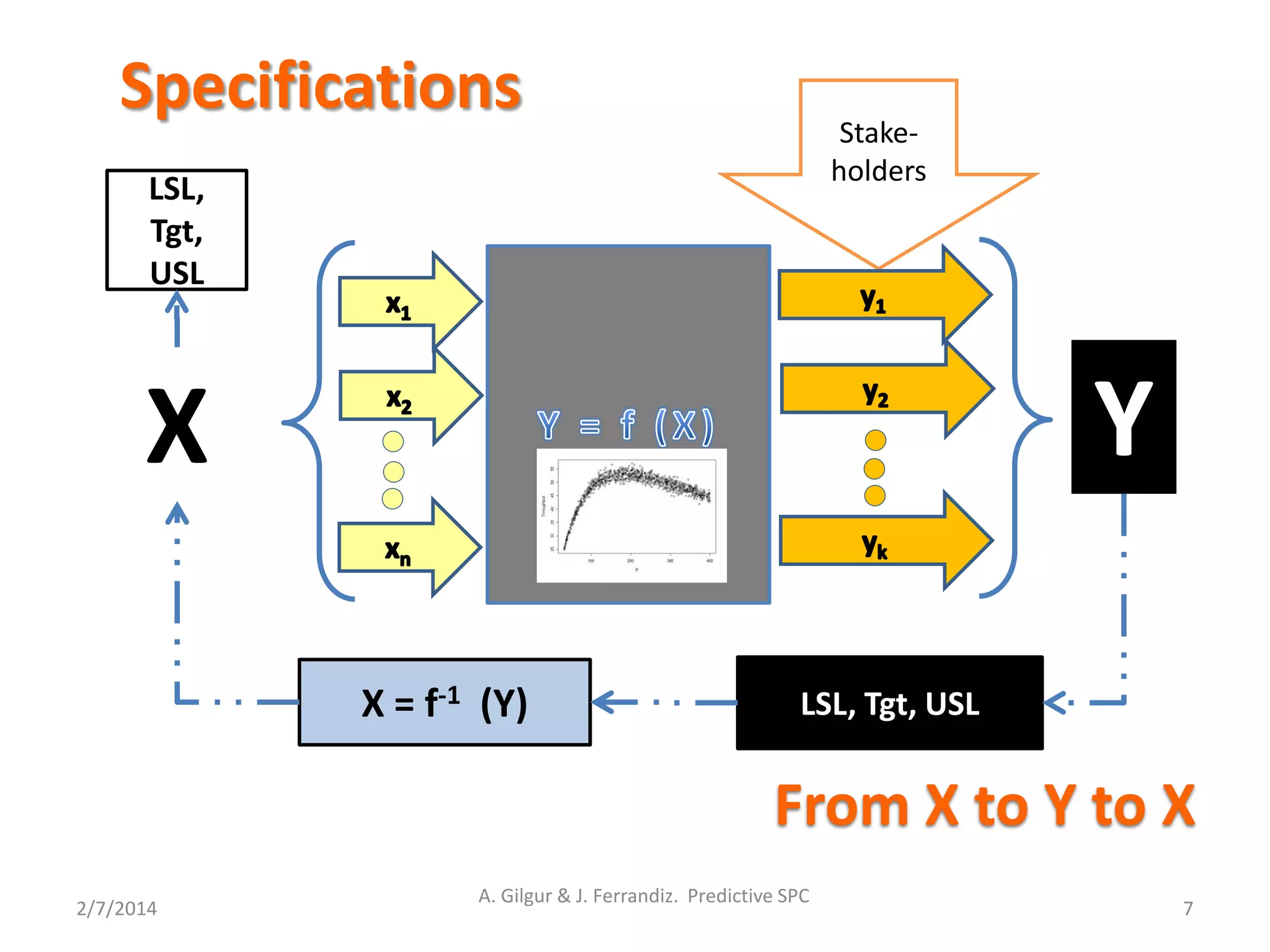
The business drives the specs

Specifications
2/7/2014 7
Stake-
holders
X Y
LSL, Tgt, USLX = f-1 (Y)
LSL,
Tgt,
USL
From X to Y to X

Domain
2/7/2014
8

“Knobs” to turn?
2/7/2014
9
Specifications
Upper Spec Limit
Target
Lower Spec Limit
Domain
Science/Engineering/Math
What to measure?
Closing the loop
Specs to adjust?
Process Dynamics
Stationarity
Distribution
Dependencies

2/7/2014
10
Does External Interaction Only Lead to Improvement?

2/7/2014 11
Process Dynamics: Short-term vs. Long-term
Timeline
Value(IO/sec,%Util,CPULoad,…)
Day1 Day2 Day3 … … … … … … … … ... Day(N-1) Day(N)
0 0.5 1 1.5 2 2.5 3 3.5 4
1
3
5
7
9
11
13
15
17
HIGH
LOW
Data Collection hides the true distribution

2/7/2014 12
Process Dynamics: Traditional SPC
μ == Target;
μ + 6*σ <= USL;
μ - 6*σ >= LSL;
μ
σ
LCL UCL
IDEAL CASE: on target; in control; within the specifications
LSL USL
Target

2/7/2014 13
μ
σ
LSL
USL
Target
LCL UCL
SHIFT
μ != Target;
μ + 6*σ > USL;
μ - 6*σ >= LSL;
REAL CASE # 1: off target; in control; out of the specifications
P-value
Process Dynamics: a Shift
1) Negotiate specs
2) Change the process

2/7/2014
Process Dynamics: a Change in Variance
14
μ != Target;
μ + 6*σ > USL;
μ - 6*σ > LSL;
REAL CASE #2: off target; out of control; out of specifications
μ
σ
LSL
USLTarget
LCL UCL
P-value
1) Negotiate specs
2) Change the process

2/7/2014 15
Bimodal example

• Cp – a measure of the process capability to produce
consistent results:
– Cp = (USL – LSL) / (6 * σ)
– Desired Cp >= 1.0
– High Cp -> “In control”
• Cpk – a measure of the process capability to produce
results that are on target:
– Cpk = Min { ( μ – LSL) / (3 * σ), (USL – μ) / (3 * σ)}
– Desired Cpk >= 1.33
– High Cpk -> “In control and On Target”
• Cpk > Cp > 1.33 -> “In Control, On Target”
• Cpk < Cp < 1.0 -> “Out of Control, Off Target”
2/7/2014 16
SPC Measures

2/7/2014 17
SPC Measures:
Another way to look at it
• Z –measure of process capability to produce results within specs:
– Zlower = (μ – LSL) / σ,
– Zupper = (USL – μ) / σ.
– Long-term and short-term Z:
• Typically, desired Zst* = 6
• Zlt = Zst - 1.5
Zst == 2 : 310,000 defects per 1,000,000 opportunities (69%)
Zst == 3 : 67,000 defects per 1,000,000 opportunities (93.3%)
Zst == 6 : 3.45 defects per 1,000,000 opportunities (99.999965%)
Cpk= (1/3) * min (Zlower , Zupper)

Statistical Process Control
2/7/2014 18
• Traditional SPC
• Six Sigma
• Predictive SPC:
– Univariate
– Multivariate

Six Sigma
2/7/2014 19
http://www.isixsigma.com/
1. Define:
i. End Goal
ii. What to measure
iii. How to measure
2. Measure:
i. Gage R&R
ii. Collect data
3. Analyze:
i. Mean? Variance? Shape? All three?
ii. Correlations
4. Improve:
i. Design and Conduct Experiments
ii. Analyze the results
5. Control:
i. SPC
ii. Education & Training
iii. $avings

Statistical Process Control
• Traditional SPC
• Six Sigma
• Why is it not Good Enough?
• Predictive SPC:
– Univariate
– Multivariate

Why is SPC / Six Sigma not good enough?
Rapid growth
New product introduction
Agile Development
R&D / Science
… … …
Zst == 2 : 310,000 defects per 1,000,000 opportunities (69%)
Zst == 3 : 67,000 defects per 1,000,000 opportunities (93.3%)
Zst == 6 : 3.45 defects per 1,000,000 opportunities (99.999965%)
Manufacturing
Mechanical / Chemical
Semiconductor
Food
Pharmaceutical
Power Plants
Traffic Engineering
Customer Support
… … …

Why is SPC / Six Sigma not good enough?
 Normal distribution
 Stationary processes
 Well defined LSL, Tgt, USL

Something like this:
2/7/2014
23
Or this:
A chemical process:
•Known Specifications
•Unknown Dynamics
•Non-stationary
A Data Center:
•Unknown Specifications
•Somewhat known Dynamics
•Non-stationary

Time1. Forecast the metric
2. An alternative:
1. Observe the process
2. Is the measurement within predicted interval?
2/7/2014 24
Holt-Winters
ARIMA
Univariate Predictive SPC
… … …

Univariate Predictive SPC: what do we do?
Time
Time
Outlier?
•Do nothing
Start of new pattern?
•Reforecast
•The clock:
•Continue from the beginning?
•Reset at reforecast point?
When do we decide?
Process Dynamics
Stationarity
Distribution
Dependencies

A Business Model
2/7/2014
26
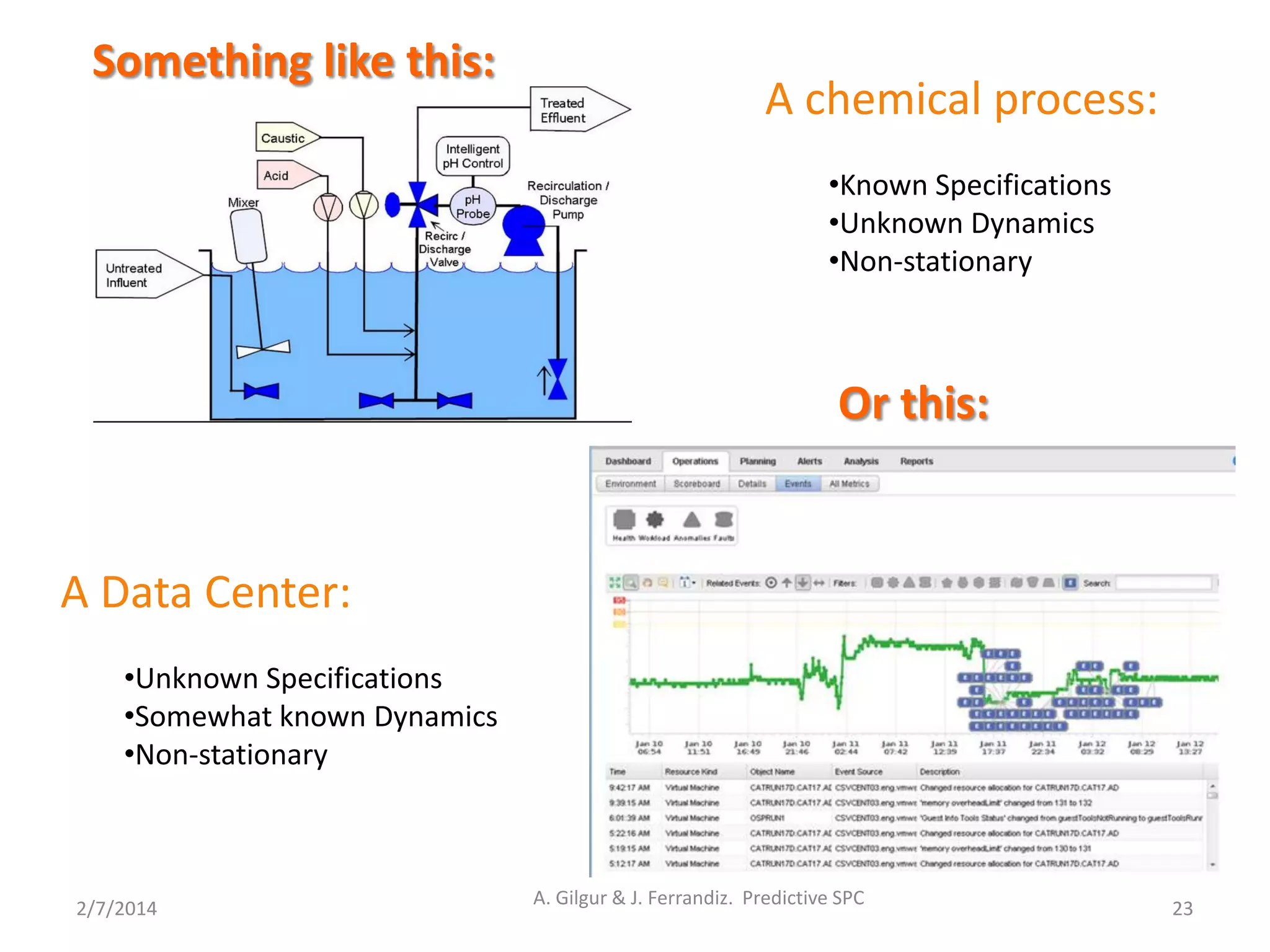
Application DB
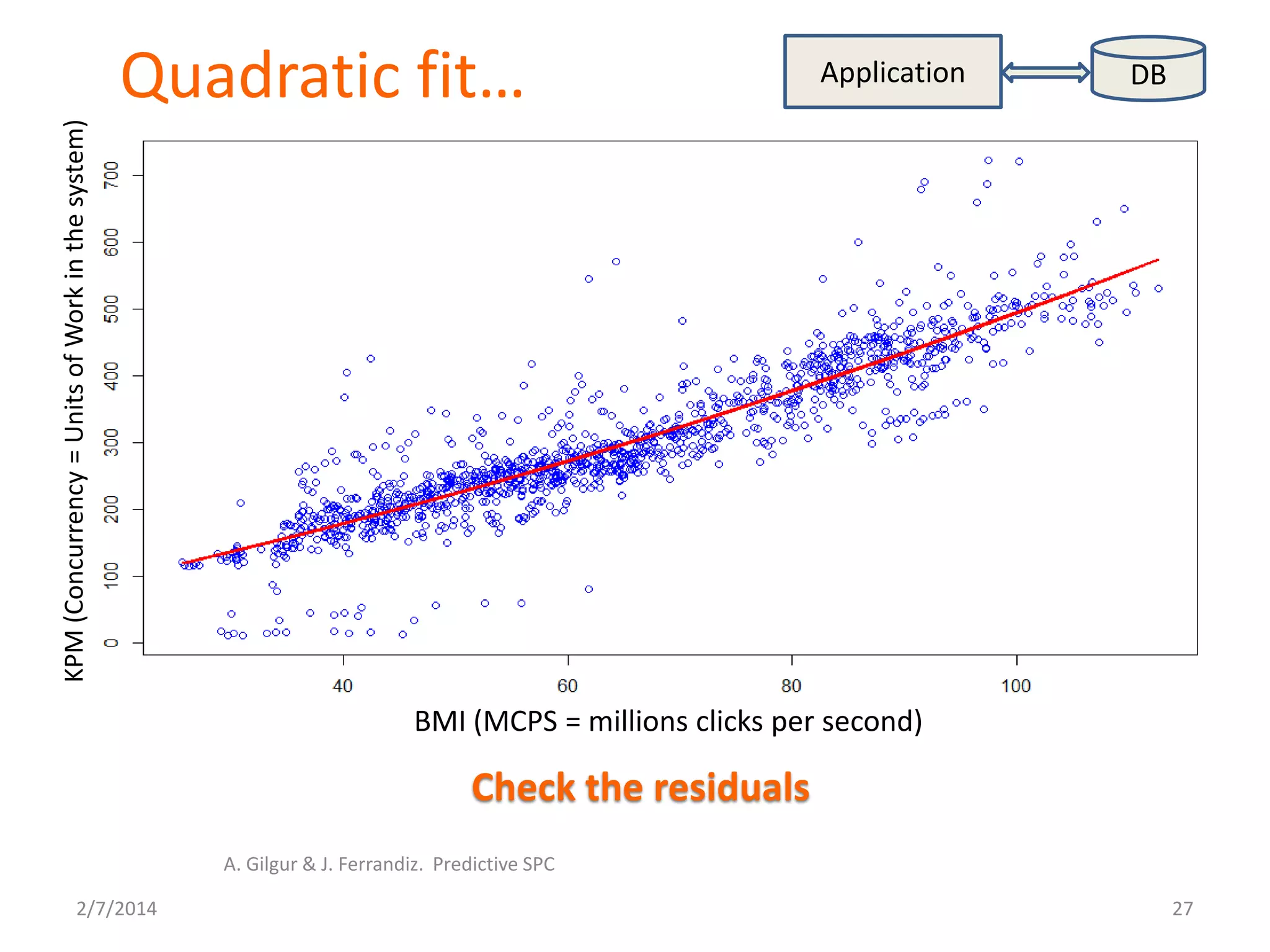
Makes sense to use parabola …
Traffic = # of units of work (worker threads in use) in the system
Little’s Law:
Traffic = Arrival_rate * Processing_time
Arrival_Rate = a * BMI + b
Processing_time = c * Arrival_rate + d
Traffic = (a * BMI + b) * [c * (a * BMI + b) + d]
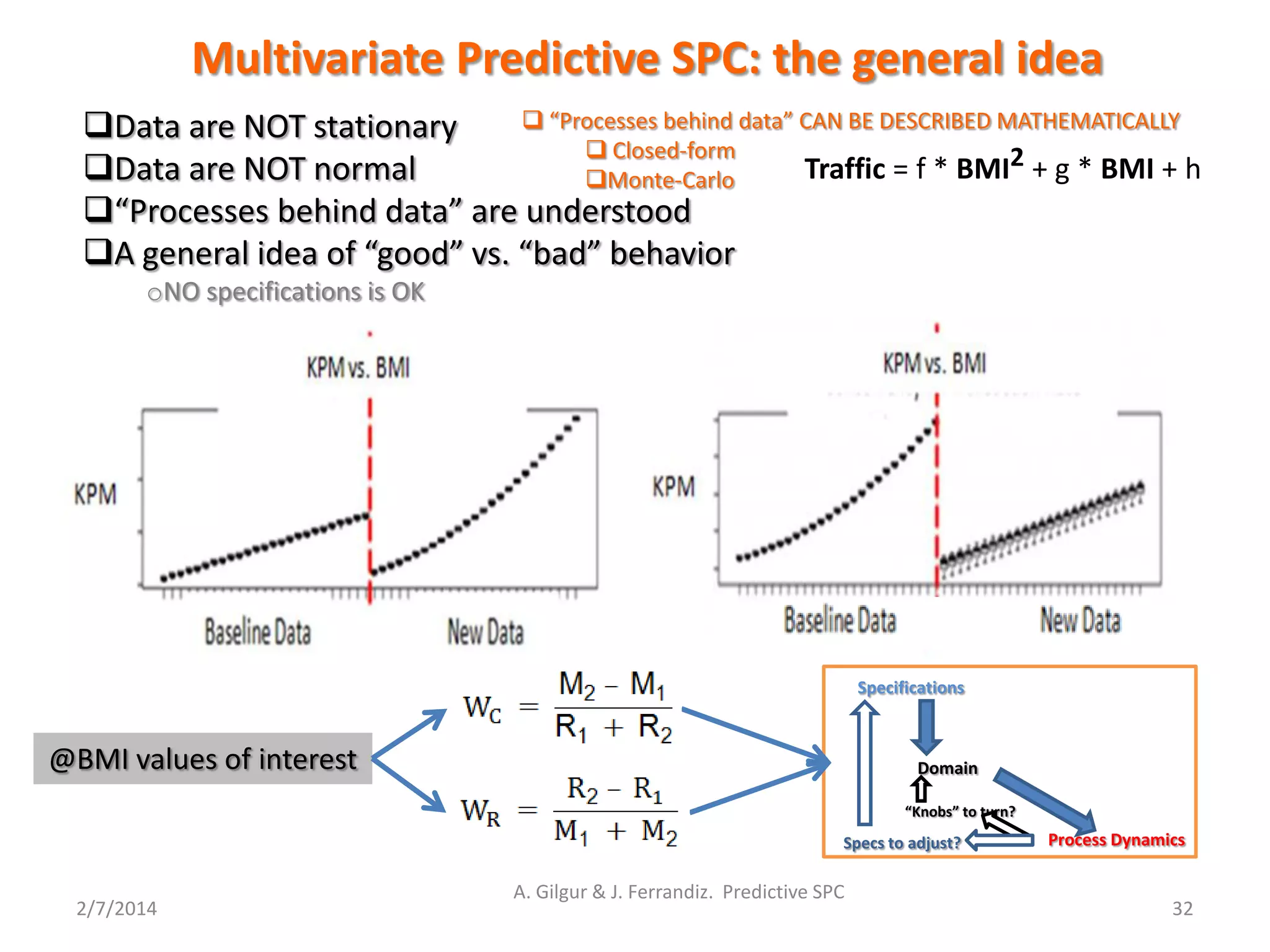
Traffic = f * BMI2 + g * BMI + h
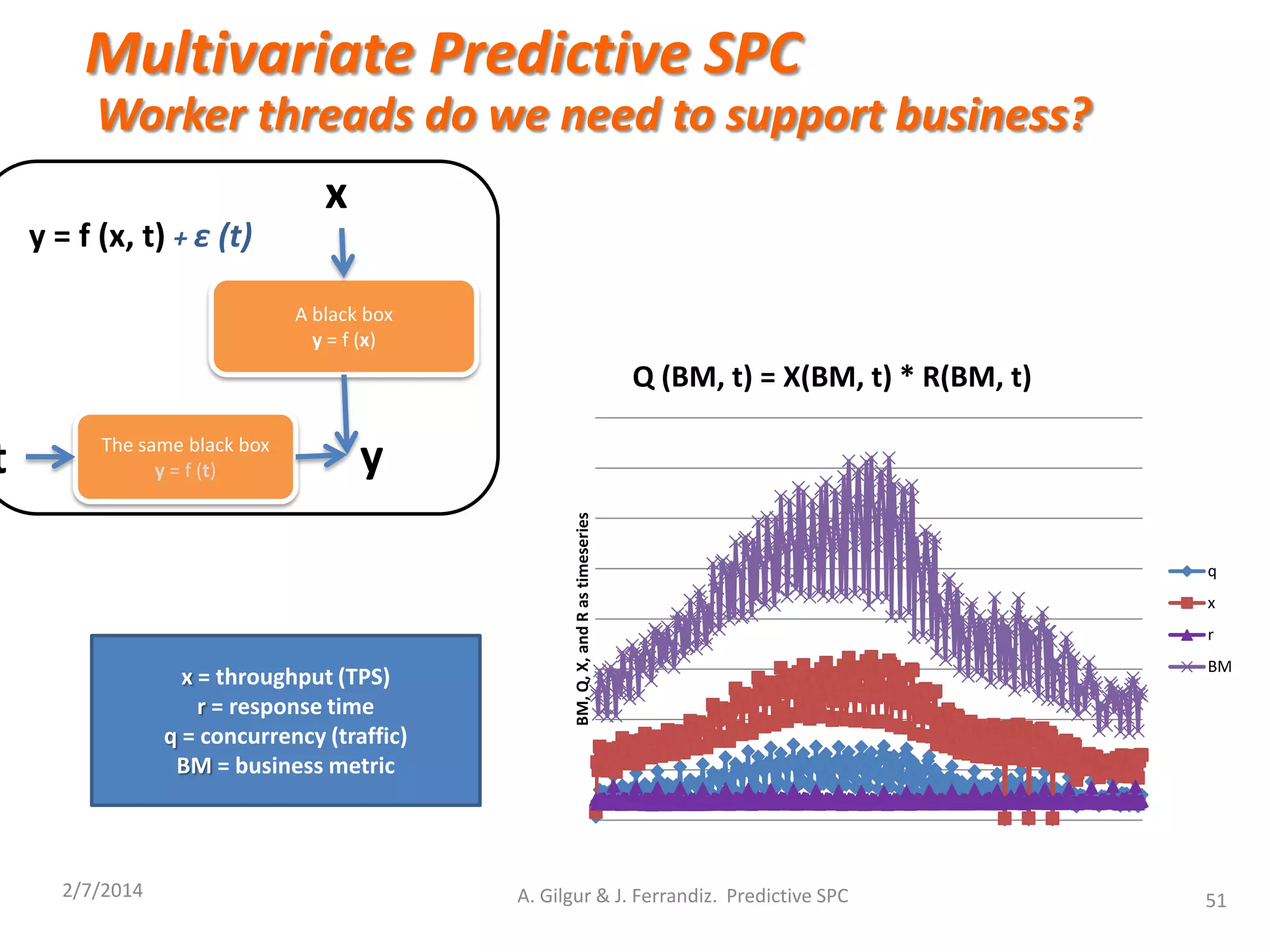
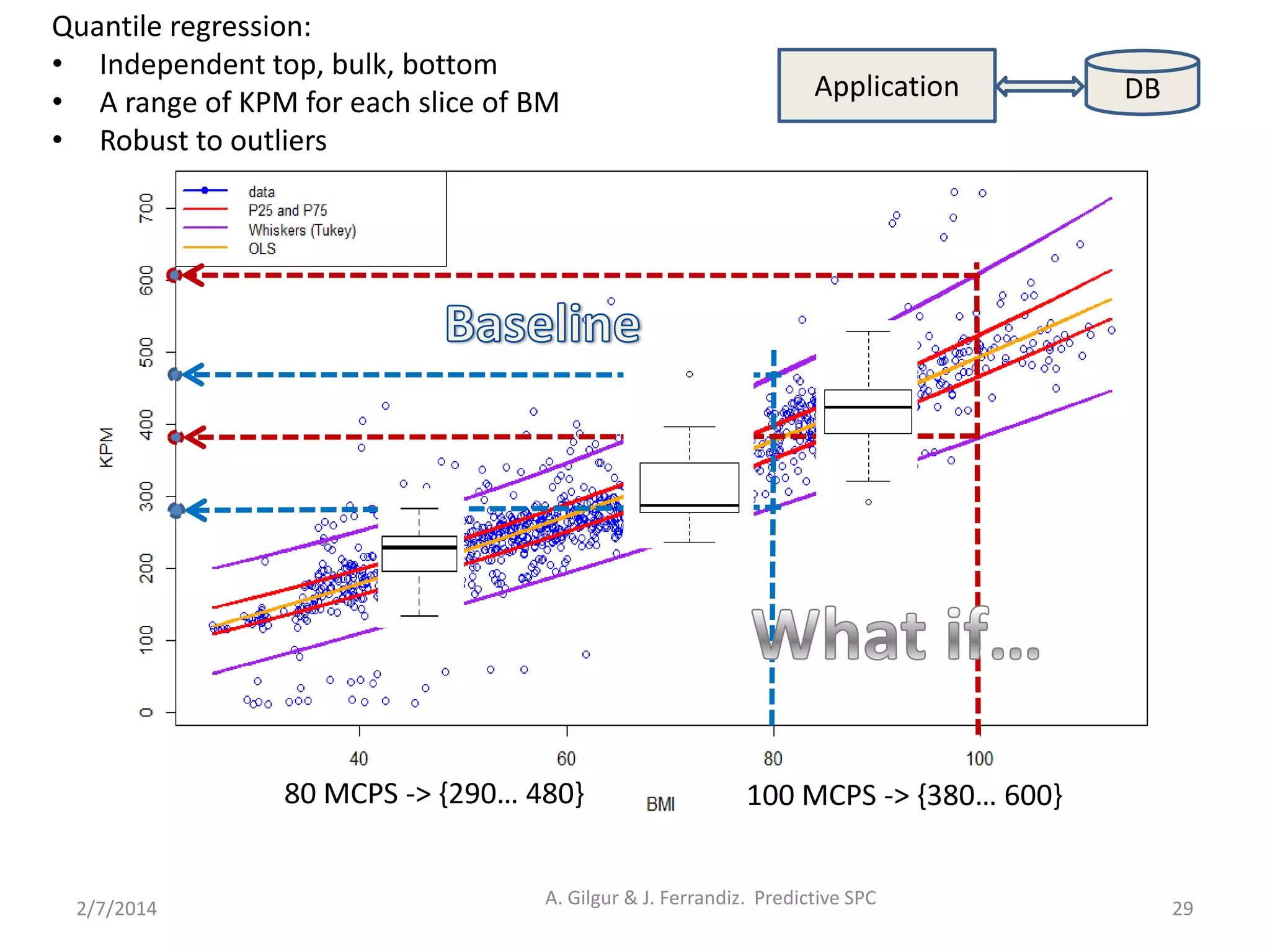
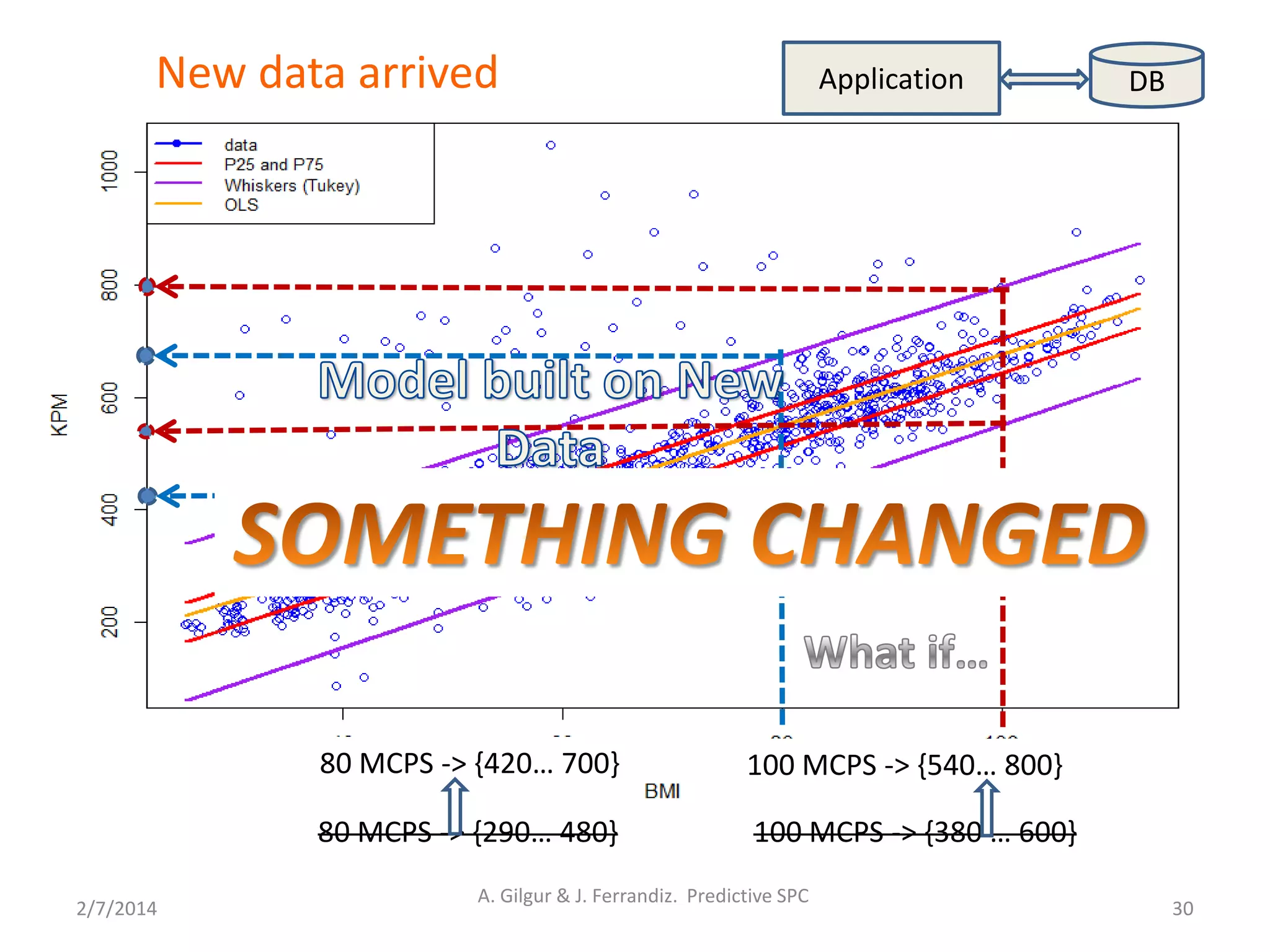
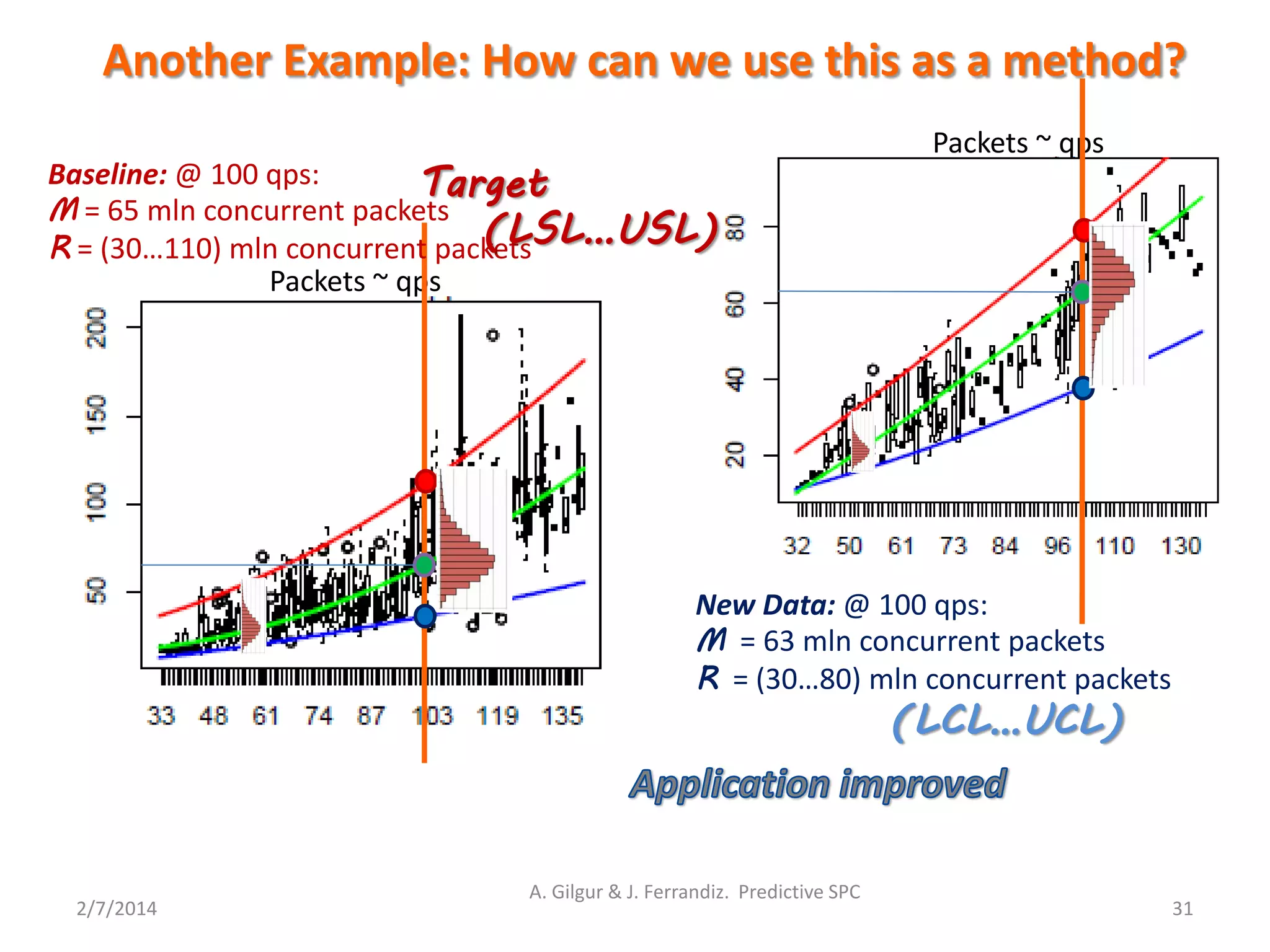
Multivariate Predictive SPC
x = throughput
r = response time
q = # of worker threads
BM = business metric

Quadratic fit…
2/7/2014
27
Application DB
Check the residuals
KPM ~ BMI2 + BMI
BMI (MCPS = millions clicks per second)
KPM(Concurrency=UnitsofWorkinthesystem)

Application DB
The curve fit is a-OK
Outliers
Patterns:
Top != Bulk != Bottom
Residuals…

What’s SPC got to do with it?
2/7/2014
29
Application DB
80 MCPS -> {290… 480} 100 MCPS -> {380… 600}
Quantile regression:
• Independent top, bulk, bottom
• A range of KPM for each slice of BM
• Robust to outliers

80 MCPS -> {290… 480} 100 MCPS -> {380 … 600}
New data arrived
2/7/2014
30
Application DB
80 MCPS -> {420… 700} 100 MCPS -> {540… 800}

Packets ~ qps
Packets ~ qps
Another Example: How can we use this as a method?
2/7/2014
31
Baseline: @ 100 qps:
M = 65 mln concurrent packets
R = (30…110) mln concurrent packets
New Data: @ 100 qps:
M = 63 mln concurrent packets
R = (30…80) mln concurrent packets
Target
(LCL…UCL)
(LSL…USL)

Specifications
Domain
Specs to adjust? Process Dynamics
Multivariate Predictive SPC: the general idea
2/7/2014
32
Data are NOT stationary
Data are NOT normal
“Processes behind data” are understood
A general idea of “good” vs. “bad” behavior
oNO specifications is OK
Traffic = f * BMI2 + g * BMI + h
@BMI values of interest
 “Processes behind data” CAN BE DESCRIBED MATHEMATICALLY
 Closed-form
Monte-Carlo

How can we use it?
Direct KPM-BMI link
ID degraded apps “Knobs” to turn?
Specifications
Domain

•Artificial Intelligence
•Predictive Analytics
•Data Mining
•Machine Learning1968
2014
Predictive SPC

So, how else can we use this as a method?
2/7/2014
35
Business
Metric
# Work Units # Servers

How else can we
use this as a method?
p
Universal
Scalability Law
# Servers
KPM
Specs
Ballast

Summary
• SPC Loop(s):
– The Why
– The What
– The How
• Six Sigma:
– DMAIC
• Next Generation:
– Predictive SPC
• Univariate Predictive SPC: Forecasting
• Multivariate Predictive SPC: Relationships among variables
– A way to stay ahead of the curve
– Domain specific
– Process agnostic
– Expandable, Flexible, and Robust
– An extension of Traditional SPC
– Successfully implemented in IT
Specifications
Domain

Thank you!
www.isixsigma.com
www.amstat.org
www.cmg.org
www.linkedin.com
http://alexonsimanddata.blogspot.com/
http://josepferrandiz.blogspot.com/
“Statistical thinking will one day be as necessary for
efficient citizenship as the ability to read and write.”
- H.G.Wells (1866-1946)

THANK YOU

Appendix
• BACKUP SLIDES

Traditional SPC
2/7/2014
41
HIGH
LOW
0
5
10
15
20
25
30
35
40
1 4 7 10 13 16 19 22 25 28 31 34 37 40 43 46 49 52 55 58 61 64 67 70 73 76 79 82 85 88 91 94 97 100 103 106 109 112 115 118 121
R
0 50 100 150 200 250 300 350 400 450 500
1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
33
35
37
39
0 0.5 1 1.5 2 2.5 3 3.5 4
1
3
5
7
9
11
13
15
17
Date
DailyAvg.
TPS
0
10
20
30
40
50
60
70
1 4 7 10 13 16 19 22 25 28 31 34 37 40 43 46 49 52 55 58 61 64 67 70 73 76 79 82 85 88 91 94 97 100 103 106 109 112 115 118 121
HIGH
LOW
R
Date
Avg.CPU
utilization,%

Alternatives: Entropy-based approach
2/7/2014
42
(IN A
CLOSED
SYSTEM)

2/7/2014
43
Entropy and probabilities
Boltzmann’s Entropy:
Shannon’s Entropy:
∆ H < 0 → external
interaction detected

2/7/2014 44
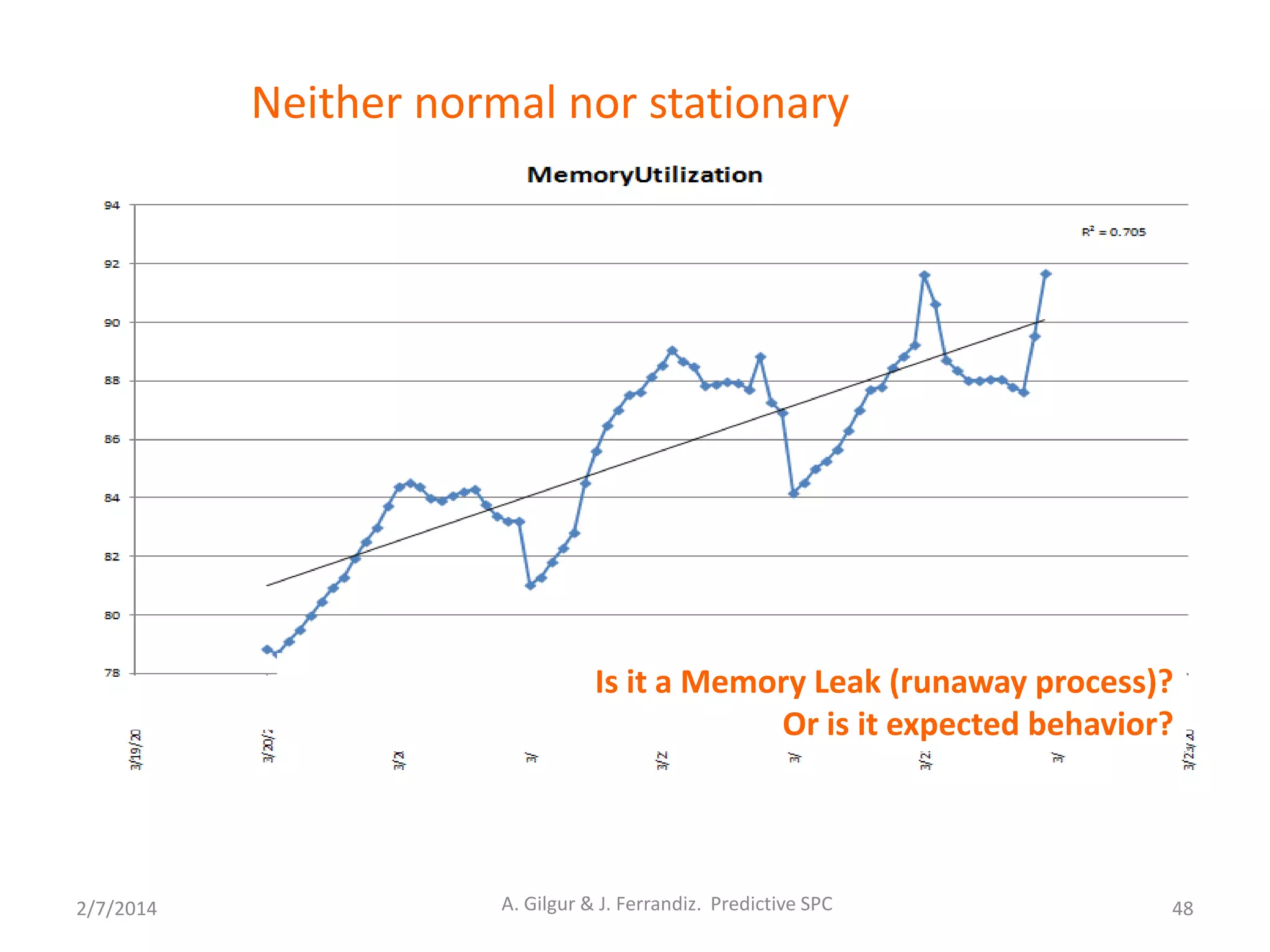
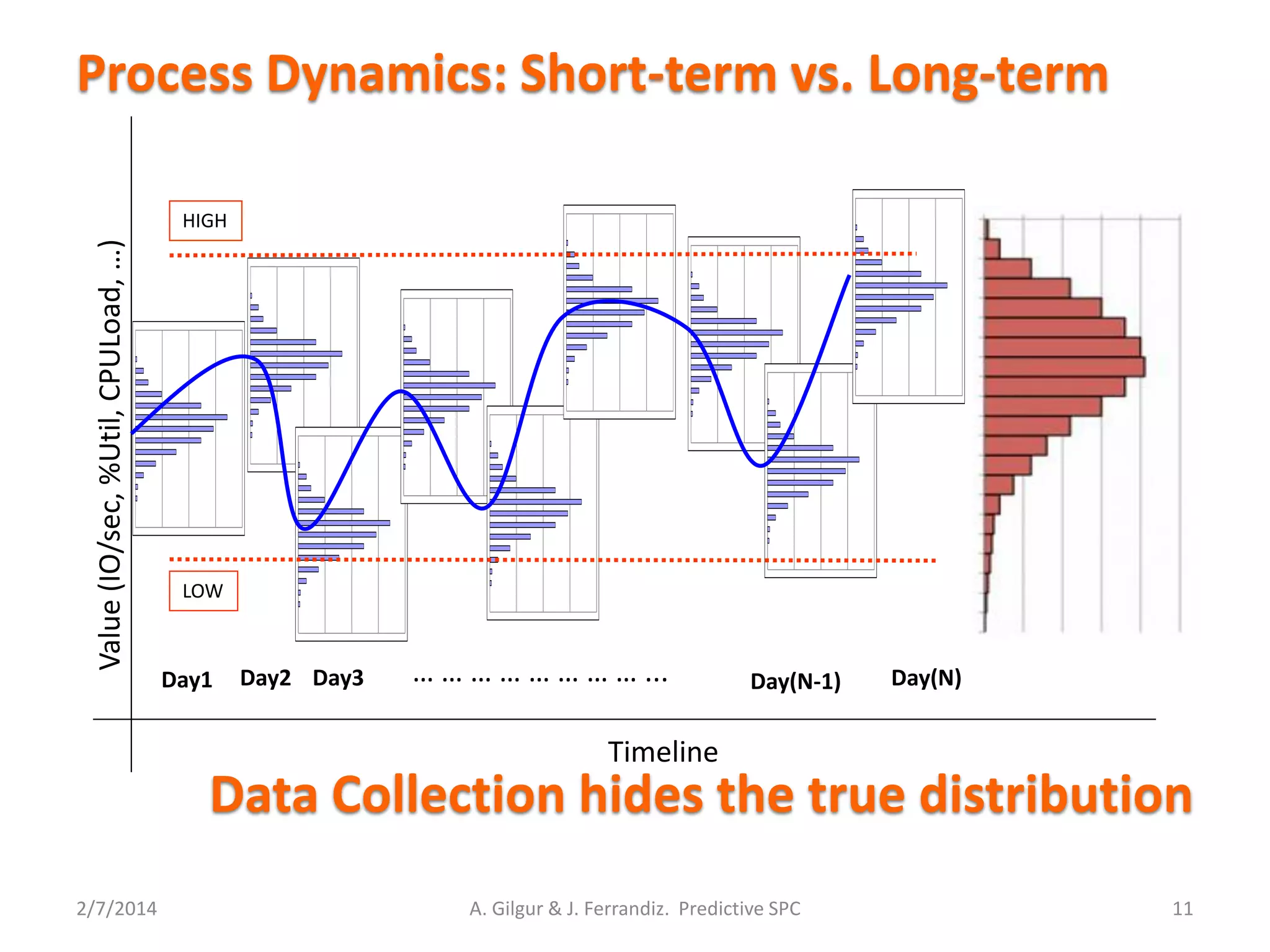
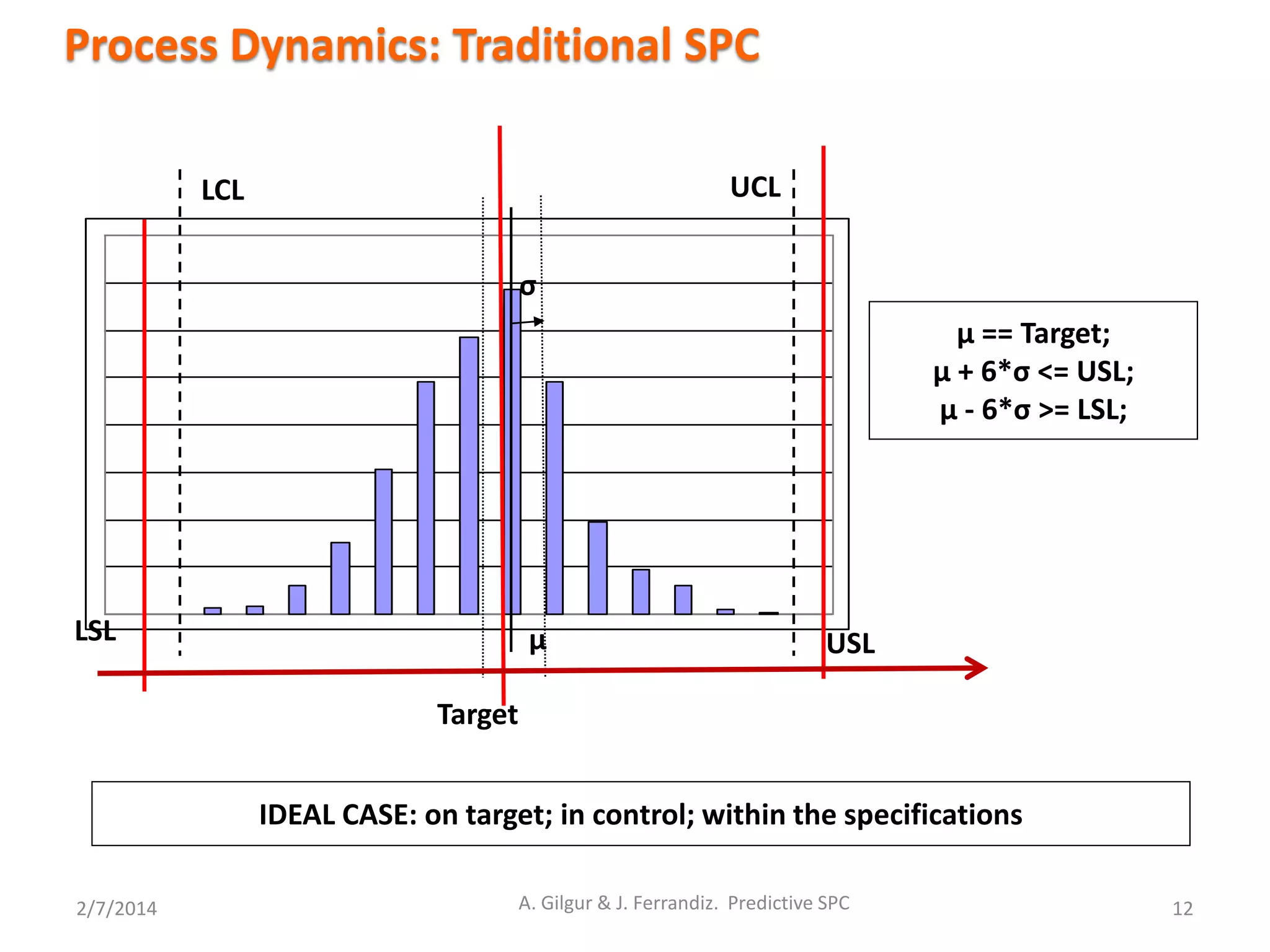
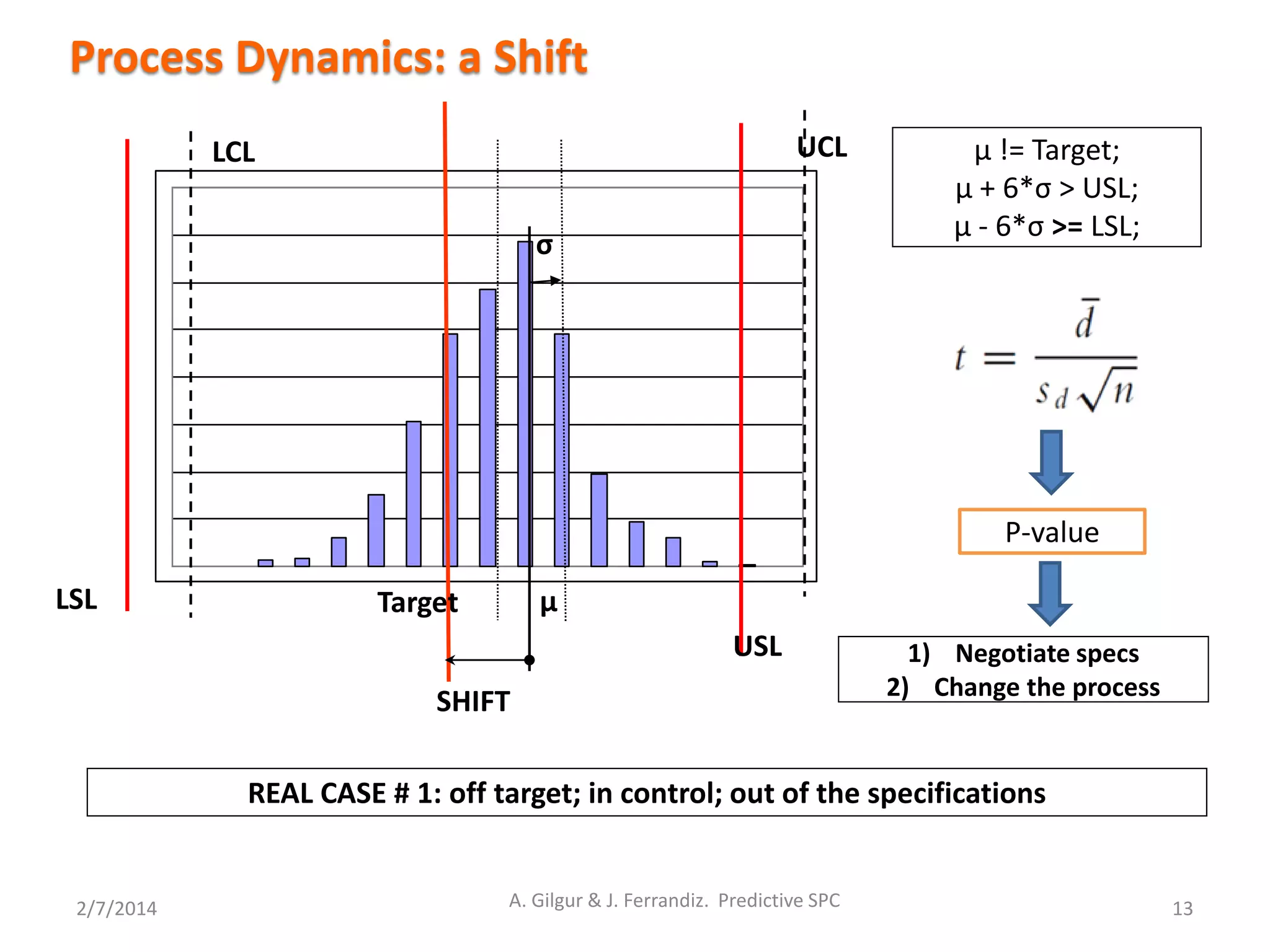
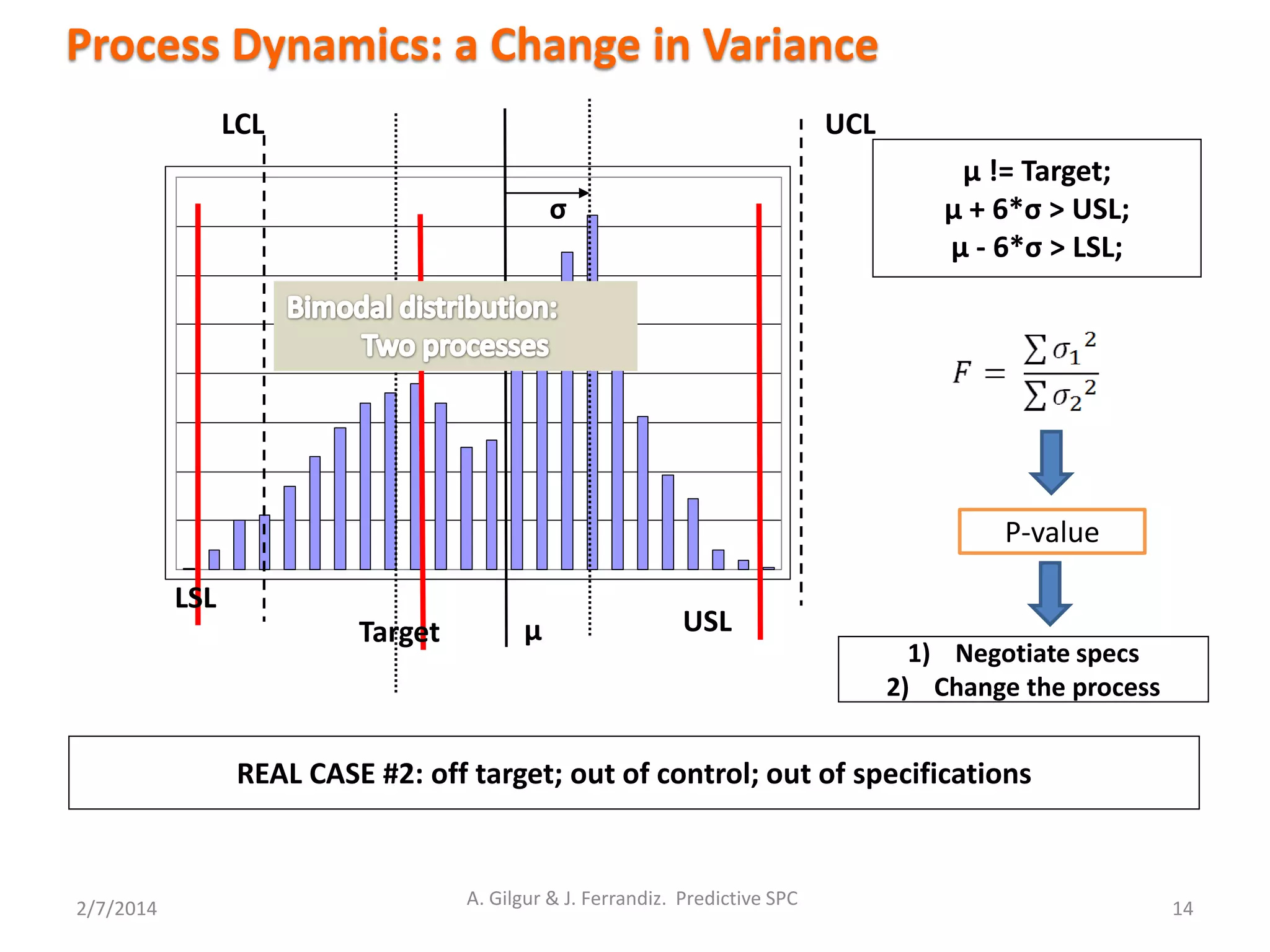
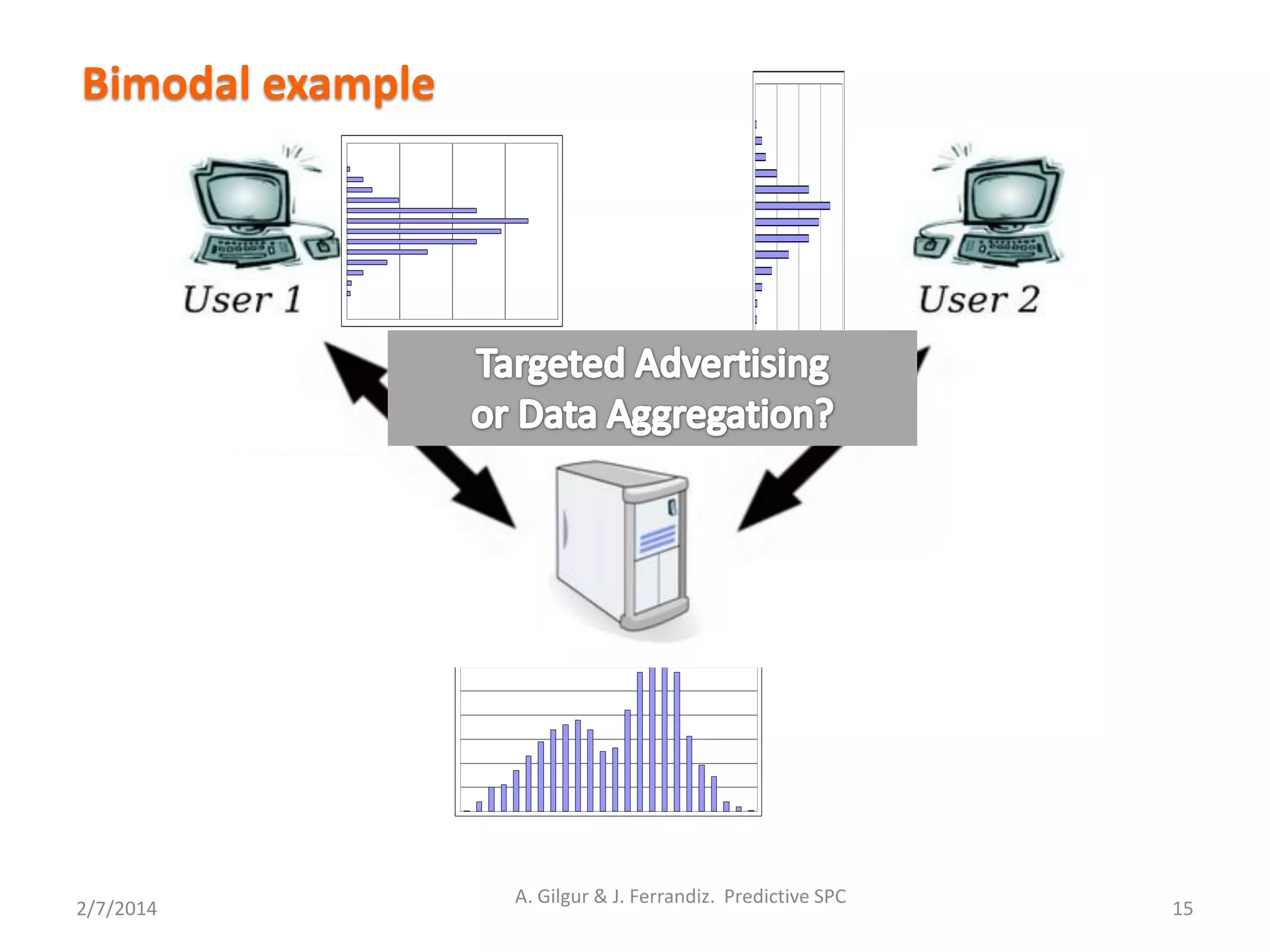
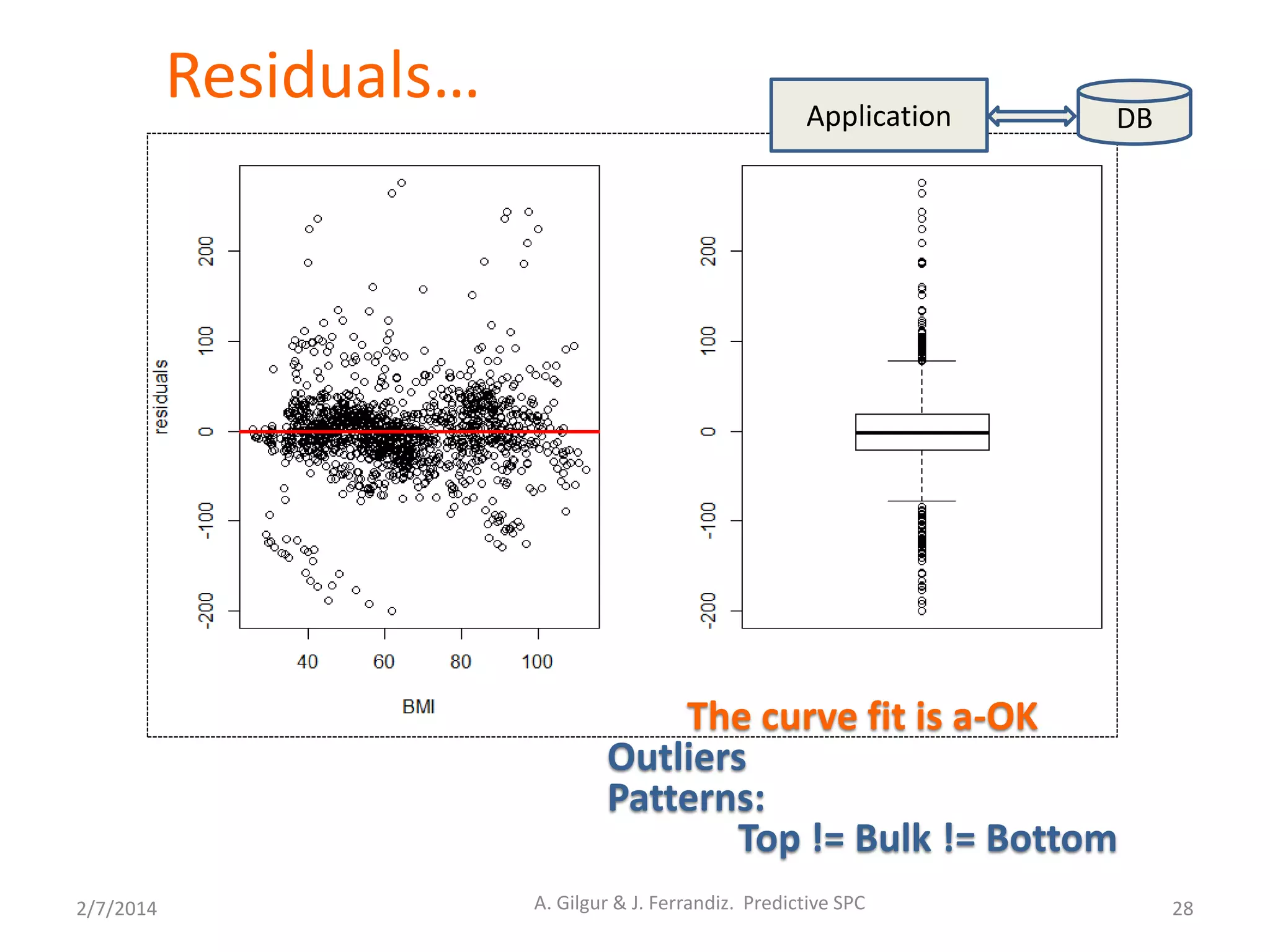
Process Dynamics: A change in variance
Application DB
Server 1
Server 2
Server 3
Server N
Load
Balancer
Server [N+1]
Server [N+2]
Server [N + K]
Load Balancer:
• Has the load variance changed?
P-value

2/7/2014
45
Practical Application: Load Balancer
Application DB
Server 1
Server 2
Server 3
Server NLoad
Balancer
Server [N+1]
Server [N+2]
Server [N + K]
P-value
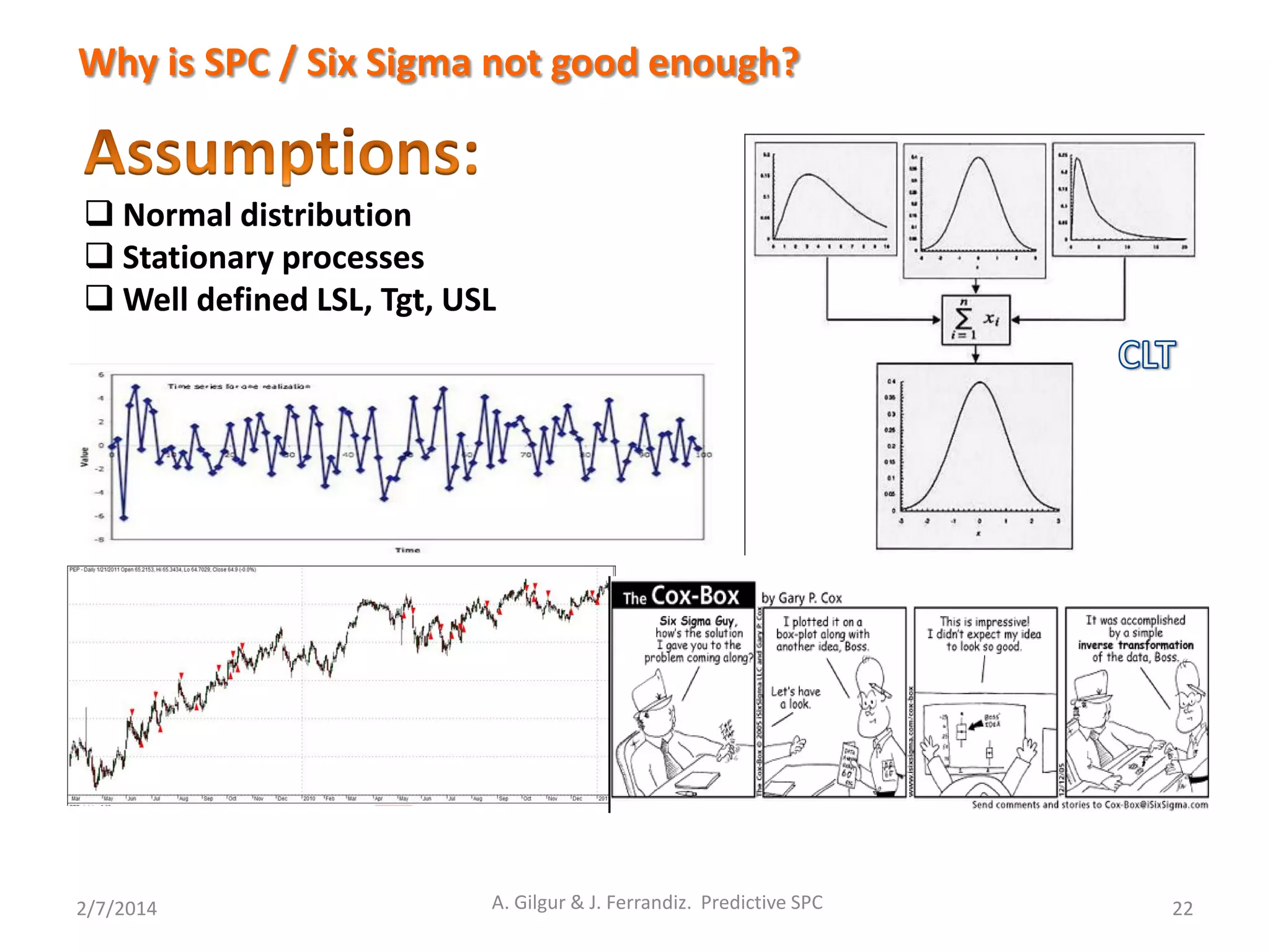
 Normal distribution
 Stationary processes
Xi: Server “i” got the transaction
wear and tear
from within
External
interaction

2/7/2014
46
Does External Interaction Only Lead to Entropy Reduction?

Western Electric Rules
2/7/2014
47
http://en.wikipedia.org/wiki/Western_Electric_rules
http://en.wikipedia.org/wiki/Nelson_rulesNelson Rules

Neither normal nor stationary
Is it a Memory Leak (runaway process)?
Or is it expected behavior?

Why SPC?
• Because it’s cool
• Because it is logical
• Because we like to feel in control
• Because it saves $$
• Because we have the math all figured out
2/7/2014 A. Gilgur & J. Ferrandiz. Predictive SPC
49

P = # Processors
From X to Y to X

2/7/2014 51
A black box
y = f (x)
x
The same black box
y = f (t)t y
y = f (x, t) + ε (t)
BM,Q,X,andRastimeseries
Q (BM, t) = X(BM, t) * R(BM, t)
q
x
r
BM
x = throughput (TPS)
r = response time
q = concurrency (traffic)
BM = business metric
Worker threads do we need to support business?
Multivariate Predictive SPC

CSP2014 Predictive SPC

More Related Content

Viewers also liked

Similar to CSP2014 Predictive SPC

More from Alex Gilgur

Recently uploaded

CSP2014 Predictive SPC