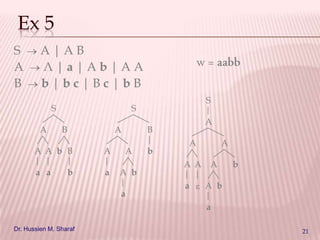
This document introduces parsing and context-free grammars. It discusses how a parser uses a context-free grammar to determine if a program's syntax is correct by building a parse tree. It then provides examples of context-free grammars for simple languages involving parentheses, palindromes, and arithmetic expressions. The document also discusses ambiguity in grammars and ways to eliminate it, such as removing empty productions and avoiding left recursion.

1. WELCOME TO A
JOURNEY TO
CS419
Dr. Hussien Sharaf
Computer Science Department
dr.sharaf@from-masr.com

2. Dr. Hussien M. Sharaf
PART ONE
2

3. PARSING


A parser gets a stream of
tokens from the scanner, and
determines if the syntax
(structure) of the program is
correct according to the
(context-free) grammar of the
source language.
Then, it produces a data
structure, called a parse tree or
an abstract syntax tree, which
describes the syntactic
structure of the program.
Dr. Hussien M. Sharaf
Stream of tokens
parser
Parse/syntax tree
3

4. CFG





A context-free grammar is a notation for
defining context free languages.
It is more powerful than finite automata or
RE’s, but still cannot define all possible
languages.
Useful for nested structures, e.g., parentheses
in programming languages.
Basic idea is to use “variables” to stand for
sets of strings.
These variables are defined recursively, in
terms of one another.
Dr. Hussien M. Sharaf
4

5. CFG FORMAL DEFINITION
C =(V, Σ, R, S)
 V: is a finite set of variables.
 Σ: symbols called terminals of the
alphabet of the language being defined.
 S V: a special start symbol.
 R: is a finite set of production rules of the
form A→ where A
V,  (V Σ)

Dr. Hussien M. Sharaf
5

6. CFG -1





Define the language { anbn | n > 1}.
Terminals = {a, b}.
Variables = {S}.
Start symbol = S.
Productions =



S → ab
S → aSb
Summary
S
→ ab
 S → aSb
Dr. Hussien M. Sharaf
6

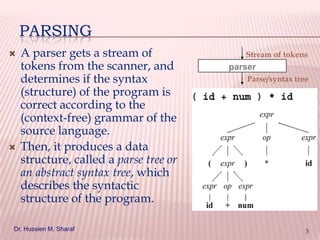
7. DERIVATION



We derive strings in the language of a CFG by
starting with the start symbol, and repeatedly
replacing some variable A by the right side of one of
its productions.
Derivation example for “aabb”
Using S→ aSb
generates uncompleted string that still has a nonterminal S.

Then using S→ ab to replace the inner S
 Generates

“aabb”
S aSb aabb ……[Successful derivation of aabb]
Dr. Hussien M. Sharaf
7

8. CFG -1 : BALANCED-PARENTHESES
Prod1 S → (S)
Prod2 S → ()
 Derive the string ((())).
S → (S)
…..[by prod1]
→ ((S))
…..[by prod1]
→ ((()))
…..[by prod2]
Dr. Hussien M. Sharaf
8

9. CFG -2 : PALINDROME
Describe palindrome of a’s and b’s using
CFG
 1] S → aSa
2] S → bSb
 3] S → Λ

Derive “baab” from the above grammar.
 S → bSb
[by 2]
→ baSab
[by 1]
→ ba ab
[by 3]

Dr. Hussien M. Sharaf
9

10. CFG -3 : EVEN-PLAINDROME


i.e. {Λ, ab, abbaabba,… }
S → aSa| bSb| Λ
Derive abaaba
S
a
S
a
b
S
b
a
S
a
Λ
Dr. Hussien M. Sharaf
10

11. CFG – 4
Describe anything (a+b)* using CGF
1] S → Λ
2] S → Y
3] Y→ aY
4] Y → bY
5] Y →a
6] Y→ b

Derive “aab” from the above grammar.
 S → aY
[by 3]
Y → aaY
[by 3]
Y → aab
[by 6]

Dr. Hussien M. Sharaf
11

12. CFG – 5
1] S → Λ
2] S → aS
3] S→ bS
Derive “aa” from the above grammar.
 S → aS
[by 2]
→ aaS
[by 2]
→ aa
[by 1]

Dr. Hussien M. Sharaf
12

13. Dr. Hussien M. Sharaf
PART TWO
13

14. Parsing





CFG grammar is about categorizing the statements
of a language.
Parsing using CFG means categorizing a certain
statements into categories defined in the CFG.
Parsing can be expressed using a special type of
graph called Trees where no cycles exist.
A parse tree is the graph representation of a
derivation.
Programmatically; Parse tree can be represented as a
dynamic data structure using a single root node.
Dr. Hussien M. Sharaf
14

15. Parse tree
(1)A vertex with a label which is a
Non-terminal symbol is a parse tree.
(2) If A → y1 y2 … yn is a rule in R,
then the tree
A
y
1
y
2
...
y
n
is a parse tree.
Dr. Hussien M. Sharaf
15

16. Ambiguity
A grammar can generate the same string in
different ways.
 Ambiguity occurs when a string has two or
more leftmost derivations for the same CFG.
 There are ways to eliminate ambiguity such
as using Chomsky Normal Form (CNF)
which does n’t use Λ.
 Λ cause ambiguity.

Dr. Hussien M. Sharaf
16

17. Ex 1
Deduce CFG of addition and parse the
following expression 2+3+5
 1] S→S+S|N
 2] N→1|2|3|4|5|6|7|8|9|0
N1|N2|N3|N4|N5|N6|N7|N8|N9|N0

S
S+N
S
S
+
+
N
N
Can u make
another parsing
tree ?
5
N
3
2
Dr. Hussien M. Sharaf
17

18. Ex 2
Deduce CFG of a
addition/multiplication and parse the
following expression 2+3*5
 1] S→S+S|S S|N
*
 2] N→1|2|3|4|5|6|7|8|9|0|NN

S
S*S
S
S
+
*
N
N
Can u make
another parsing
tree ?
5
N
3
2
Dr. Hussien M. Sharaf
18

19. Ex 3 CFG without ambiguity

Deduce CFG of a addition/multiplication
and parse the following expression 2*3+5
1] S→ Term|Term + S
2] Term → N|N * Term
3] N→1|2|3|4|5|6|7|8|9|0
S
S+N
S
S
*
+
N
N
Can you make
another parsing
tree ?
5
N
3
2
Dr. Hussien M. Sharaf
19

20. Example 4 : AABB
S
A|AB
A
Λ| a | A b | A A
B
b|bc|Bc|bB
Sample derivations:
S AB AAB
aAB aaB aabB
aabb
S AB AbB
Aabb aabb
A
A
B
A
b
a
B
A
b
a
Dr. Hussien M. Sharaf
B
A
A
a
AAbb
S
S
A
Abb
a
b
b
20

21. Ex 5
S
A
B
A|AB
Λ|a|Ab|AA
b|bc|Bc|bB
S
A
S
B
A
A A b B
a a
S
b
A
a
A
B
A
A b
a
b
A
A A
a
A
A
b
A b
a
Dr. Hussien M. Sharaf
21

22. REMOVING AMBIGUITY
Eliminate “useless” variables.
Eliminate Λ-productions: A Λ.
Avoid left recursion by replacing it with
right-recursion.
But if a language is ambiguous, it can’t be
totally removed. We just need to the
parsing to continue without entering an
infinite loop.
Dr. Hussien M. Sharaf
22

23. THANK YOU
Dr. Hussien M. Sharaf
23