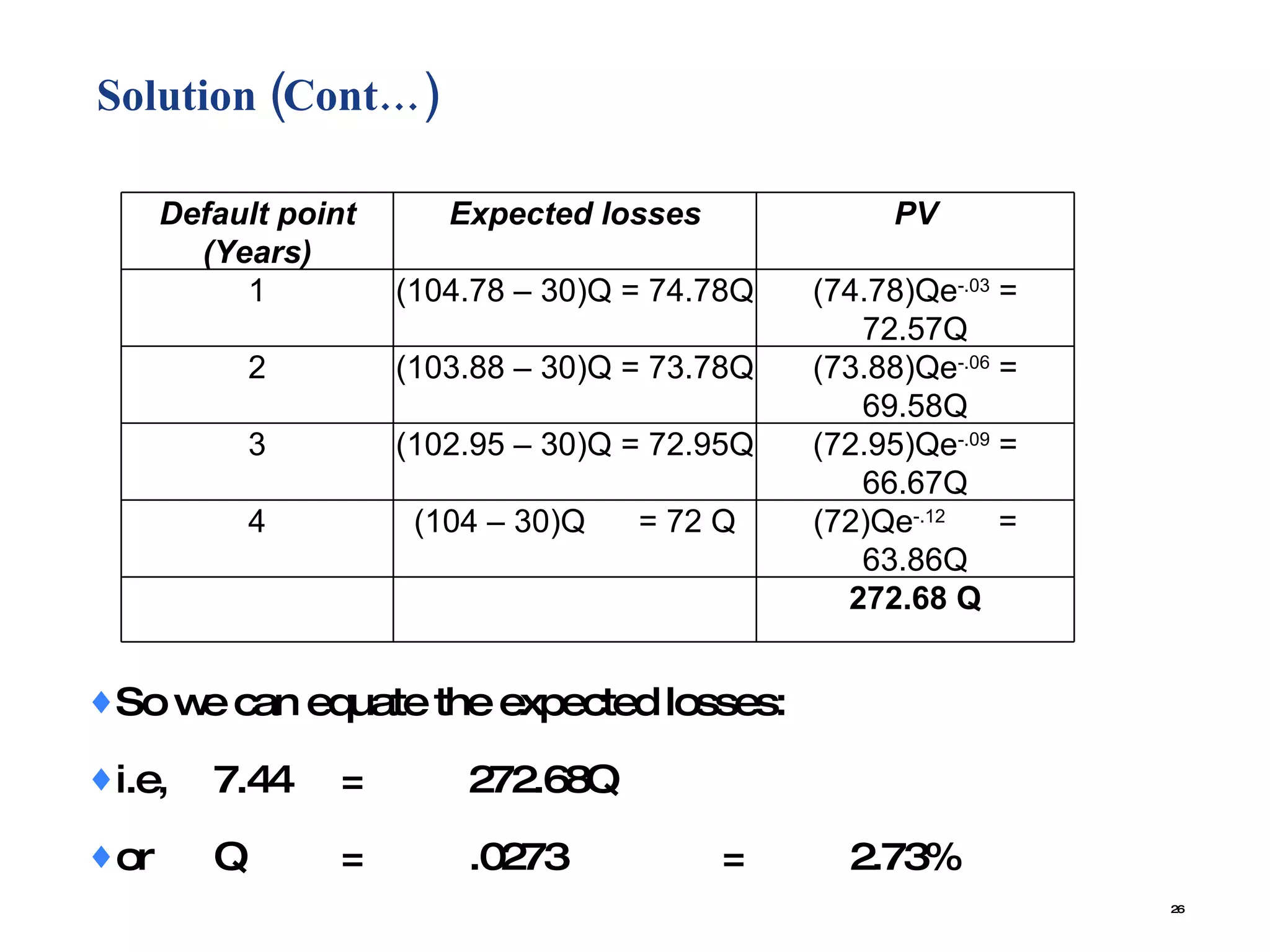
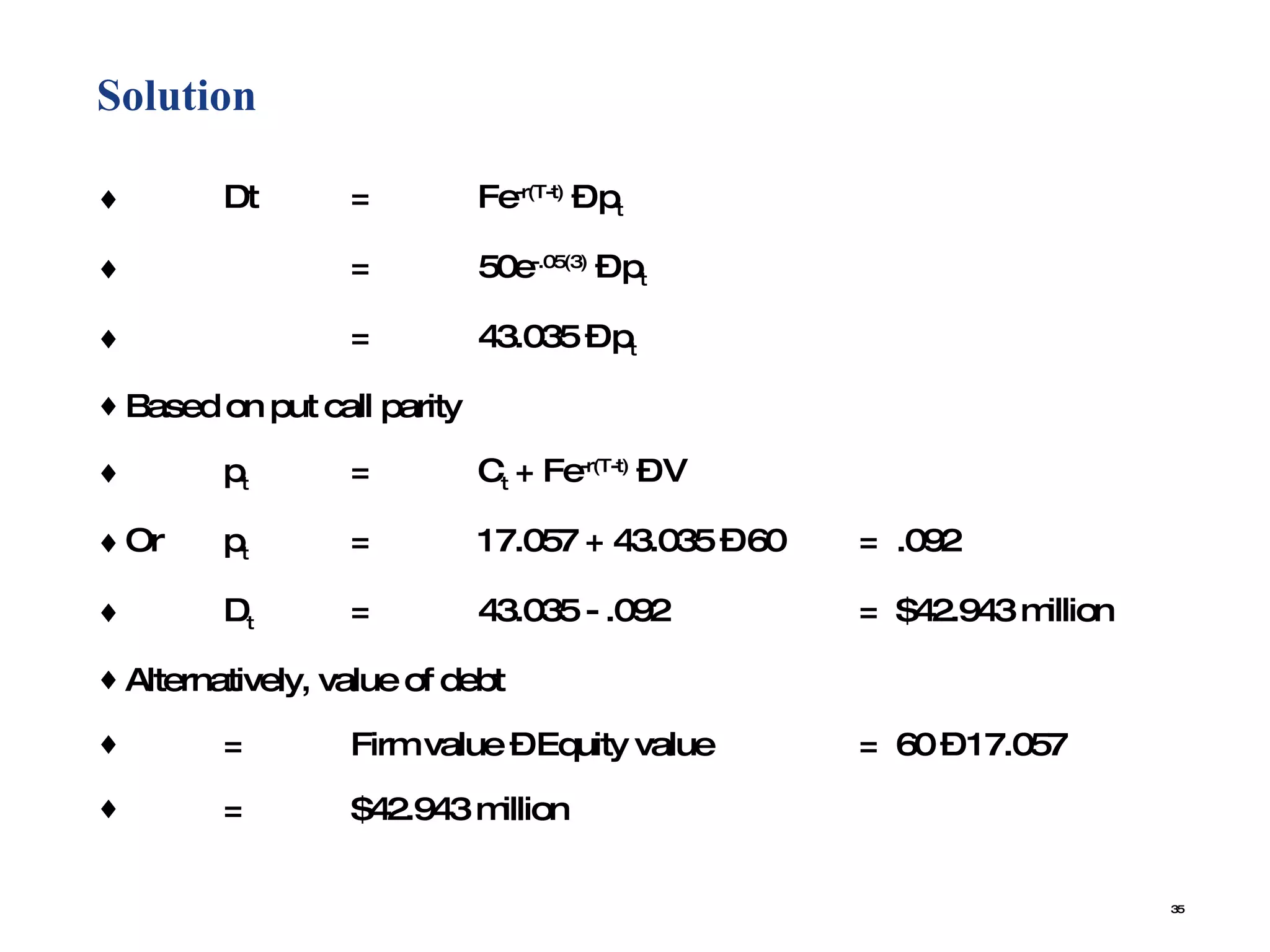
The document contains examples of calculating probabilities of default for bonds and credit portfolios using various inputs like probability of default, loss given default, recovery rates, bond yields, risk free rates, and firm value volatility. The key calculations shown include probability of 1, 2, or more bonds defaulting in a portfolio; cumulative default probability over multiple periods; implied default probability from bond-Treasury yield spreads; and default probability estimation using Merton model inputs like firm value, debt, and equity volatility.




















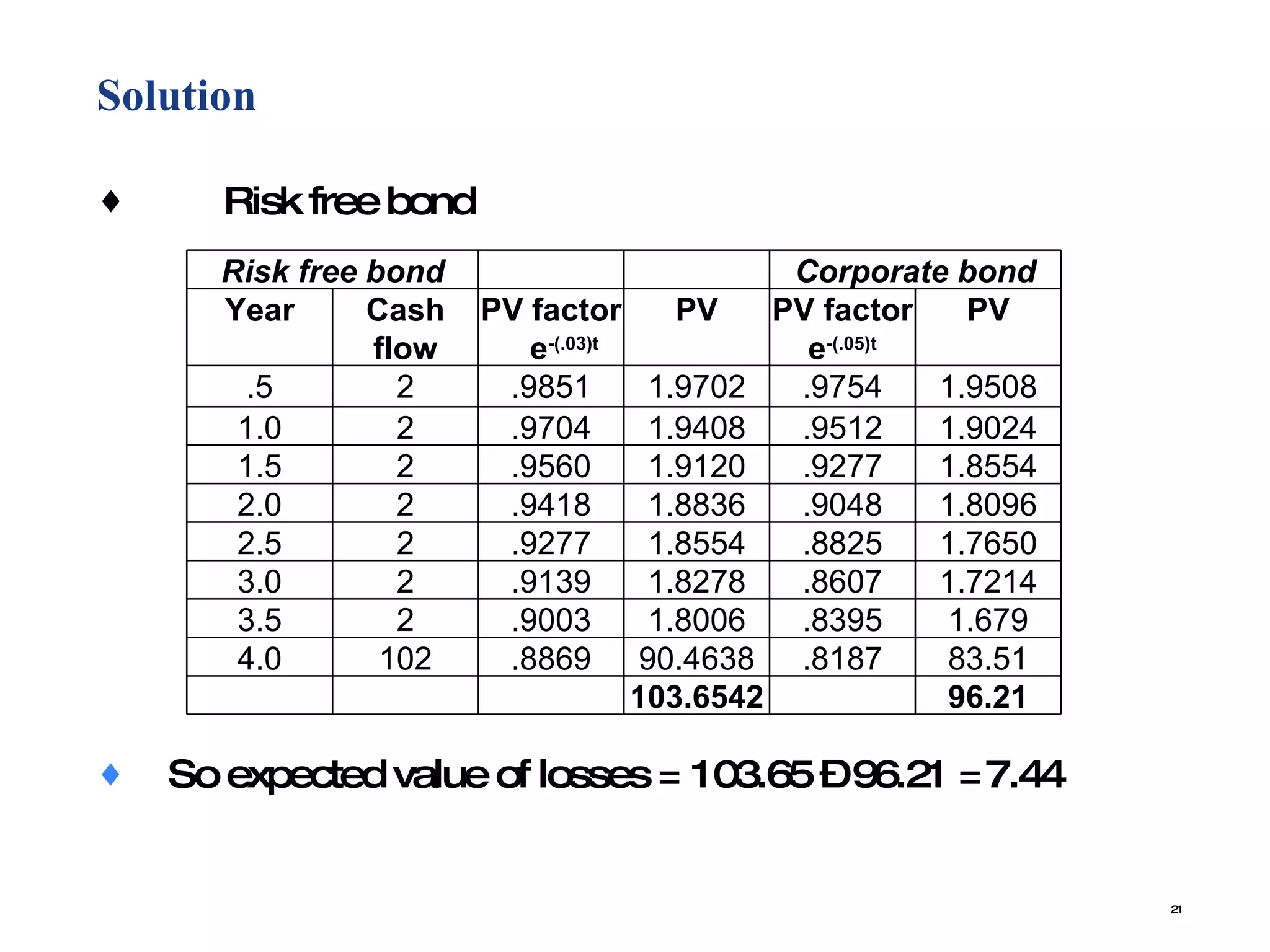


![Solution (Cont…) Time of default = 1 PV of risk free bond = 2+2e -.015 +2e -.030 +2e -.045 + 2e -.060 +2e -075 + (102)e -.090 = 2[1+.9851+.9704+.9560+.9417+.9277]+(102)(.9139) = 11.56 + 93.22 = 104.78 Time of default = 2 PV of risk free bond = 2[1+.9851+.9704 +.9560]+(102) (.9417) = 7.823 + 96.05 = 103.88](https://image.slidesharecdn.com/creditriskmanagementproblems-100103002810-phpapp01/75/Credit-Risk-Management-Problems-24-2048.jpg)
![Solution (Cont…) Time of default = 3 PV of risk free bond = [1+ .9851] + (102) (.9704) = 3.97 + 98.98 = 102.95 Time of default = 4 PV of risk free bond = 102](https://image.slidesharecdn.com/creditriskmanagementproblems-100103002810-phpapp01/75/Credit-Risk-Management-Problems-25-2048.jpg)