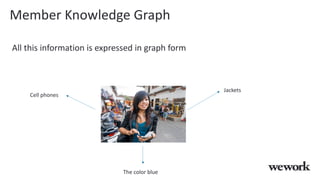
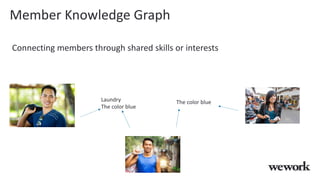
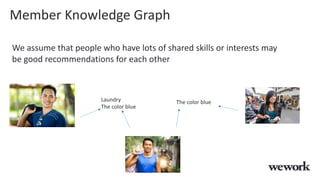
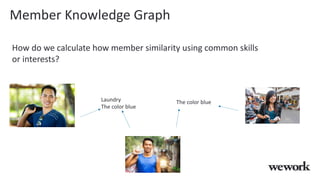
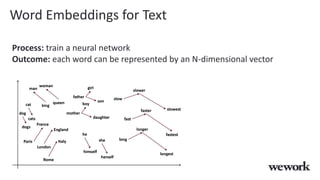
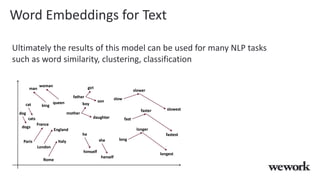
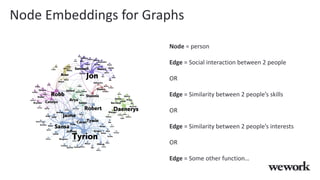
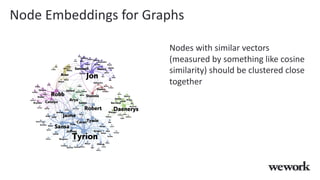
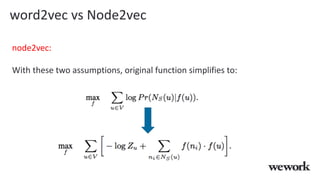
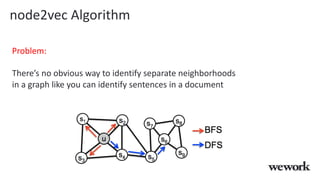
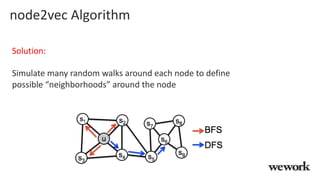
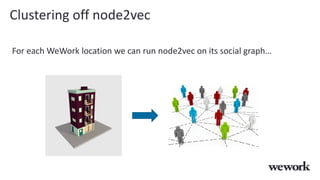
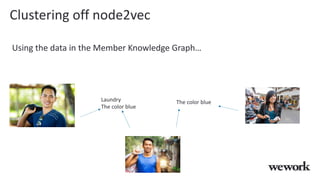
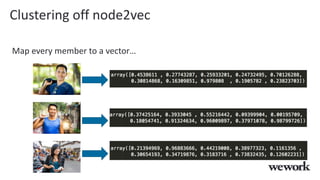
This document discusses how WeWork is using graph embeddings and the node2vec algorithm to power member recommendations. It first describes WeWork's member knowledge graph that contains data on members' profiles, interactions, interests and skills. It then explains how node2vec can learn vector representations of each member node that capture similarities, which can be used for recommendations. WeWork runs node2vec on the social graph of each location to map members to vectors and identify the most similar members to power recommendations like onboarding suggestions and introductions between members.