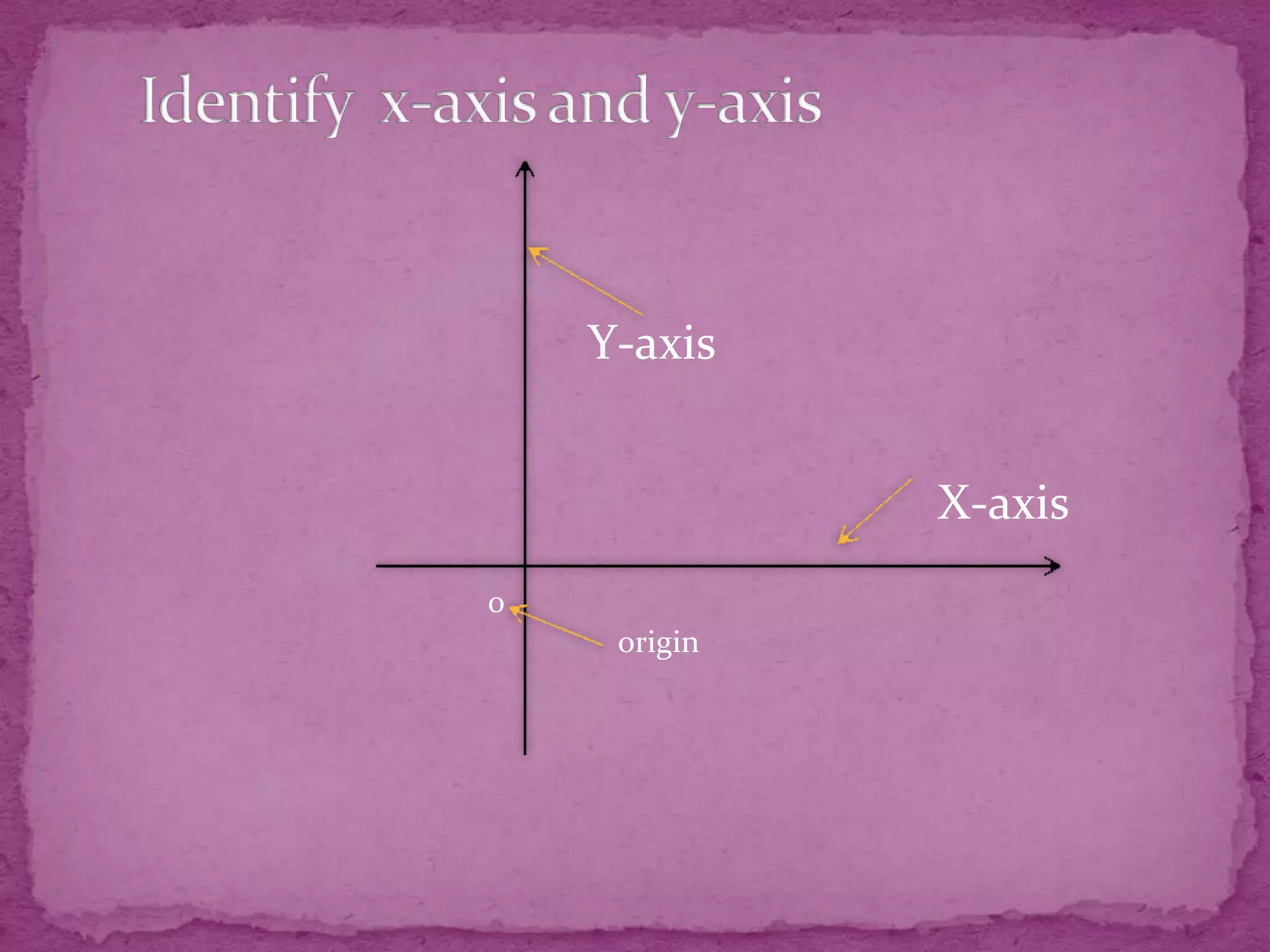
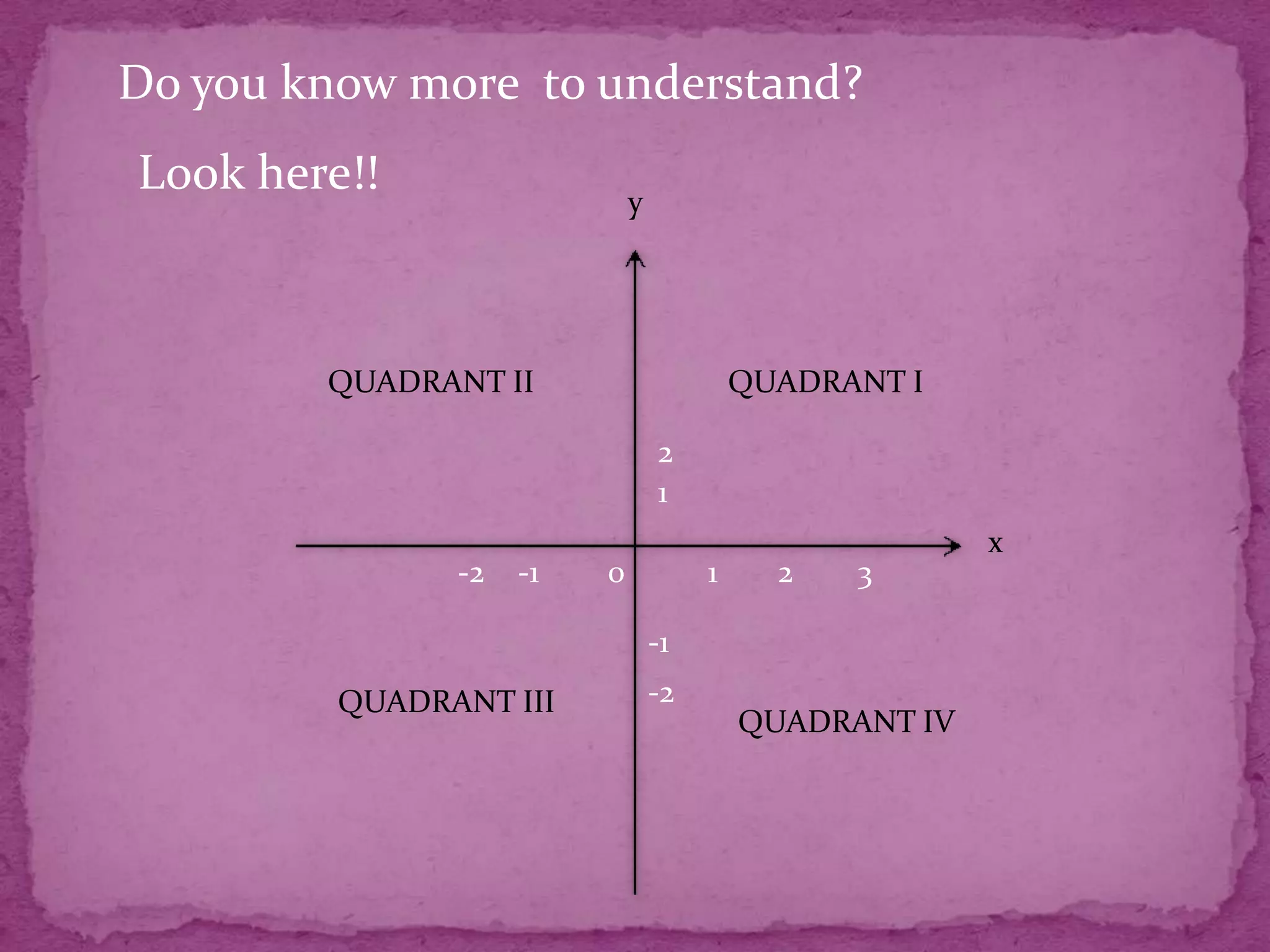
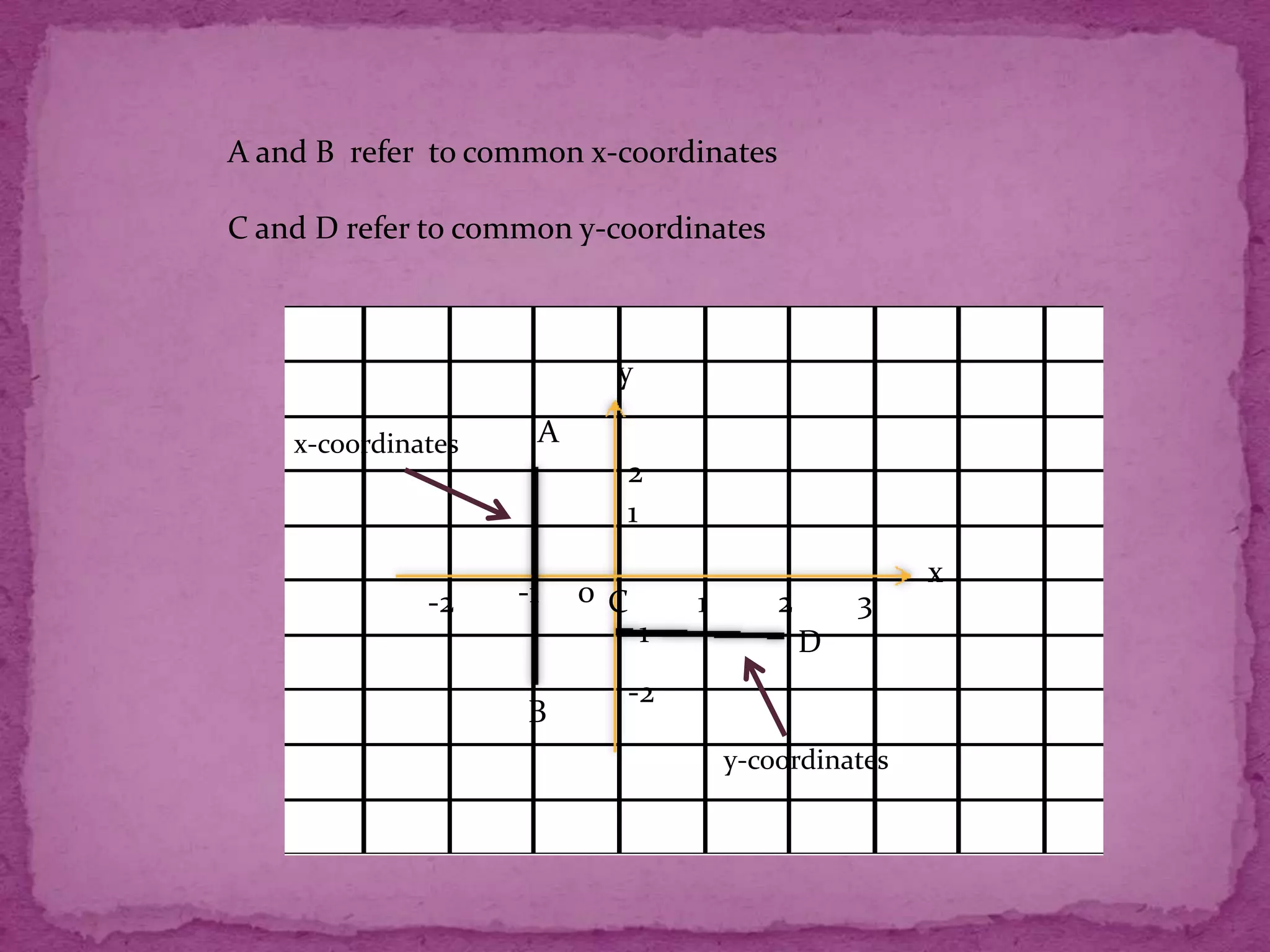
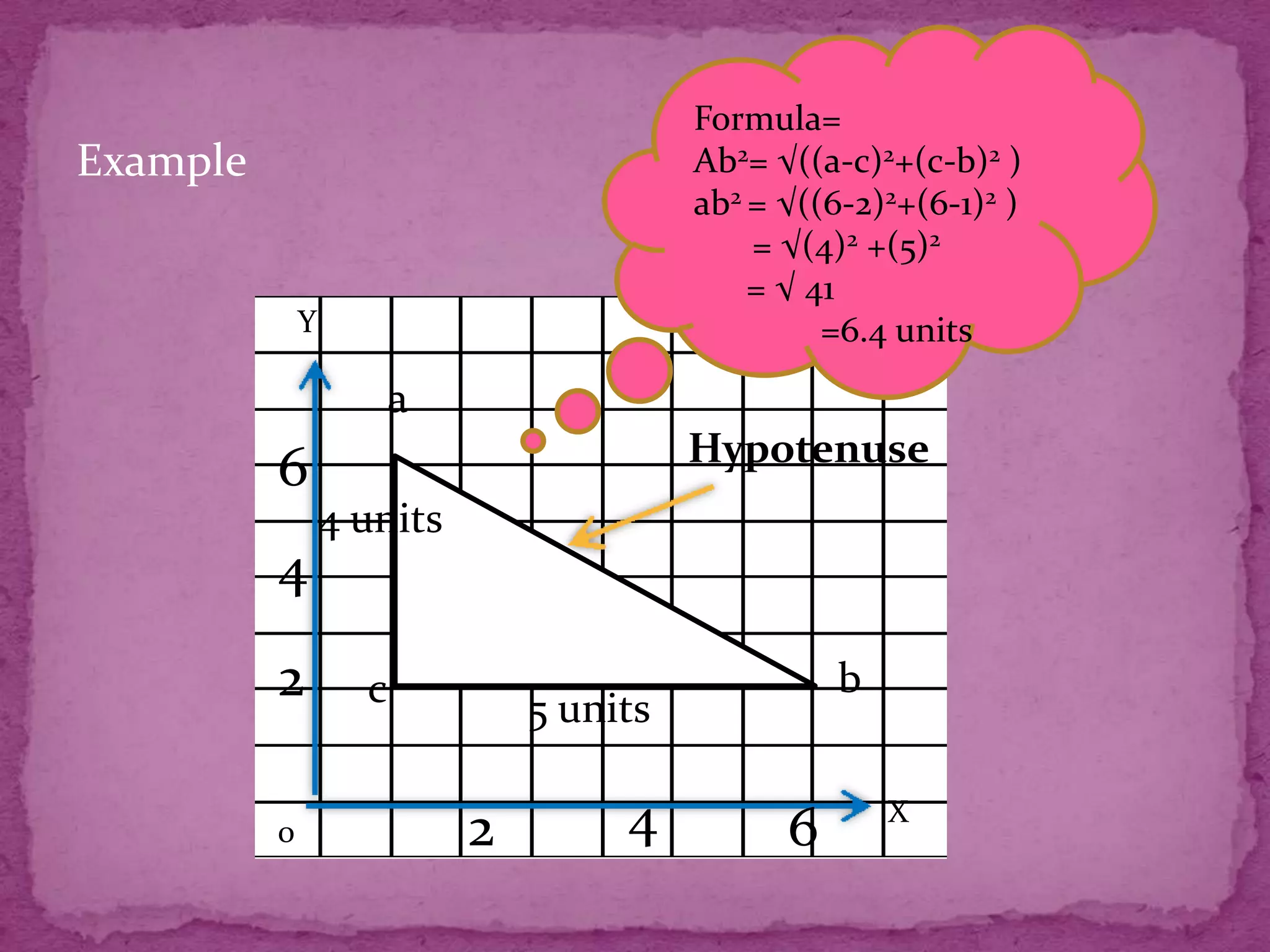
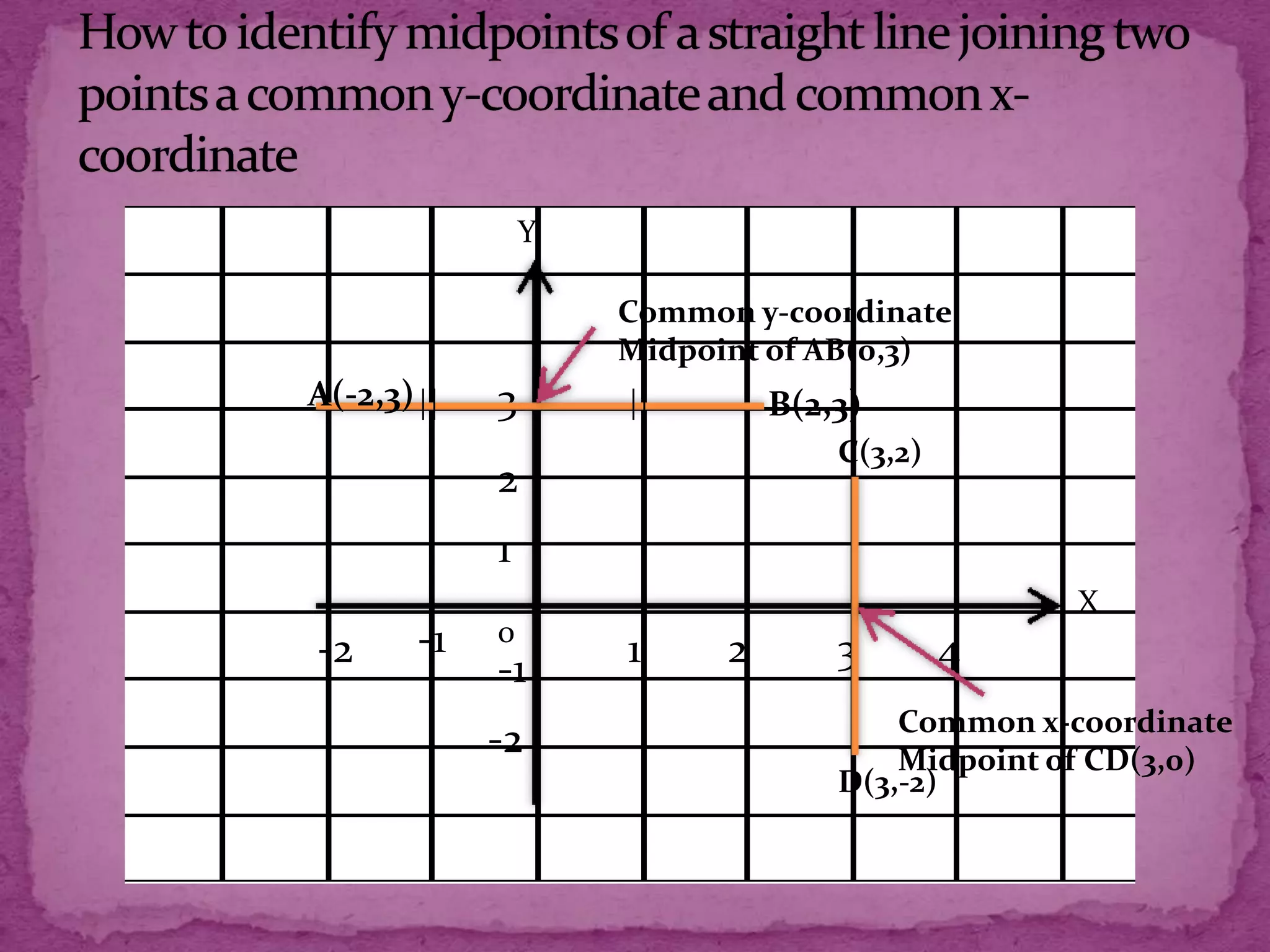
This document provides information about plotting points and calculating distances on a Cartesian plane. It discusses the four quadrants and their definitions. It then explains how to plot points based on their x- and y-coordinates. The document outlines different methods for calculating distances between points, whether they share x- or y-coordinates or not. It also introduces the concept of midpoints and provides examples of finding midpoints between two points.

1. CREATED BY
NURUL HIDAYAH BT MOHAMAD NOR
NURUL KHALISA BT MOHAMED
NURUL SYAKILA BT AHMAD JAILANI
SITI WAN ZULAIKA BT WAN ABD RAHMAN

2. Y-axis
X-axis
0
origin

3. Before draw the scale we should know about four
quadrant.
This is quadrant I, quadrant II, quadrant III and
quadrant I V.
Quadrant I refer to positive (+) where the x-axis
and y-axis is positive.
 Quadrant II refer to negative and positive where
the x-axis is negative and y-axis is positive.
Quadrant III refer to negative(-) where the x-axis
and y-axis is negative.
Quadrant IV refer to positive and negative where
the x-axis is positive and y-axis is negative.

4. Do you know more to understand?
Look here!!
y
QUADRANT II
QUADRANT I
2
1
-2
-1
0
1
2
3
-1
QUADRANT III
-2
QUADRANT IV
x

5.  Every scale has desided in question
 Example:
Mark the values on the x-axis and the y-axis on a
Cartesian plane if the scale for the x-axis
is 1 : 2
and the scale for the y-axis is 1 : 5.
 1 unit(1 cm in
graph paper) on the x-axis
represents 2 units
 1 unit (1 cm in graph paper) on the y-axis
represents 5 units .

6. y
15
10
5
-6 -4
-2 0
2
-5
-10
-15
4
6
8
10
X

7. How to student plot the point?
 Start read the point by x-axis
For example:
A(4,-1) =4 for x-axis and -1 for y-axis
y
2
1
-1
0
1
-1
-2
2
3
4
x
A(4,-1)

8.  The distance between two points is the length of the
straight line which joins the two points.
Find the distance two point?
i.
Points with common y-coordinates .
The straight line which joins two points that have the
same y-coordinates is parallel to the x-axis. Therefore,
the distance between two points, with common ycoordinates is the difference between their xcoordinates.
ii. Points with common x-coordinates
The straight line which joins two points that have the
same x-coordinates is parallel to the y-axis. Therefore,
the distance between two points with common xcoordinates is the difference between their ycoordinates.

9. A and B refer to common x-coordinates
C and D refer to common y-coordinates
y
x-coordinates
-2
A
2
1
-1
B
0 C
-1
1
2
3
D
-2
y-coordinates
x

10. How to calculate the distance?
Common x-coordinates
Distance between A and B
=2-(2)
=2+2
=4 units
Common y-coordinates
Distance between C and D
=2-(-1)
=2+1
=3 units
Please read at y-axis
to calculate common
x-coordinate
Please read at y-axis
to calculate common
x-coordinate

11.  The
distance between any two points with
different x-coordinates and y-coordinates is the
length of the straight line joining the two points.
 The straight line is the hypotenuse of a rightangled triangle where its two other sides
are parallel to the x-axis and y-axis respectively.
a
Formula=
ab2= √(a-c)2+(c-b)2
c
b

12. Formula=
Ab2= √((a-c)2+(c-b)2 )
ab2 = √((6-2)2+(6-1)2 )
= √(4)2 +(5)2
= √ 41
=6.4 units
Example
Y
a
Hypotenuse
6
4 units
4
2
0
c
b
5 units
2
4
6
X

13. Identify the midpoints of straight lines
 The midpoint of a line joining two points is the point that
divides the line into two equal parts
a
||
x
||
b
midpoint

14. Y
Common y-coordinate
Midpoint of AB(0,3)
A(-2,3) ||
3
||
B(2,3)
C(3,2)
2
1
-2
-1
0
-1
-2
X
1
2
3
4
Common x-coordinate
Midpoint of CD(3,0)
D(3,-2)

15.  Example
 Common y-coordination
 Find the coordination of the midpoint of a line joining
point A(-2,3) and B(2,3).
 Solution
 X-coordinate for the midpoint = (-2+2)/2
= 0/2
=0
Y-coordinate for the midpoint=3
Therefore, the midpoint for the line AB
is(0,3)

16.  Example
 Common x-coordinate
 Find the coordination of the midpoint of a line joining
point C(3,2) and D(3,-2).
 Solution
 y-coordinate for the midpoint = (2+(-2))/2
= 0/2
=0
x-coordinate for the midpoint=3
Therefore, the midpoint for the line AB
is(3,0)

17. Midpoint = sum of x-coordinates , sum of y-coordinates
2
2
Can use this formula when
coordinate at x-coordinate and
y-coordinate is not same

18.  Example
 Find the coordinates of the midpoint of the line
joining S(3,1) T1,-5).
 Solution
 X-coordinate of the midpoint
 = 3+1/2
=4/2
=2
Y-coordinate of the midpoint
=1-(-5)/2
=6/2
=3
Therefore, the coordinates of the midpoint of line ST
are(2,3)

19. Thank you