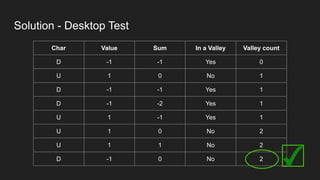
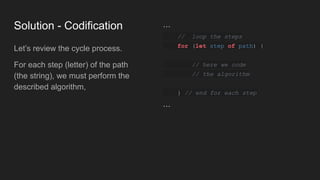
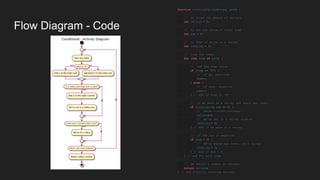
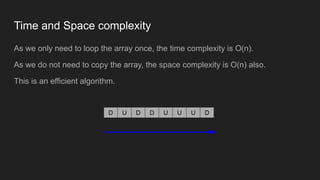
The document describes a programming problem from HackerRank involving counting valleys based on movements represented by 'u' for up and 'd' for down. It outlines an algorithm using an array to track movements, where valleys are counted when the sum of movements is negative and returns to zero. The solution is implemented in JavaScript, with emphasized best practices for writing clear, readable code and performing comprehensive testing.

1. Counting Valleys
Programming problem in hackerrank.com

2. Description
Imagine a straight line, a sea level.
If we go Up, we’re above the sea
level, in a hill.
While there, if we go down, we got to
sea level again.
If we go down again, we’re below sea
level, in a valley.
If we go up again, we’re again at sea
level.
Start
Up
Down
Down
Up

3. Description
Problem is the following: Given a series of movements, represented by a string, in
which “U” means “go Up” and “D” means “go Down”, count all the times we’re
below sea level, in a valley.
For example: DUDDUUUD
Meaning: Down, Up, Down, Down, Up, Up, Up, Down
1
2
The number of valleys is 2

4. Solution - Data Structure
First thing is to determined which data structure we need.
As we view in the graphical representation, we can count the valleys in a linear
way, by an iteration of every command (Up or Down).
So the data structure we need is an array. A string is an array of characters.
D U D D U U U D

5. Solution - Algorithm
Next to define is the steps we’re going to perform.
- To solve the problem, we need to know when we’re down the sea level, and
when we reach sea level again.
- Easiest way is assign a value to up’s and downs, 1 and -1, and sum them on
every iteration.
- If the sum is smaller than 0 (negative), we’re in a valley.
- We should count the valley once we reach sea level again, when sum is equal
to zero once more time.
Now, let’s put our algorithm to test.

6. Solution - Desktop Test
Char Value Sum In a Valley Valley count
D -1 -1 Yes 0
U 1 0 No 1
D -1 -1 Yes 1
D -1 -2 Yes 1
U 1 -1 Yes 1
U 1 0 No 2
U 1 1 No 2
D -1 0 No 2

7. Solution - Codification
Once our algorithm is validated, then
we can code it with confidence.
The language used here is Javascript.
Good practices is write the algorithm in
comments, to describe what the
program is doing.
We can easily follow the commented
code to review the algorithm.
function countingValleys
(steps, path) {
// to store the amount of valleys
let valleys = 0;
// to sum the value of every step
let sum = 0;
// to know if we're on a valley
let inValley = 0;
// loop the steps
for (let step of path) {
// add the step value
if (step == 'U') {
// if up, positive
sum++;
} else {
// if down, negative
sum--;
} // end if step is 'U'
// if we were on a valley and reach sea level
if (inValley && sum == 0) {
// value counter increase
valleys
++;
// we're not in a valley anymore
inValley = 0;
} // end if we were in a valley
// if the sum is negative
if (sum < 0) {
// we're below sea level, in a valley
inValley = 1;
} // end if sum < 0
} // end for each step
// we return a number of valleys
return valleys
;
} // end function counting valleys

8. Solution - Codification
First thing we got to do is to get
the signature right, meaning the
parameters and the output are
setup correctly.
/**
* We receive a number of steps
* and a string representing a path
*/
function countingValleys(steps, path) {
// we return a number of valleys
return valleys;
} // end function counting valleys

9. Solution - Codification
As we’re starting with algorithms
and data structures, a good
practice is to declare all variable
we’re gonna need and give them
descriptive names.
Also, it will be easier for the the
person reading the code to follow
the algorithm.
...
// to store the amount of valleys
let valleys = 0;
// to sum the value of every step
let sum = 0;
// to know if we're on a valley
let inValley = 0;
...

10. Solution - Codification
Now we implement the validated
algorithm.
Code can be pretty short and
concise, nevertheless the example
here is verbose for clarification
purposes.
Readability and clarity are key
whenever you’re learning or
reviewing a piece of code.
You can always refactor it to make it
neat and simple.
...
// loop the steps
for (let step of path) {
// add the step value
if (step == 'U') {
// if up, positive
sum++;
} else {
// if down, negative
sum--;
} // end if step is 'U'
// if we were on a valley and reach sea level
if (inValley && sum == 0) {
// value counter increase
valleys++;
// we're not in a valley anymore
inValley = 0;
} // end if we were in a valley
// if the sum is negative
if (sum < 0) {
// we're below sea level, in a valley
inValley = 1;
} // end if sum < 0
} // end for each step
...

11. Solution - Codification
Let’s review the cycle process.
For each step (letter) of the path
(the string), we must perform the
described algorithm,
...
// loop the steps
for (let step of path) {
// here we code
// the algorithm
} // end for each step
...

12. Solution - Codification
Inside the loop, first thing we’re
gonna need is determine the
movement.
If ‘Up’, add one unit to the total
sum, otherwise (is ‘Down’),
subtract one unit.
...
// add the step value
if (step == 'U') {
// if up, positive
sum++;
} else {
// if down, negative
sum--;
} // end if step is 'U'
...

13. Solution - Codification
Next step is search if we must add
any valleys.
To do this, apply the condition:
- If we were in a valley, and
now we’re again at sea level,
add a valley to the counter.
- As we reach sea level, now
we’re not in a valley.
...
// if we were on a valley
// and reach sea level
if (inValley && sum == 0) {
// value counter increase
valleys++;
// we're not
// in a valley anymore
inValley = 0;
} // end if we were in a valley
...

14. Solution - Codification
Finally, if the total sum of values
for the positions (up’s and down’s)
is negative, we’re in a valley.
And with this we’ve finished
implemented the algorithm for the
iteration.
After cycle ends, program return
the counter of valleys.
Let’s view a diagram of our
solution.
...
// if the sum is negative
if (sum < 0) {
// we're below
// sea level
// in a valley
inValley = 1;
} // end if sum < 0
...

15. Flow Diagram - Code
function countingValleys
(steps, path) {
// to store the amount of valleys
let valleys = 0;
// to sum the value of every step
let sum = 0;
// to know if we're on a valley
let inValley = 0;
// loop the steps
for (let step of path) {
// add the step value
if (step == 'U') {
// if up, positive
sum++;
} else {
// if down, negative
sum--;
} // end if step is 'U'
// if we were on a valley and reach sea level
if (inValley && sum == 0) {
// value counter increase
valleys
++;
// we're not in a valley anymore
inValley = 0;
} // end if we were in a valley
// if the sum is negative
if (sum < 0) {
// we're below sea level, in a valley
inValley = 1;
} // end if sum < 0
} // end for each step
// we return a number of valleys
return valleys
;
} // end function counting valleys

16. Time and Space complexity
As we only need to loop the array once, the time complexity is O(n).
As we do not need to copy the array, the space complexity is O(n) also.
This is an efficient algorithm.
D U D D U U U D

17. Test the solution
Our algorithm most run for a variety of cases:
- Plain straight, happy path cases.
- Edge cases (very short of very large).
- Empty of null cases (what if no input is provided).
- Time execution and memory allocation.
- Must perform in a short amount of time and with as little resources as possible.
We need to know the answer beforehand in order to be able to test it.
There’s a myriad of testing tools, or we can simple code a test function that
evaluates the code and check against a pre-defined answer.

18. Key Takeaways
- Understand and create a clear image of the problem in your mind.
- Draw it helps a lot.
- Determine the data structure to use is solve the half of the problem.
- Write the algorithm steps and perform a desktop test to validate it before
writing the code.
- Write clear and readable code, with comments about what the program is
doing.
- Perform tests for major categories of problems, short, long, straight-forward,
special cases.

19. Thank you.
@espino316
allmylinks.com/luisespino