I am Kepha M. I am a Control System Assignment Expert at matlabassignmentexperts.com. I hold a Ph.D. in Matlab, McGill University, Canada. I have been helping students with their homework for the past 8 years. I solve assignments related to Control Systems. Visit matlabassignmentexperts.com or email info@matlabassignmentexperts.com. You can also call on +1 678 648 4277 for any assistance with Control System Assignments.

1. Dynamics and Control
For Any Quarries or info, Contact us on :- +1 678 648 4277
You can Mail us on :- info@matlabassignmentexperts.com
Visit us on :- https://www.matlabassignmentexperts.com/
Matlab Assignment Help

2. Problem 1 : Calculating the factorial of non-negative integer with recursion
Write a function to calculate the factorial of non-negative integer, n! as in the last homework.
However, for this time, you should use a recursive algorithm. Function name (and m-file name)
should be ‘fctrlrc_your_kerberos_name’ and upload it to 2.003 MIT Server site. You also
submit hardcopy of your code. Calculate 125! with this function.
Solution:
Calculating the factorial of non-negative integer with recursion
n! is associated with (n −1)! as below:
n! = nx(n-1)x….x2x1=nx(n-1)!
Therefore, the function of calculating n! is achieved by calling itself for (n-1)! and multiplying n
. m-file is shown as below:
Matlab Assignment Help

3. The output of 125! will be displayed as below.
Matlab Assignment Help

4. Problem 2 : Developing the Algorithm for the Solution of the Tower of Hanoi
The tower of Hanoi (commonly also known as the "towers of Hanoi"), is a mathematical
game or puzzle invented by E. Lucas in 1883. It is also very famous example for using
recursion in programming. It consists of three posts, and N different size disks. Initially, N
disks are stacked on the leftmost side post (starting post or post 1) in the order of the largest
one on the bottom to the smallest one on the top. Your task is to move all the disks on the
rightmost side post (end post or post 3) with same order of disks. You can use the middle
post (intermediate post or post 2) for temporary stacking of disks.
During the movement of disks, you must further follow these rules:
1. Only one disk is allowed to be moved at a time.
2. In each move, only the disk on the top of any post can move and be
stacked on another post.
3. The bigger disk must always be stacked below the smaller ones.
Matlab Assignment Help

5. i) Obtain the solution for the tower of Hanoi with N=2 different size disks. Don’t try to use
MATLAB at this time. Just write down the order of disk movements as below:
‘Trial number’ : from ‘post number’ to ‘post number’
ii) Express your algorithm for the solution of the tower of Hanoi with N different size disks. You
can assume that you have the algorithm for solving the N-1 disk problem. You can then develop
an algorithm for the N-disk problem using the N-1 disk solution based on recursive.
Solution:
Developing the Algorithm for the Solution of the Tower of Hanoi
i) Now, you have 2 different size disks, the small and the big one, in the tower of Hanoi.
First, top disk (the small one) on the starting post can be moved to either intermediate
post or ending post. Since ending post should be reserved for the big disk, the small one
is moved to intermediate post (from 1 to 2). Next, remaining disk (the big one) on the
staring post should be stacked on the ending post since there is no disk on this post.
(from 1 to 3). Finally, the disk placed on the intermediate post is also stacked on the
ending post.
1: from 1 to 2
2: from 1 to 3
3: from 2 to 3
Matlab Assignment Help

6. ii) Assume that you have N different size disks for the tower of Hanoi. They are located on
the starting post. Now, we define function MoveTower(N,sp,ep,ip) to move whole N disks
from the starting post (sp) to ending post (ep) with using intermediate disk (ip). This function
can be rewritten with MoveTower associated with (N-1) disks movement.
To move whole disks from one to another, at least the biggest disk should move from sp to
ep. To achieve this task, (N-1) disks on top of the biggest should move from spto ip at first.
After moving the biggest disk, (N-1) disk on the intermediate post (ip) should be stacked to
the ending post (ep). This procedure for recursive algorithm is also described in below
figures.
In addition to general case, special case N=0 should be considered. Since
MoveTower(0,sp,ep,ip) means that there is no disk to move, nothing will be done.
Therefore, following description is for the recursive algorithm for the solution of the
tower of Hanoi with N different size disks
Matlab Assignment Help

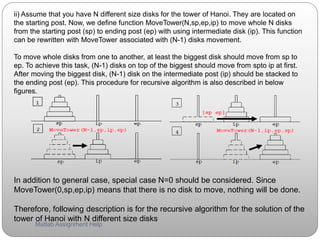
7. 1. If N is smaller than 1, just return (in the special case of MoveTower(0,sp,ep,ip))
2. Output Å MoveTower(N-1,sp,ip,ep) (move N-1 disks from sp to ip)
3. Output Å [sp ep] (move the biggest disk from sp to ep)
4. Output Å MoveTower(N-1,ip,ep,sp) (move N-1 disks from ip to ep)
Matlab Assignment Help

8. Problem 3 : Solving the Tower of Hanoi with recursive algorithm
Now, generate the function or m-file for the solution of “tower of Hanoi” with 5 different size
disks. Use recursive approach. Your function has input argument of ‘n’, number of disk on the
starting post, and output argument of ‘o’, matrix for disk movements (each row represents each
movement from the post indicated in the first column to the post shown in the second column.
For example, [1 3] means movement from post 1 to post 3) Function name (and m-file name)
should be ‘hanoi_your_kerberos_name’ and upload it to 2.003 MIT Server site. You submit
hardcopy of your function code as well as the solution of the tower of Hanoi with 5 different size
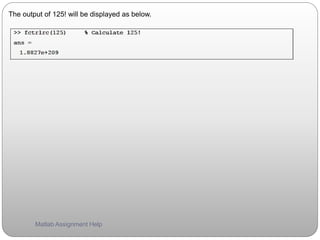
disks. Execution of m-file should provide the following result in case of N=1:
Solution:
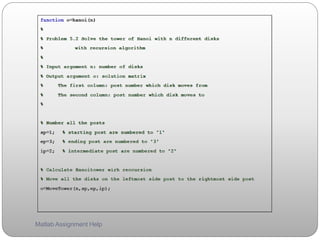
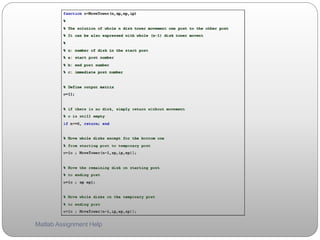
By using your own algorithm, the function to solve the tower of Hanoi is shown as below.
Please, see the comments for each line.
Matlab Assignment Help

9. Matlab Assignment Help

10. Matlab Assignment Help

11. The solution of the tower of Hanoi with 5 different size disks is represented as below:
Matlab Assignment Help

12. Problem 4 : (Optional) Comparison between solving problem with and without
recursion.
In problem 5.1., you are asked to make the function of calculating n! with different algorithms.
These functions basically work same in terms of mathematics, but they don’t in terms of
computer performance. Describe both advantage and disadvantage of each approach briefly.
Solution:
Two m-code works same in terms of the output of calculating the factorials. However, they are
not quite different in the view of computer and programming performance. First, the program
with the recursive algorithm is very concise, and easy to understand. Recursive algorithm
requires so many function calls, and it needs stack memories to keep current position of
program counter and some variables for each function call. In addition, function call needs
much more . CPU time than normal operations. Eventually, running the code with recursion
gives the value too late where large number of recursion is necessary. In case of
programming without recursion, program itself can be a little complicated, but it runs faster
than recursive version. However, it is sometimes much more useful to solve the problem
recursively than sequentially like the tower of Hanoi.
Matlab Assignment Help