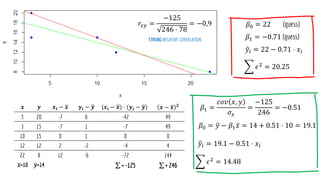
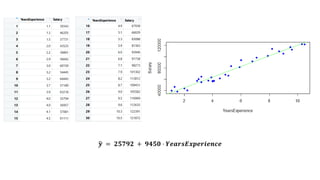
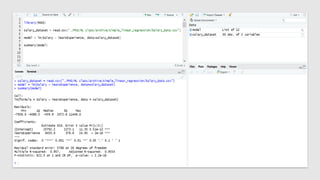
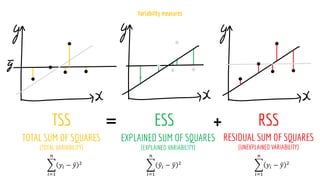
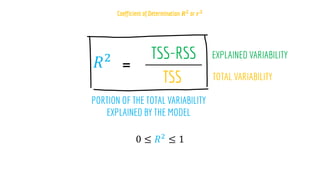
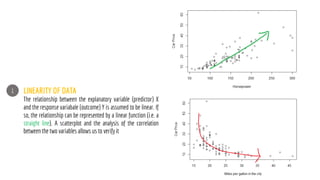
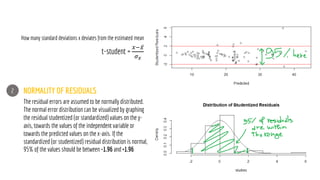
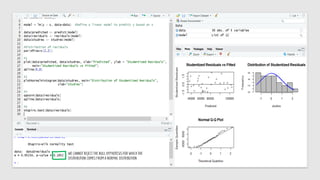
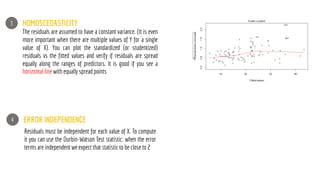
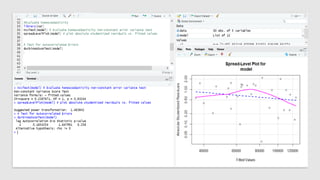
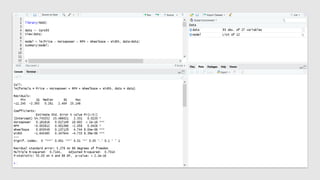
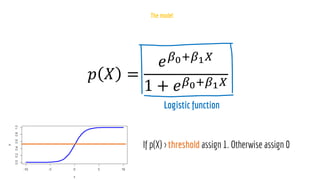
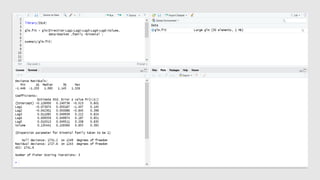
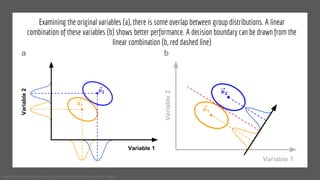
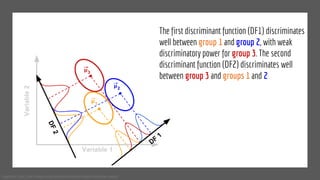
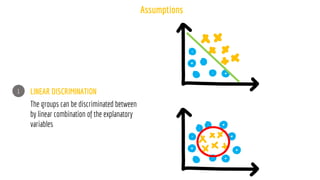
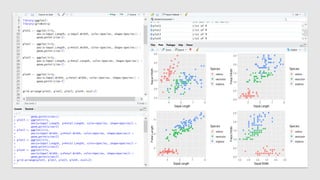
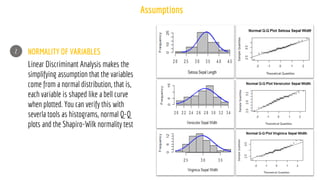
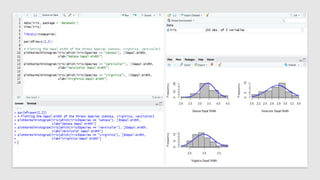
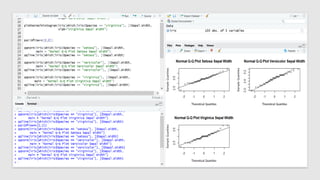
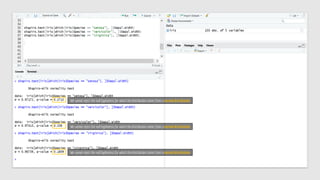
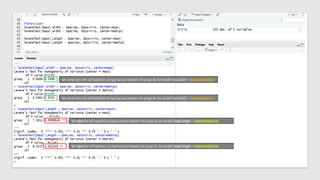
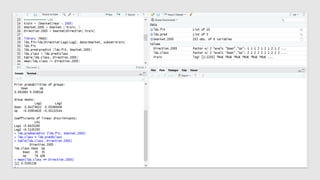
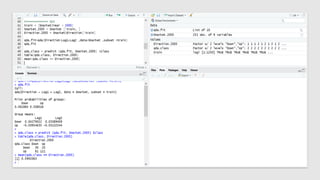
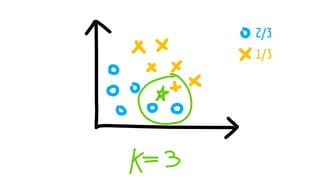
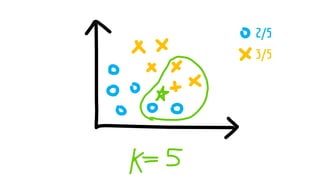
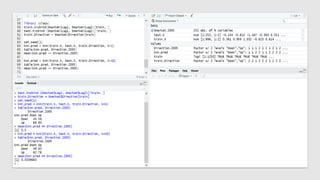
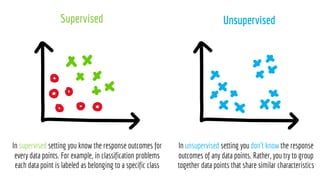
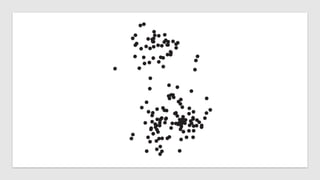
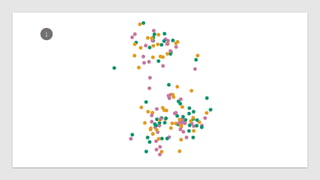
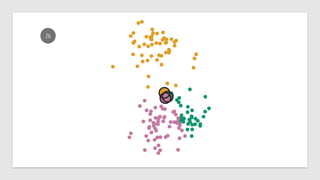
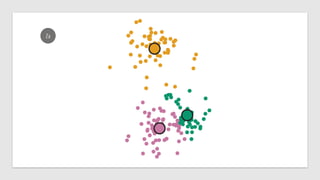
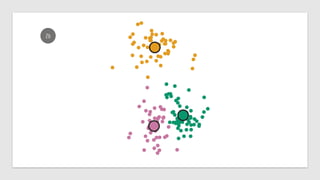
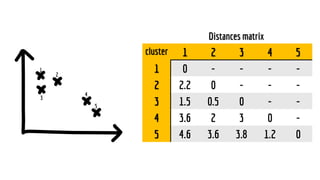
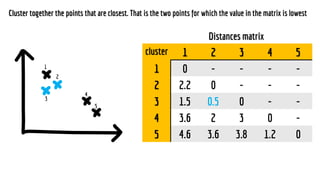
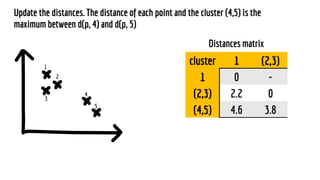
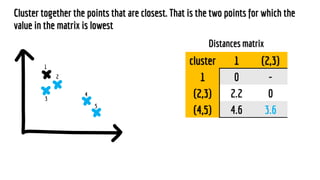
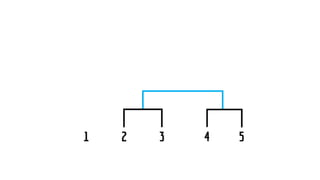
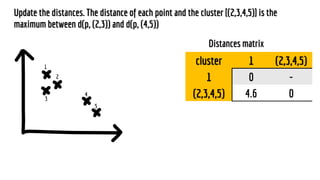
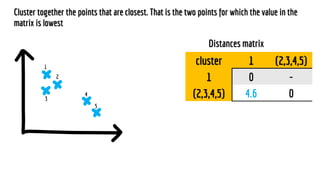
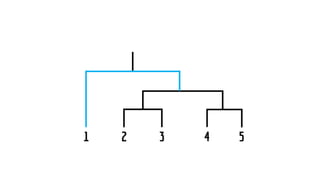
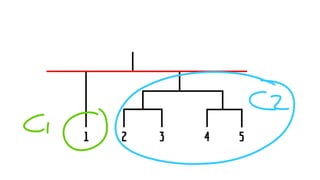
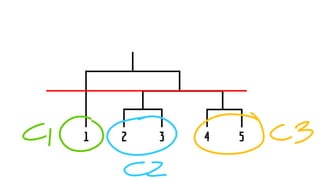
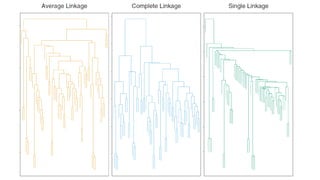
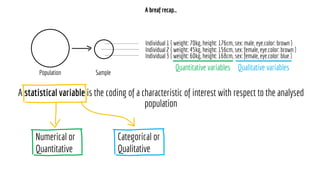
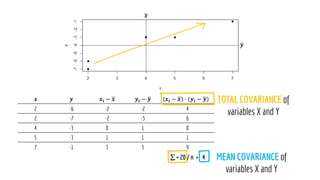
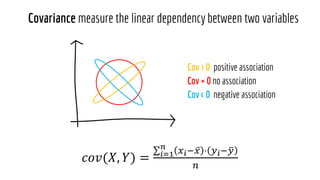
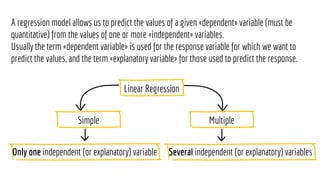
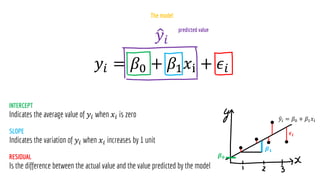
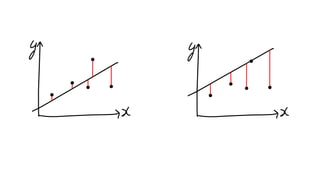
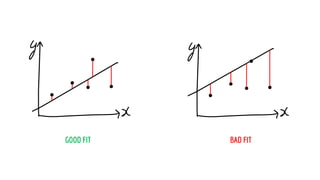
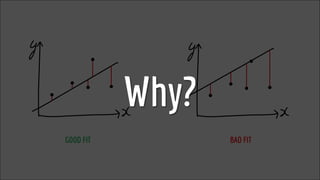
The document discusses statistical concepts including variance, covariance, and regression analysis. It provides formulas for calculating estimates and coefficients, emphasizing the relationship between dependent and independent variables in regression models. Additionally, it highlights the importance of model evaluation metrics, such as R-squared, in assessing model fit.











![𝑦𝑖 ො
𝑦𝑖
𝐚𝐫𝐠 𝒎𝒊𝒏
𝜷𝟎, 𝜷𝟏
𝒊=𝟏
𝒏
𝝐𝒊
𝟐
arg min
𝛽0, 𝛽1
𝑖=1
𝑛
[𝑦𝑖 − (𝛽0 + 𝛽1𝑥𝑖)]2
ො
𝑦𝑖 = 𝛽0 + 𝛽1𝑥𝑖
𝑦𝑖 = ො
𝑦𝑖 + 𝜖𝑖
𝝐𝒊 = 𝒚𝒊 − ෝ
𝒚𝒊
𝜷𝟏 =
𝒄𝒐𝒗 𝒙, 𝒚
𝝈𝒙
𝟐
𝜷𝟎 = ഥ
𝒚 − 𝜷𝟏ഥ
𝒙
⇒](https://image.slidesharecdn.com/introductiontomachinelearningwithexamplesinr-220819103316-5f905112/85/Introduction-to-Machine-Learning-with-examples-in-R-26-320.jpg)