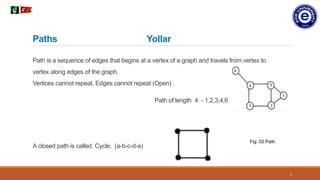
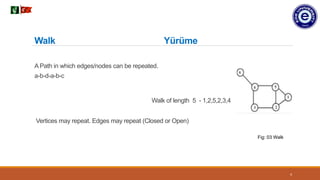
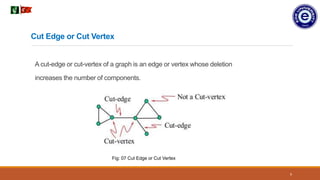
1. Graph theory can be used to model connectivity problems in computer networks. Connectivity refers to whether messages can be sent between any two computers using intermediate links. 2. There are different path types in graphs including simple paths where vertices and edges cannot be repeated, and walks where vertices and edges may be repeated. 3. A computer network is represented by a graph where computers are vertices and communication links are edges. For any two computers to communicate, the graph must be connected - meaning there is a path between any two vertices.

1. Present by: Abdul Ahad Abro
1
Graph Theory in Computer Applications
Computer Engineering Department, Ege University, Turkey
October 26-2017
Connectivity

2. Connectivity Bağlantı
The message can be sent between two computers using intermediate links
can be studied with a graph model. Problems of efficiently planning routes for
mail delivery, garbage pickup, diagnostics in computer networks and so on
can be solved using models that that involve paths in graphs .
2
Fig: 01 Connectivity

3. Path is a sequence of edges that begins at a vertex of a graph and travels from vertex to
vertex along edges of the graph.
Vertices cannot repeat. Edges cannot repeat (Open) .
Path of length 4 - 1,2,3,4,6
A closed path is called Cycle. (a-b-c-d-a)
3
Paths Yollar
Fig: 02 Path

4. A Path in which edges/nodes can be repeated.
a-b-d-a-b-c
Walk of length 5 - 1,2,5,2,3,4
Vertices may repeat. Edges may repeat (Closed or Open)
4
Walk Yürüme
Fig: 03 Walk

5. Trail: iz
If all the edges (but not necessarily all the vertices) of a walk are different, then the walk is
called a trail.
No Edge can be repeat.
a-b-c-d-e-b-d
5
Fig: 04 Trail

6. A circuit is a path that begins and end at the same vertex.
6
In this graph a,d,c,f,e is a simple path of length 4, because {a,d}, {d,c}, {c,f} and {f,e} are all
edges. However d,e,c,a is not a path because {e,c} is not an edge. Where as {b,c}, {c,f}, {f,e}
and {e,b} are edges and this path begins and ends at b.
Circuit
Fig: 05 Simple Graph

7. 7
When does a computer network have the property that every pair of
computers can share information, if messages can be sent through one or
more intermediate computers? When a graph is used to represent this
computer network, where vertices represent the computers and edges
represent the communication links.
Connectedness in Undirected Graphs

8. The graph H and its connected components H1, H2, H3
8
Any two computers in the network can communicate if and only if the graph of this
network is connected .
Fig: 06 Connected Components

9. 9
A cut-edge or cut-vertex of a graph is an edge or vertex whose deletion
increases the number of components.
Cut Edge or Cut Vertex
Fig: 07 Cut Edge or Cut Vertex

10. 10
A directed graph is said to be strongly connected only if every pair of distinct
vertices are connected.
In a weakly connected graph the nodes cannot be visited by a single path.
Strongly / Weakly Connected Directed Graphs
Fig: 08 strong and weakly connected graph

11. 11
Two graphs are isomorphic if and only if after recording the vertices their adjacency
matrices are the same.
Isomorphism
Isomorphic Not Isomorphic
Fig: 09 Isomorphism

12. 12