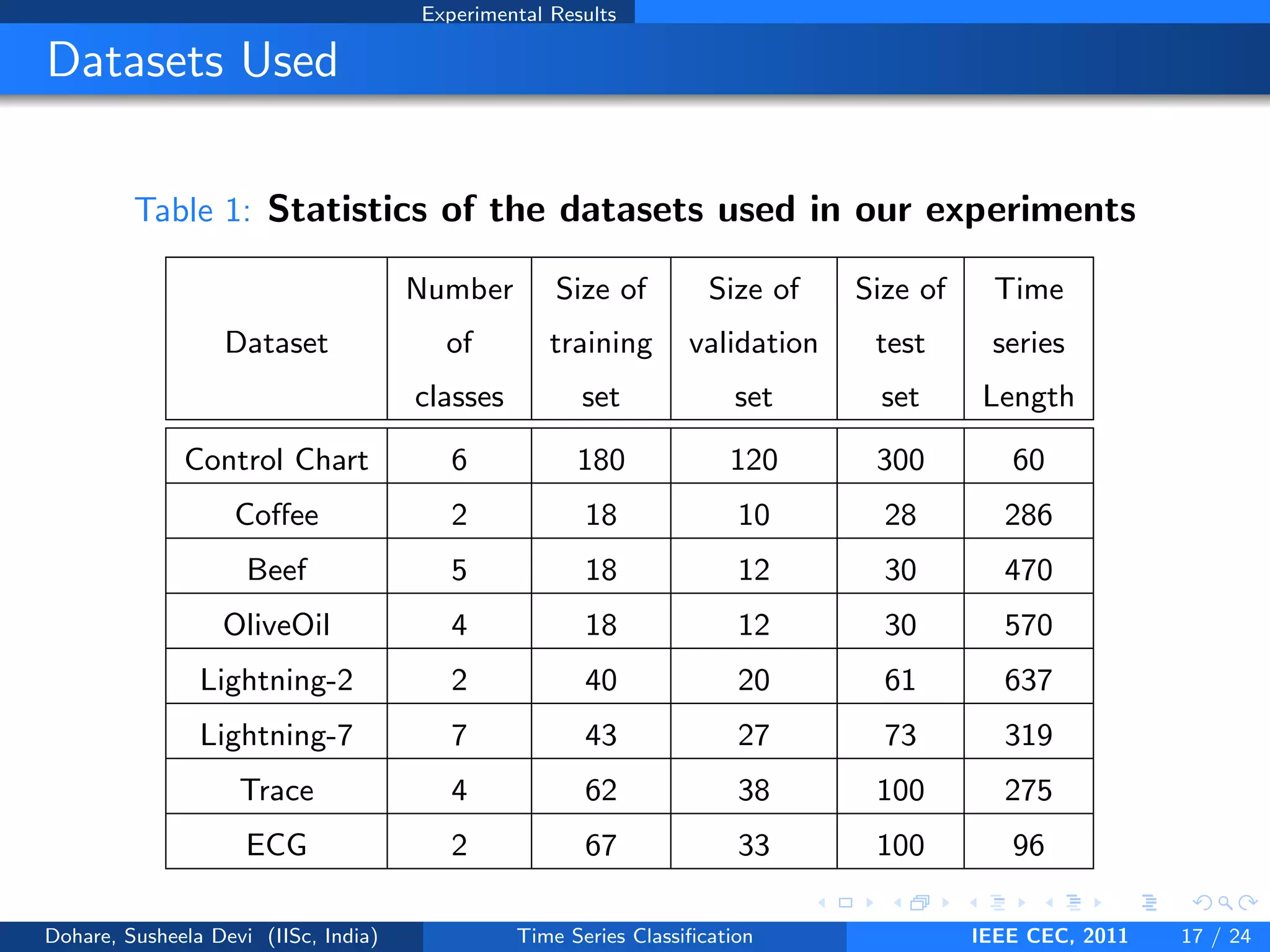
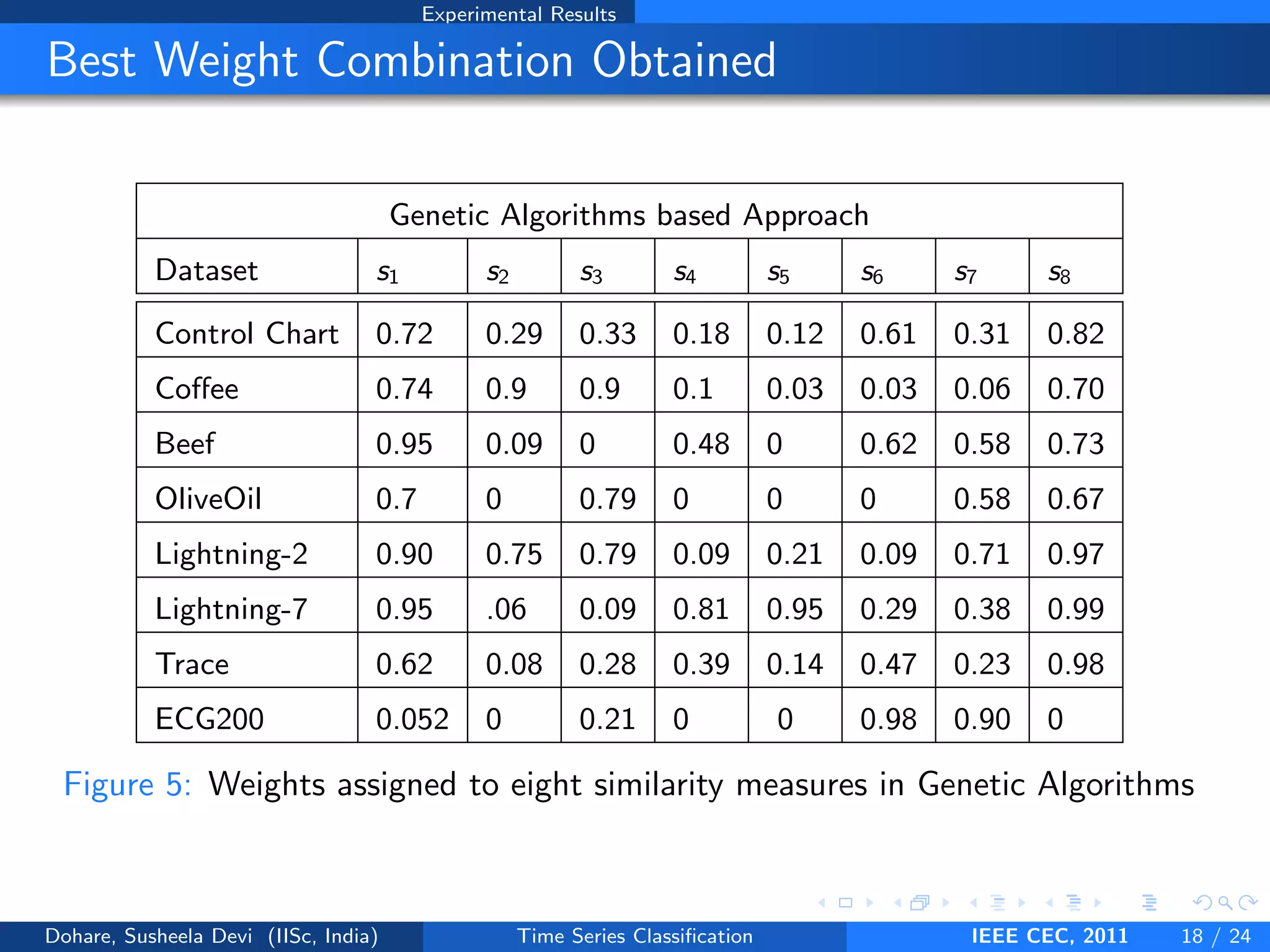
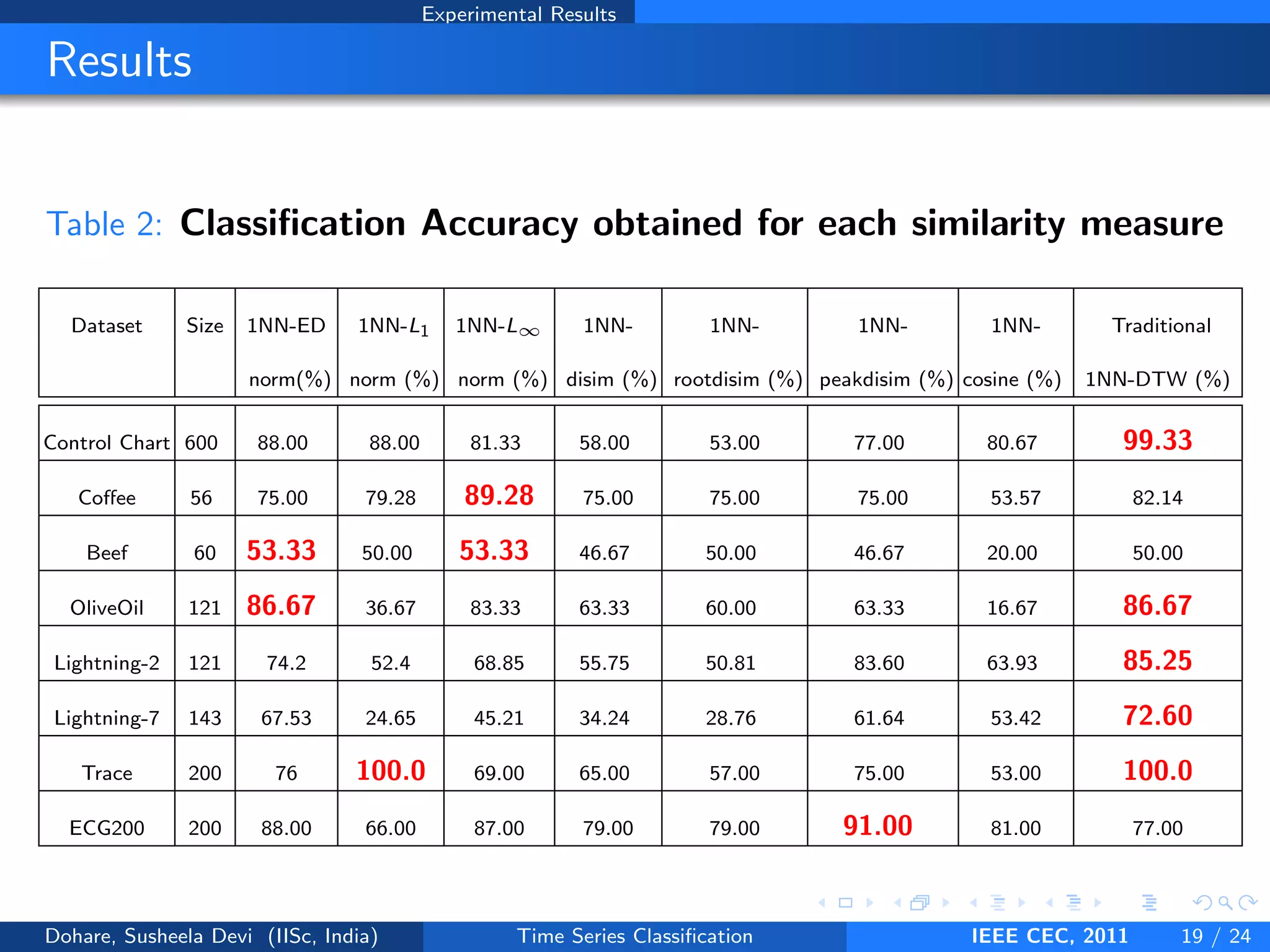
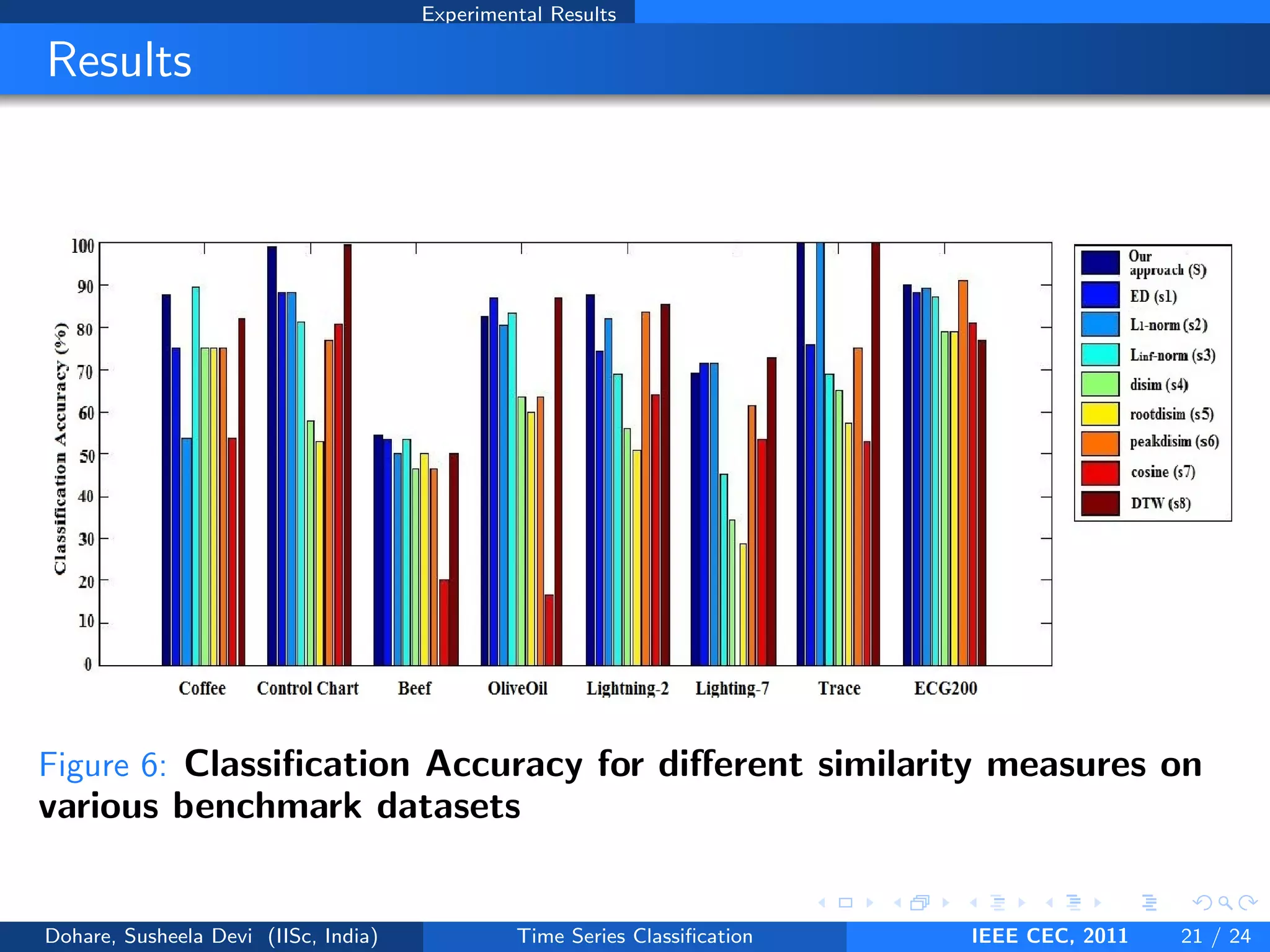
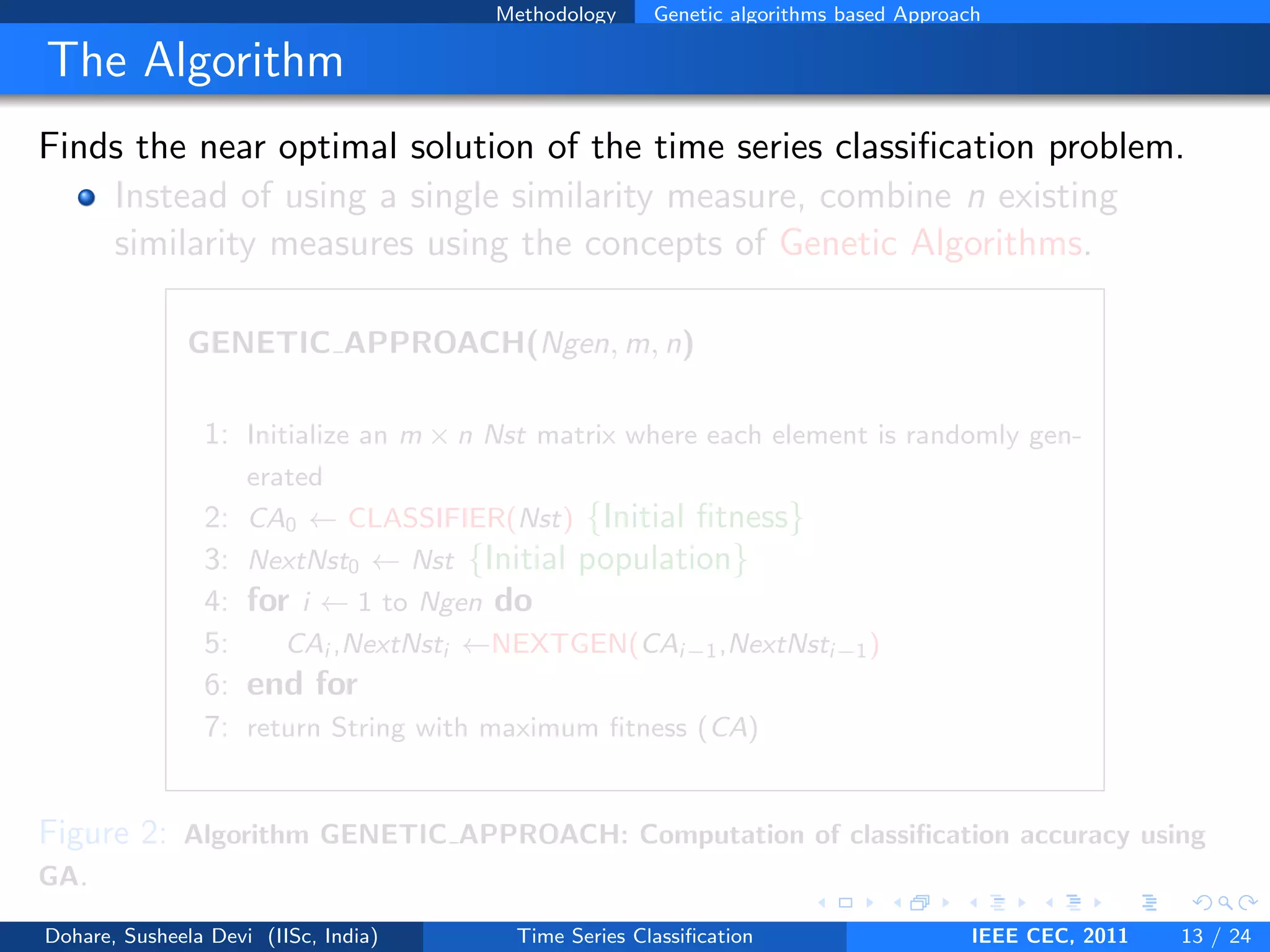
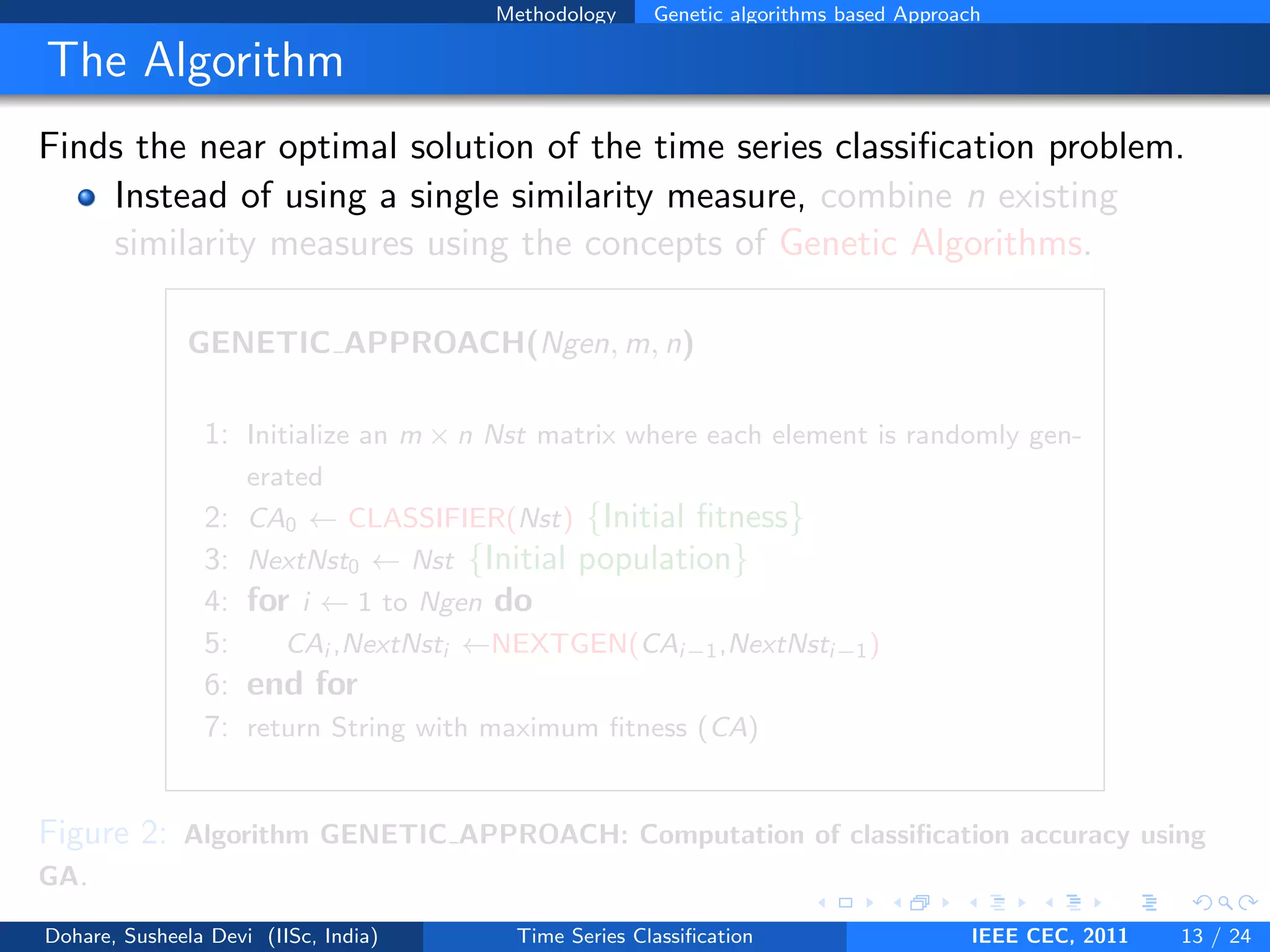
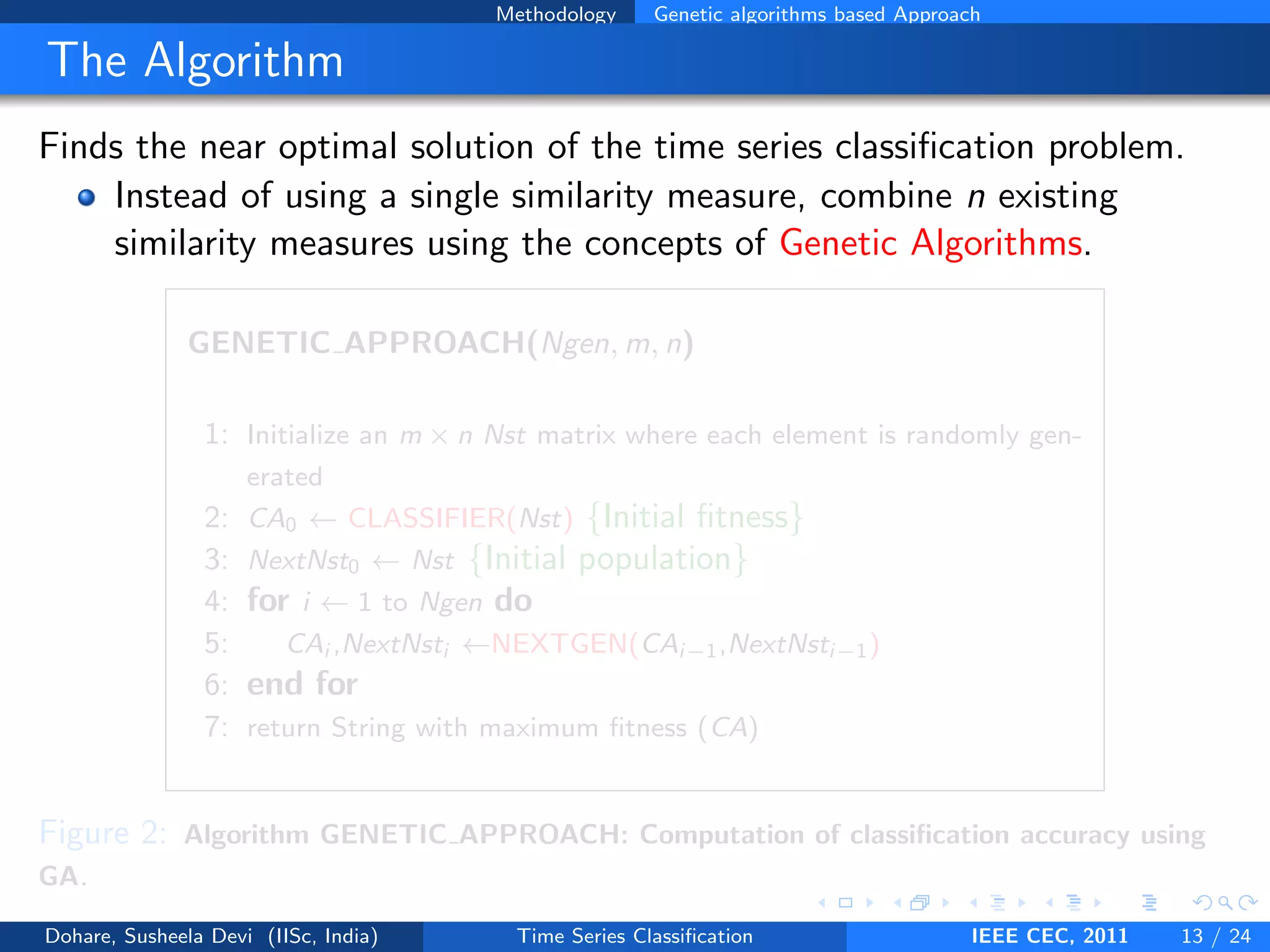
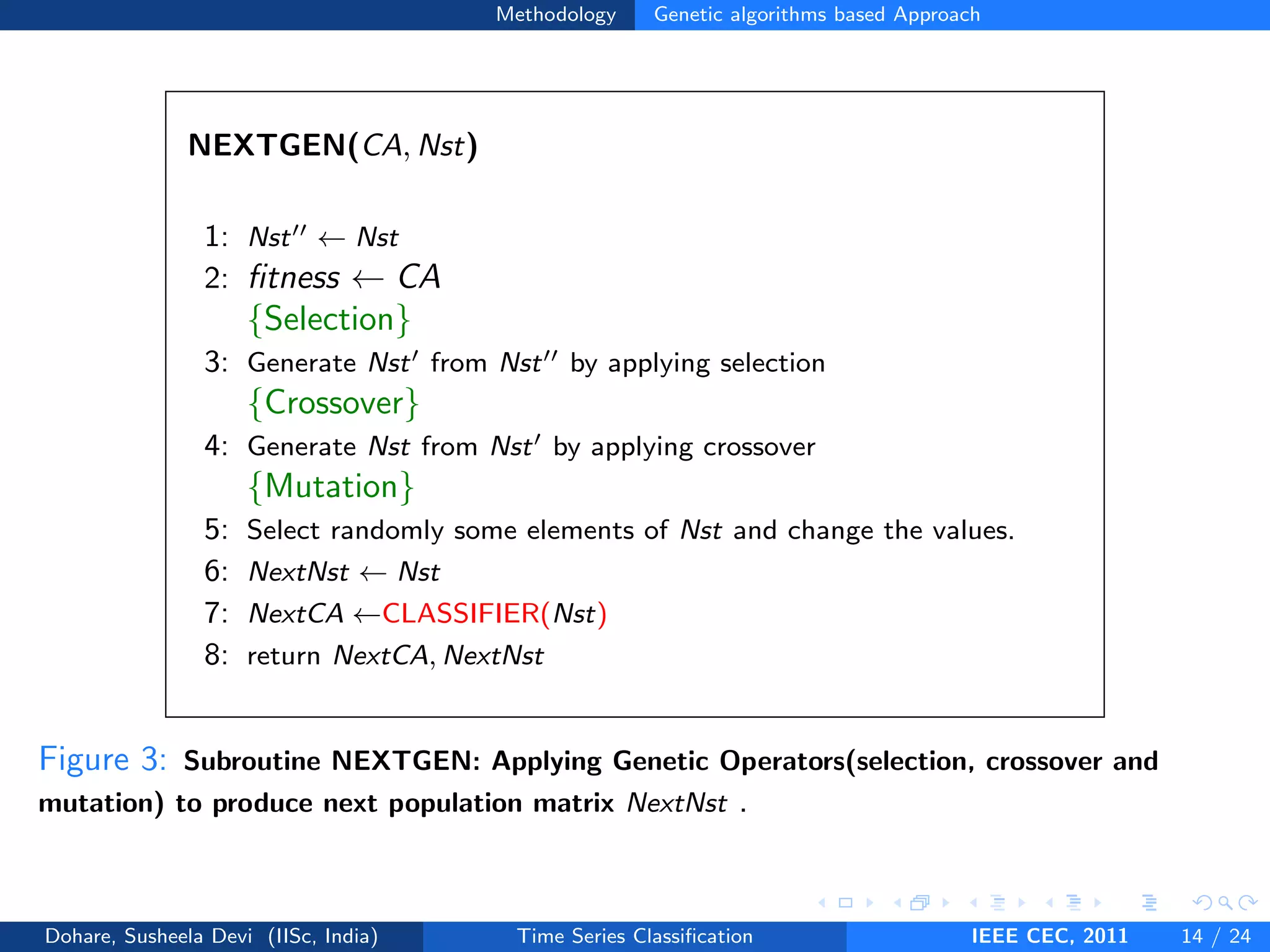
This document describes a genetic algorithm approach for time series classification that combines multiple similarity measures. The algorithm uses genetic operations like selection, crossover and mutation to evolve a population of weight combinations for different similarity measures over generations. The weight combinations represent candidate solutions, and classification accuracy on a validation set is used as the fitness function. The final solution returned is the weight combination that yields the highest classification accuracy.

1. Combination of Similarity Measures for Time
Series Classification using Genetic Algorithms
Deepti Dohare and V. Susheela Devi
Department of Computer Science and Automation
Indian Institute of Science, India
{deeptidohare, susheela}@csa.iisc.ernet.in
IEEE CEC, 2011
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 1 / 24

2. Outline
1 Introduction
2 Related Work
3 Motivation
4 Methodology
Genetic Algorithms
Genetic algorithms based Approach
5 Experimental Results
6 Conclusions and Future Work
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 2 / 24

3. Introduction
Introduction: Time Series Data
Definition
A time series t = {t1, ..., tr }, is an ordered set of r data points. Here the
data points, {t1, ..., tr }, are typically measured at successive point of time
spaced at uniform time intervals.
Figure 1: US population: An example of a time series
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 3 / 24

4. Introduction
Introduction: Time Series Classification
Definition
Given a set of class labels L, the task of time series classification is to learn
a classifier C, which is a function that maps a time series t to a class label
l ∈ L, written as C : t → l.
Applications
Cardiology
Intrusion Detection
Information Retrieval
Genomic Research
Signal Classification
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 4 / 24

5. Introduction
Time Series Classification Methods
Methods
Distance based classification methods
Require a measure to compute the distance or similarity between pair
of time series
Feature based classification methods
Transform a time series data into a feature vector and then apply
conventional classification methods
Model based classification methods
Use a model such as Hidden Markov Model (HMM) or other
statistical models to classify time series data
In this work, we have explored Distance Based Classification Methods
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 5 / 24

6. Related Work
Distance Based Classification Methods
Ding et al. [VLDB] (2008)1
For large datasets, the accuracy of elastic measures (DTW, LCSS,
EDR, ERP, etc.) converges with Euclidean distance (ED)
For small datasets, elastic measures can be significantly more accurate
than ED and other lock step measures
The efficiency of a similarity measure depends critically on the size of
the dataset
Keogh and Kassetty [SIGKDD] (2002)2
One nearest neighbour with Euclidean distance (1NN-ED) is very
difficult to beat
Novel similarity measures should be compared to simple strawmen,
such as Euclidian distance or Dynamic Time Warping.
1
H. Ding, G. Trajcevski, P. Scheuermann, X. Wang, and E. Keogh, Querying and mining of time series data: experimental
comparison of representations and distance measure, VLDB, 2008
2
E. Keogh and S. Kasetty, On the need for time series data mining benchmarks: A survey and empirical demonstration.
8th ACM SIGKDD, 2002
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 6 / 24

7. Related Work
Xi et al. [ICML] (2006)3
DTW is more accurate than ED for small datasets
Use numerical reduction to speed up DTW computation
Lee et al. [SIGMOD] (2007)4
The edit distance based similarity measures (LCSS, EDR, ERP) capture
the global similarity between two sequences, but not there local
similarity during a short time interval
3
Xiaopeng Xi, Eamonn Keogh, Christian Shelton, Li Wei and Chotirat Ann Ratanamahatana. Fast time series classification
using numerosity reduction. In ICML06, pages 1033-1040, 2006.
4
Jae-Gil Lee, Jiawei Han, and Kyu-Young Whang. Trajectory clustering: a partition-and-group framework. In Proceedings
of the 2007 ACM SIGMOD international conference on Management of data, SIGMOD 07, pages 593-604, New York, USA,
2007. ACM.
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 7 / 24

8. Motivation
Motivation
Different Similarity Measures
Performance may depend on datasets
How to find the best similarity measure
Why to depend only on one similarity measure
Intuition
Can we automatically identify the best similarity measure with respect
to the dataset?
Can we combine different similarity measures into one and use the
resultant similarity measures such that an inefficient similarity
measure will not affect the combination?
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 8 / 24

9. Motivation
Motivation
Different Similarity Measures
Performance may depend on datasets
How to find the best similarity measure
Why to depend only on one similarity measure
Intuition
Can we automatically identify the best similarity measure with respect
to the dataset?
Can we combine different similarity measures into one and use the
resultant similarity measures such that an inefficient similarity
measure will not affect the combination?
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 8 / 24

10. Motivation
Motivation
Different Similarity Measures
Performance may depend on datasets
How to find the best similarity measure
Why to depend only on one similarity measure
Intuition
Can we automatically identify the best similarity measure with respect
to the dataset?
Can we combine different similarity measures into one and use the
resultant similarity measures such that an inefficient similarity
measure will not affect the combination?
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 8 / 24

11. Motivation
Proposal
Design an algorithm that assign weights to similarity measures based
on their performance
Genetic Algorithms can be used to combine different similarity
measures
Our Aim
To combine different similarity measures (s1, s2, . . . , sn) by assigning them
some weights (w1, w2, . . . , wn) based on their performance. A new
similarity measure (Snew ) is obtained such that
Snew =
n
X
i=1
wi · si
where n is the number of similarity measures.
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 9 / 24

12. Methodology Genetic Algorithms
Genetic Algorithms (GA)
Finds an almost optimal solution to the problem
Operates on population of many solutions from the search space
Evolutionary Process: The population of solutions is evolved to
produce new generations of solutions by using genetic operators:
Selection
Crossover
Mutation
Fitness function: A function which estimates how capable the
candidate solution is of solving the problem
Average fitness of the candidate solution is improved at each step of
the evolutionary process
Search stops when the evolutionary process has reached the maximum
number of generations
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 10 / 24

13. Methodology Genetic Algorithms
In Our Context
Given n similarity measures
s1 s2 s3 . . . sn
↑ ↑ ↑ . . . ↑
w1 w2 w3 . . . wn
The weight combination (w1, w2, . . . , wn) is considered as a candidate
solution in the GA.
Using the above weight combination, new similarity measure is
obtained: Snew = Σ(si × wi )
Snew is then used to get the Classification Accuracy (CA)
Thus, the measure of CA is the fitness function in our case
Fitness Function −
−
−
→ Classification Accuracy
Candidate Solution −
−
−
→ Weight Combination
Final Solution −
−
−
→ best Weight Combination
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 11 / 24

14. Methodology Genetic Algorithms
Our Approach
Divide the original training set into two sets: the training set and the
validation set
The proposed GENETIC APPROACH gives the best combination of
weights W :
W = [w1, w2, . . . , wn]
for n similarity measures using the training set and the validation set
Resultant weights are assigned to the different similarity measures
which are combined to yield the new similarity measure Snew :
Snew = s1.w1 + s2.w2 + · · · + sn.wn
Snew is then used to classify the test data using 1NN
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 12 / 24

15. Methodology Genetic algorithms based Approach
The Algorithm
Finds the near optimal solution of the time series classification problem.
Instead of using a single similarity measure, combine n existing
similarity measures using the concepts of Genetic Algorithms.
GENETIC APPROACH(Ngen, m, n)
1: Initialize an m × n Nst matrix where each element is randomly gen-
erated
2: CA0 ← CLASSIFIER(Nst) {Initial fitness}
3: NextNst0 ← Nst {Initial population}
4: for i ← 1 to Ngen do
5: CAi ,NextNsti ←NEXTGEN(CAi−1,NextNsti−1)
6: end for
7: return String with maximum fitness (CA)
Figure 2: Algorithm GENETIC APPROACH: Computation of classification accuracy using
GA.
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 13 / 24

16. Methodology Genetic algorithms based Approach
The Algorithm
Finds the near optimal solution of the time series classification problem.
Instead of using a single similarity measure, combine n existing
similarity measures using the concepts of Genetic Algorithms.
GENETIC APPROACH(Ngen, m, n)
1: Initialize an m × n Nst matrix where each element is randomly gen-
erated
2: CA0 ← CLASSIFIER(Nst) {Initial fitness}
3: NextNst0 ← Nst {Initial population}
4: for i ← 1 to Ngen do
5: CAi ,NextNsti ←NEXTGEN(CAi−1,NextNsti−1)
6: end for
7: return String with maximum fitness (CA)
Figure 2: Algorithm GENETIC APPROACH: Computation of classification accuracy using
GA.
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 13 / 24

17. Methodology Genetic algorithms based Approach
The Algorithm
Finds the near optimal solution of the time series classification problem.
Instead of using a single similarity measure, combine n existing
similarity measures using the concepts of Genetic Algorithms.
GENETIC APPROACH(Ngen, m, n)
1: Initialize an m × n Nst matrix where each element is randomly gen-
erated
2: CA0 ← CLASSIFIER(Nst) {Initial fitness}
3: NextNst0 ← Nst {Initial population}
4: for i ← 1 to Ngen do
5: CAi ,NextNsti ←NEXTGEN(CAi−1,NextNsti−1)
6: end for
7: return String with maximum fitness (CA)
Figure 2: Algorithm GENETIC APPROACH: Computation of classification accuracy using
GA.
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 13 / 24

18. Methodology Genetic algorithms based Approach
The Algorithm
Finds the near optimal solution of the time series classification problem.
Instead of using a single similarity measure, combine n existing
similarity measures using the concepts of Genetic Algorithms.
GENETIC APPROACH(Ngen, m, n)
1: Initialize an m × n Nst matrix where each element is randomly gen-
erated
2: CA0 ← CLASSIFIER(Nst) {Initial fitness}
3: NextNst0 ← Nst {Initial population}
4: for i ← 1 to Ngen do
5: CAi ,NextNsti ←NEXTGEN(CAi−1,NextNsti−1)
6: end for
7: return String with maximum fitness (CA)
Figure 2: Algorithm GENETIC APPROACH: Computation of classification accuracy using
GA.
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 13 / 24

19. Methodology Genetic algorithms based Approach
NEXTGEN(CA, Nst)
1: Nst00 ← Nst
2: fitness ← CA
{Selection}
3: Generate Nst0 from Nst00 by applying selection
{Crossover}
4: Generate Nst from Nst0 by applying crossover
{Mutation}
5: Select randomly some elements of Nst and change the values.
6: NextNst ← Nst
7: NextCA ←CLASSIFIER(Nst)
8: return NextCA, NextNst
Figure 3: Subroutine NEXTGEN: Applying Genetic Operators(selection, crossover and
mutation) to produce next population matrix NextNst .
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 14 / 24

20. Methodology Genetic algorithms based Approach
CLASSIFIER(Nst)
1: for i ← 1 to m do
2: for j ← 1 to length(Test Class labels) do
3: best so far ← inf
4: for k ← 1 to length(Train Class labels) do
5: x←training pattern
6: y←test pattern
7: Compute s1, s2, ..., sn distance function for x and y
8: S[i] ← s1 ∗ Nst[i][1] + s2 ∗ Nst[i][2] + .... + sn ∗ Nst[i][n]
9: if S[i] < best so far then
10: Predicted class ← Train Class labels[k]
11: end if
12: end for
13: if predicted class is same as the actual class then
14: correct ← correct + 1
15: end if
16: end for
17: CA[i] ← (correct/length(Test Class labels)) ∗ 100
18: end for
19: return CA
Figure 4: Subroutine CLASSIFIER: Computation of CA for one population matrix Nst of
size m × n .
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 15 / 24

21. Experimental Results
The Algorithm in Action
Similarity Measures
1 Euclidean Distance (L2 norm) s1(p, q) =
qPn
i=1
(pi − qi )2
2 Manhattan Distance (L1 norm) s2(p, q) =
Pn
i=1 |(pi − qi )|
3 Maximum Norm (L∞ norm) s3(p, q) = max(|(p1 − q1)|, . . . , |(pn − qn)|)
4 Mean dissimilarity s4(p, q) = 1
n
.
Pn
i=1
|pi −qi |
|pi |+|qi |
5 Root Mean Square Dissimilarity s5(p, q) =
q
1
n
.
Pn
i=1
dissim(pi , qi )2
6 Peak Dissimilarity s6(p, q) = 1
n
.
Pn
i=1
|pi −qi |
2.max(|pi |,|qi |)
7 Cosine Distance s7(p, q) = cos(θ) = p.q
kpkkqk
8 DTW Distance s8(p, q) = min
(
qPK
k=1
wk /K
)
where max(|p|, |q|)≤ K < |p| + |q| − 1
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 16 / 24

22. Experimental Results
Datasets Used
Table 1: Statistics of the datasets used in our experiments
Number Size of Size of Size of Time
Dataset of training validation test series
classes set set set Length
Control Chart 6 180 120 300 60
Coffee 2 18 10 28 286
Beef 5 18 12 30 470
OliveOil 4 18 12 30 570
Lightning-2 2 40 20 61 637
Lightning-7 7 43 27 73 319
Trace 4 62 38 100 275
ECG 2 67 33 100 96
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 17 / 24

23. Experimental Results
Best Weight Combination Obtained
Genetic Algorithms based Approach
Dataset s1 s2 s3 s4 s5 s6 s7 s8
Control Chart 0.72 0.29 0.33 0.18 0.12 0.61 0.31 0.82
Coffee 0.74 0.9 0.9 0.1 0.03 0.03 0.06 0.70
Beef 0.95 0.09 0 0.48 0 0.62 0.58 0.73
OliveOil 0.7 0 0.79 0 0 0 0.58 0.67
Lightning-2 0.90 0.75 0.79 0.09 0.21 0.09 0.71 0.97
Lightning-7 0.95 .06 0.09 0.81 0.95 0.29 0.38 0.99
Trace 0.62 0.08 0.28 0.39 0.14 0.47 0.23 0.98
ECG200 0.052 0 0.21 0 0 0.98 0.90 0
Figure 5: Weights assigned to eight similarity measures in Genetic Algorithms
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 18 / 24

24. Experimental Results
Results
Table 2: Classification Accuracy obtained for each similarity measure
Dataset Size 1NN-ED 1NN-L1 1NN-L∞ 1NN- 1NN- 1NN- 1NN- Traditional
norm(%) norm (%) norm (%) disim (%) rootdisim (%) peakdisim (%) cosine (%) 1NN-DTW (%)
Control Chart 600 88.00 88.00 81.33 58.00 53.00 77.00 80.67 99.33
Coffee 56 75.00 79.28 89.28 75.00 75.00 75.00 53.57 82.14
Beef 60 53.33 50.00 53.33 46.67 50.00 46.67 20.00 50.00
OliveOil 121 86.67 36.67 83.33 63.33 60.00 63.33 16.67 86.67
Lightning-2 121 74.2 52.4 68.85 55.75 50.81 83.60 63.93 85.25
Lightning-7 143 67.53 24.65 45.21 34.24 28.76 61.64 53.42 72.60
Trace 200 76 100.0 69.00 65.00 57.00 75.00 53.00 100.0
ECG200 200 88.00 66.00 87.00 79.00 79.00 91.00 81.00 77.00
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 19 / 24

25. Experimental Results
Results
Table 3: Comparison of our approaches and best similarity measures
(from Table 2)
Dataset Size 1NN-GA (%) Best Similarity Measure
(mean ± st.dev.) (From Table 2) (%)
Control Chart 600 99.07 ± 0.37 DTW (99.33)
Coffee 56 87.50 ± 2.06 L∞ norm (89.28)
Beef 60 54.45 ± 1.92 ED, L∞ norm (53.33)
OliveOil 121 82.67 ± 4.37 ED, DTW (86.67)
Lightning-2 121 87.54 ± 1.47 DTW (85.25)
Lightning-7 143 69.28 ± 2.97 DTW (72.6)
Trace 200 100.0 ± 0.00 L1 norm, DTW (100)
ECG200 200 90.00 ± 1.15 peakdisim (91)
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 20 / 24

26. Experimental Results
Results
Figure 6: Classification Accuracy for different similarity measures on
various benchmark datasets
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 21 / 24

27. Conclusions and Future Work
Conclusions
We have presented a novel approach for time series classification
based on Genetic Algorithms.
Inefficient similarity measure does not affect the proposed algorithm
as it will be simply discarded.
The implementation of the proposed algorithm has shown that the
results obtained using our approach are considerably better.
At the end of the algorithm, the weights obtained are optimal in the
sense that they are biased towards the most appropriate optimal
measure.
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 22 / 24

28. Conclusions and Future Work
Future Work
It would be interesting to see whether genetic algorithms based
approaches can be applied to various other kinds of datasets with
little or no modification, for example, streaming datasets
Numerical representation methods for dimensionality reduction could
be used to improve the proposed approach
The algorithm can be used with any distance based classifier
Other similarity measures can also be used in the proposed approach
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 23 / 24

29. THANK YOU
Dohare, Susheela Devi (IISc, India) Time Series Classification IEEE CEC, 2011 24 / 24