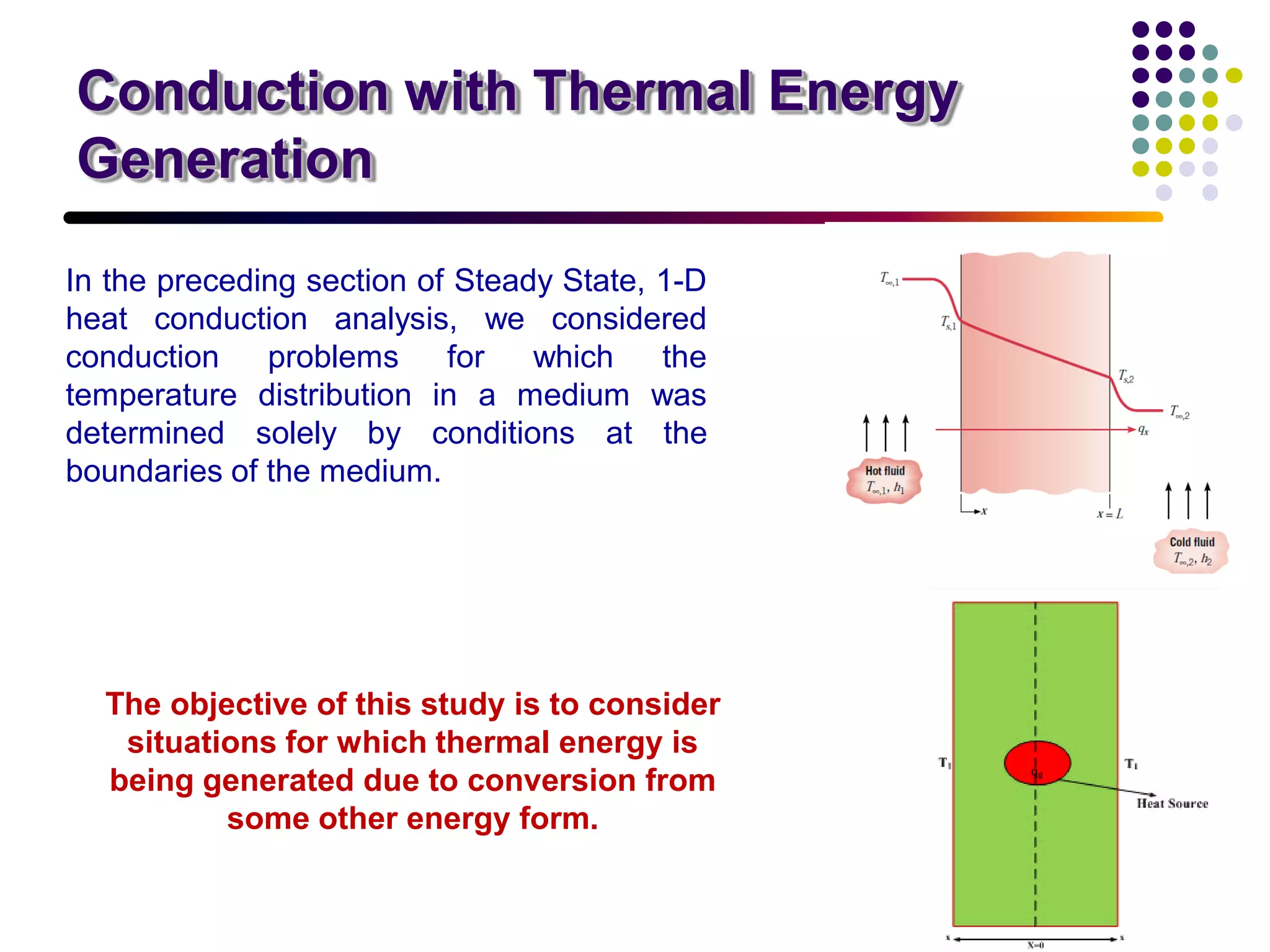
The document discusses heat transfer with a focus on conduction involving thermal energy generation due to processes like chemical reactions and electrical resistance. It provides detailed analysis on temperature distribution in plane walls and cylindrical components under steady-state conditions, highlighting the influence of boundary conditions on the heat transfer process. Various equations and methodologies for estimating surface temperatures and temperature gradients are presented, emphasizing their applicability to isotropic materials.

1. 20ME301T – Heat Transfer
Dr. Rajesh Patel
Mechanical Engineering Department
School of Technology
Pandit Deendayal Petroleum University
Conduction with Thermal Energy
Generation

2. Conduction with Thermal Energy
Generation
In the preceding section of Steady State, 1-D
heat conduction analysis, we considered
conduction problems for which the
temperature distribution in a medium was
determined solely by conditions at the
boundaries of the medium.
The objective of this study is to consider
situations for which thermal energy is
being generated due to conversion from
some other energy form.

3. Conduction with Thermal Energy
Generation
A common thermal energy generation process involves:
 Exothermic Chemical Reaction
 Conversion from electrical to thermal energy in a
current-carrying medium (Ohmic, or resistance, or
Joule heating).
The rate at which energy is generated by
passing a current I through a medium of
electrical resistance Re is

4. Conduction with Thermal Energy
Generation
If this power generation (W) occurs uniformly
throughout the medium of volume V, the
volumetric generation rate (W/m3) is then

5. Heat Conduction with Thermal Energy
Generation in a Plane Wall
Consider the plane wall with uniform energy generation per unit volume
( is constant) and the surfaces are maintained at Ts,1 and Ts,2.

6. Heat Conduction with Thermal Energy
Generation in a Plane Wall
For steady state, 1-D heat conduction with heat
generation in a isotropic material (constant thermal
conductivity k), above equation will be reduced to
(1)
The general solution of Eqn. (1) is given by
(2)

7. Heat Conduction with Thermal Energy
Generation in a Plane Wall
(2)
Boundary Conditions:
B.C - I At x = -L T(-L) = Ts,1 (3)
B. C –II At x = L T(L) = Ts,2 (4)
Substituting B.C’s in Eqn. (2) , The constants may be evaluated as
(5)
Substituting constants
C1 and C2 in Eqn. (2)

8. Heat Conduction with Thermal Energy
Generation in a Plane Wall
Eqn. (6) represents the temperature distribution
(6)

9. Heat Conduction with Thermal Energy
Generation in a Plane Wall
(6)
Case-I: Symmetric boundary conditions
The temperature distribution is then symmetrical about
the mid-plane as shown in Figure. Ts,1 = Ts,2 = Ts
For the symmetric boundary conditions, Eqn. (6)
will be reduced to;
(7)

10. Heat Conduction with Thermal Energy
Generation in a Plane Wall
Case-I: Symmetric boundary conditions
(7)
The maximum temperature exists at the mid-
plane (x=0)
(8)
Combining Eqn. (7) and (8), temperature distribution can be written as;
(9)

11. Heat Conduction with Thermal Energy
Generation in a Plane Wall
Case-I: Symmetric boundary conditions
 Note that at the plane of symmetry in Figure, the
temperature gradient is zero, (dT/dx)x=0 = 0.
 Accordingly, there is no heat transfer across this
plane, and it may be represented by the
adiabatic surface
(9)

12. Heat Conduction with Thermal Energy
Generation in a Plane Wall
Case-I: Symmetric boundary conditions
(9)
Above results (equations) can be applied to
plane walls that are perfectly insulated on one
side (x=0) and maintained at a fixed temperature
Ts on the other side (x = L).

13. Heat Conduction with Thermal Energy
Generation in a Plane Wall
Case-I: Symmetric boundary conditions
Estimation of surface temperature Ts
Applying the energy balance at the surface at x = L
(Heat Conduction at surface at x = L) = (Heat
convection from surface x = L)
(1)
(2)

14. Heat Conduction with Thermal Energy
Generation in a Plane Wall
Case-I: Symmetric boundary conditions
(1)
(2)
Getting value of (dT/dx)x=L from Eqn. (1)
and substituting in Eqn. (2)
(3)

15. Radial Heat Conduction with Thermal
Energy Generation in a Cylinder
For steady-state conditions the rate at which heat
is generated within the cylinder must equal the
rate at which heat is convected from the surface
of the cylinder to a moving fluid.
For steady state,radial heat conduction with heat generation in a isotropic
material (constant thermal conductivity k), above equation will be reduced to
(1)
(2)

16. Radial Heat Conduction with Thermal
Energy Generation in a Cylinder
(2)
Integrating above equation twice, the general
solution for the temperature distribution can be
written as;
(3)
Boundary Conditions:
B.C - I At r = 0 (dT/dr) r=0) = 0 (4)
B. C –II At r = r T = Ts (5)
Substituting B.C’s into Eqn. (3), C1 and C2 can be estimated as;

17. Radial Heat Conduction with Thermal
Energy Generation in a Cylinder
(2)
(3)
Substituting C1 and
C2 into Eqn. (3)
(4)
Represents temperature distribution
For steady state radial heat
conduction with heat generation on
cylindrical component

18. Radial Heat Conduction with Thermal
Energy Generation in a Cylinder
Centerline temperature can be evaluated as
(4)
(5)
From Eqn (4) and (5), the temperature distribution in non-dimensional form
can be written as

19. Radial Heat Conduction with Thermal
Energy Generation in a Cylinder
(4)
Estimation of surface temperature Ts
From Overall Energy balance
(Heat Generation rate in system) = (Heat Convection from Surface)