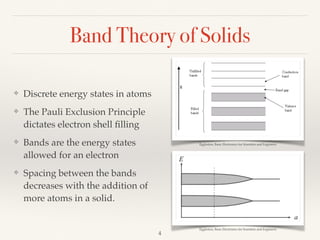
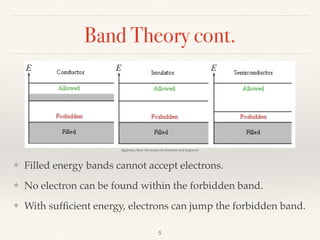
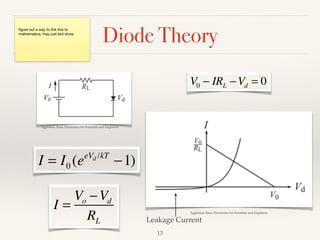
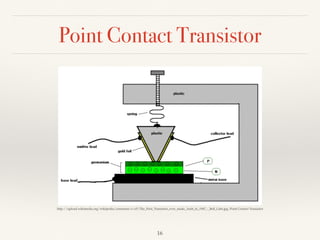
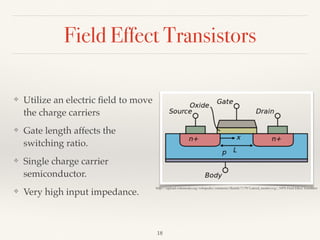
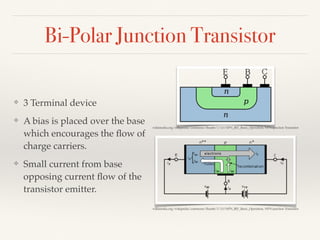
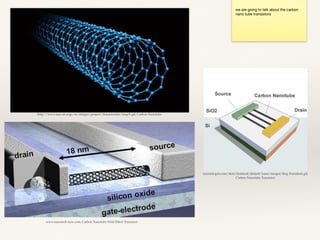
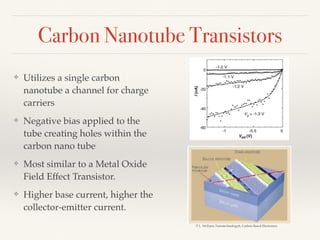
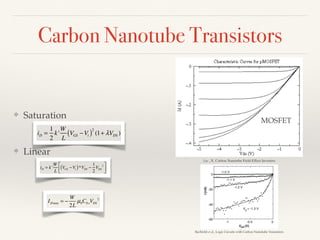
The document summarizes the transition from glass tube transistors to carbon nanotube transistors. It begins by discussing band theory and how doping semiconductors creates an excess or deficiency of charge carriers. Early transistors were based on germanium and the discovery that current could flow between gold and tungsten contacts on a germanium sample with a bias. The document then covers point contact transistors, field effect transistors, bipolar junction transistors and their operating characteristics. Finally, it discusses how carbon nanotube transistors can be used to build logic gates and their advantages over traditional transistors, including flexibility, heat dissipation and ability to be scaled down further.

1. From Glass Tubes to
Carbon Nanotubes
Kevin Kuwata
Monday, March 30, 2015
Department of Physics,
Occidental College
The Transition of the Transistor
1
http://thumbs.dreamstime.com/
Bachtold et al., Science, Logic Circuits with Carbon Nanotube Transistors

2. Overview
❖ What is a Transistor?
❖ Band Theory
❖ History
❖ Breakthrough Applications
2

3. What is a Transistor?
❖ Electrical Switch
❖ Signal Amplifier
❖ Voltage Rectifier
❖ Temperature Sensor
3
tandyonline.co.uk, 2n2222

4. Band Theory of Solids
❖ Discrete energy states in atoms
❖ The Pauli Exclusion Principle
dictates electron shell filling
❖ Bands are the energy states
allowed for an electron
❖ Spacing between the bands
decreases with the addition of
more atoms in a solid.
4
Eggleston, Basic Electronics for Scientists and Engineers
Eggleston, Basic Electronics for Scientists and Engineers

5. Band Theory cont.
5
❖ Filled energy bands cannot accept electrons.
❖ No electron can be found within the forbidden band.
❖ With sufficient energy, electrons can jump the forbidden band.
Eggleston, Basic Electronics for Scientists and Engineers

6. Jumping Bands
6
Eggleston, Basic Electronics for Scientists and Engineers

7. Doping Semiconductors
❖ The process of including impurities in a pure
semiconducting material in hopes to engineer specific
electrical characteristics for a semiconducting material
❖ Increases number of charge carriers present in a
material
❖ P-Type
❖ N-Type
7

8. N-Type Semiconductors
❖ Majority charge carriers are
negative (electrons)
❖ The dopant introduces
localized energy bands
8
Eggleston, Basic Electronics for Scientists and Engineers
http://hyperphysics.phy-astr.gsu.edu/, Antimony Valence Electrons

9. P-Type Semiconductors
❖ Majority charge carriers are
holes
❖ Introduce an intermediate
energy level within the
forbidden band, which the
electrons can jump.
http://hyperphysics.phy-astr.gsu.edu/, Boron Valence Electrons
Eggleston, Basic Electronics for Scientists and Engineers
9

10. now we are transitioning to the theory of
a transistor. we will talk about each
image and say hey were gonna just
start simple with the diode but this is
where we are headed.
sdigital-components.com, Transistors
wikimedia.org/wikipedia/commons/e/e5/The_First_Transisto, Bell Labs
http://d1gsvnjtkwr6dd.cloudfront.net/large/SC-DI-1N5391_LRG.jpg
http://hyperphysics.phy-astr.gsu.edu/hbase/solids/imgsol/tran1.gif
10

11. Diode Theory
❖ Fermi-Dirac Distribution
f (E) =
1
e(E−EF )/kT
+1
N = e−E/kT
Eo+∆ E
∞
∫ dE = −kt e−∞
− e−(E0 +∆ E)/kT
⎡⎣ ⎤⎦
f1 = Ce−∆ E/kT
f2 = Ce−∆ E/kT
fnet = Ce−´∆ E/kT
eeV0 /kT
−1( )
I0 ≡ Ce−´∆ E/kT
I0
graph so as temperature rises the
energy will too and it will be easier to go
from n to p
(also think about mentioning Fermi
level, simply just the location within
energy band closer or farther from
conduction band
Eggleston, Basic Electronics for Scientists and Engineers
11

12. V0 − IRL −Vd = 0
Diode Theory
❖ Model the voltage drop over a
diode as 0.6 volts under
forward bias operation.
❖ Kirchhoff Voltage Loop:
I = I0 (eeVd /kT
−1)
Eggleston, Basic Electronics for Scientists and Engineers
Eggleston, Basic Electronics for Scientists and Engineers
http://d1gsvnjtkwr6dd.cloudfront.net/large/SC-DI-1N5391_LRG.jpg
12

13. V0 − IRL −Vd = 0
Diode Theory
I = I0 (eeVd /kT
−1)
I =
Vo −Vd
RL Leakage Current
Eggleston, Basic Electronics for Scientists and Engineers
Eggleston, Basic Electronics for Scientists and Engineers
figure out a way to link this to
mathematica. may just exit show.
13

14. NOW we are talking about the top right
picture going to discuss the transistor
inplimentation of third lead, called the
base
sdigital-components.com, Transistors
wikimedia.org/wikipedia/commons/e/e5/The_First_Transisto, Bell Labs
http://d1gsvnjtkwr6dd.cloudfront.net/large/SC-DI-1N5391_LRG.jpg
http://hyperphysics.phy-astr.gsu.edu/hbase/solids/imgsol/tran1.gif
14

15. Transistors Basics
❖ A transistor is basically a
switch or valve.
❖ Characterized by an IV curve
similar to the diode, but a
family of curves.
❖ Beta
❖ Follow’s Moore’s Law.
wikimedia.org/wikipedia/commons/e/e5/The_First_Transisto, Bell Labs
15

16. Point Contact Transistor
http://upload.wikimedia.org/wikipedia/commons/e/e5/The_First_Transistor_ever_made,_built_in_1947_-_Bell_Labs.jpg, Point Contact Transistor
16

17. Point Contact Transistor
❖ Bias applied to n type germanium, holes created in
Germanium and current found to flow between gold
contact and tungsten contact.
17
http://upload.wikimedia.org/wikipedia/commons/e/e5/The_First_Transistor_ever_made,_built_in_1947_-_Bell_Labs.jpg, Point Contact Transistor

18. Field Effect Transistors
❖ Utilize an electric field to move
the charge carriers
❖ Gate length affects the
switching ratio.
❖ Single charge carrier
semiconductor.
❖ Very high input impedance.
http://upload.wikimedia.org/wikipedia/commons/thumb/7/79/Lateral_mosfet.svg/, NPN Field Effect Transistor
18

19. Bi-Polar Junction Transistor
❖ 3 Terminal device
❖ A bias is placed over the base
which encourages the flow of
charge carriers.
❖ Small current from base
opposing current flow of the
transistor emitter.
wikimedia.org/wikipedia/commons/thumb/1/13/NPN_BJT_Basic_Operation, NPN junction Transistor
wikimedia.org/wikipedia/commons/thumb/1/13/NPN_BJT_Basic_Operation, NPN junction Transistor

20. Bi-Polar Junction Transistor
❖ Load line analysis is used to
determine the base current of
the transistor
❖ We have a family of curves
describing the transistor
operation
Eggleston, Basic Electronics for Scientists and Engineers

21. Bi-Polar Junction Transistor
IC =
Vcc −Vce
Rc
Vcc − IcRc −Vce = 0
Ib =
V1 −Vbe
Rb
V1 − IbRb −Vbe = 0
Eggleston, Basic Electronics for
Scientists and Engineers
Eggleston, Basic Electronics for Scientists and Engineers
Eggleston, Basic Electronics for Scientists and Engineers

22. www.nanotech-now.com, Carbon Nanotube Field Effect Transistor
we are going to talk about the carbon
nano tube transistors
nanointegris.com/skin/frontend/default/nano/images/Img-Transitors.gif,
Carbon Nanotube Transistor
http://www.tasc-nt.or.jp/en/images/project/characteristic/img01.gif, Carbon Nanotube

23. Carbon Nanotube Transistors
❖ Utilizes a single carbon
nanotube a channel for charge
carriers
❖ Negative bias applied to the
tube creating holes within the
carbon nano tube
❖ Most similar to a Metal Oxide
Field Effect Transistor.
❖ Higher base current, higher the
collector-emitter current.
P. L. McEuen, Nanotechnologyh, Carbon-Based Electronics

24. Carbon Nanotube Transistors
❖ Saturation
❖ Linear
iD =
1
2
k'
W
L
VGS −Vt( )2
(1+ λVDS )
iD = k'
W
L
VGS −Vt( )*VDS −
1
2
VDS
2⎡
⎣⎢
⎤
⎦⎥
IDmax = −
W
2L
µ0C0xVDS
2
MOSFET
Bachtold et al., Logic Circuits with Carbon Nanotube Transistors
Liu , X. Carbon Nanotube Field-Effect Inverters

25. Carbon Nanotube Transistors Applications
❖ Traditional transistor
applications: amplifier, switch
❖ Logic Gates
❖ And, Or, NOR, Inverter
Liu , X. Carbon Nanotube Field-Effect Inverters

26. Carbon Nanotube Transistors
❖ Hard to place single carbon
nanotubes
❖ Carbon Nanotubes degrade
quickly when exposed to
oxygen
❖ Better flexibility of actual
bonds (flexible electronics)
❖ Heat dissipation
❖ Small temperature
dependence on device
operation
❖ Smaller electronic devices,
easily scalable
❖ Some predict it will help re-
establish Moore’s Law.

27. Q & A