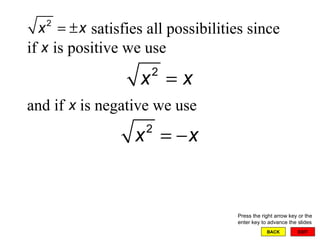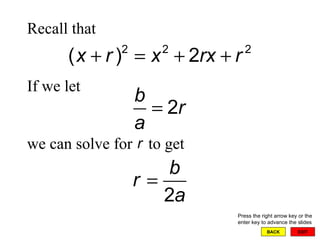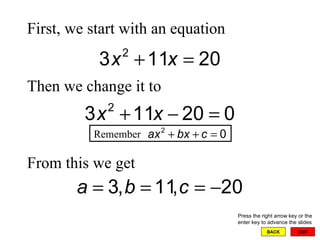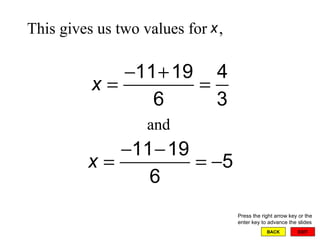The document discusses completing the square and solving quadratic equations. It explains that completing the square allows any quadratic equation to be written in the form (x - h)2 = k, which can then be solved using the square root property. The quadratic formula is derived from completing the square and provides a general method for solving any quadratic equation in one variable by setting it equal to 0 and substituting the coefficients into the formula. Examples are provided to demonstrate how to use completing the square and the quadratic formula to solve quadratic equations.

1. Completing the Square EXIT NEXT Click one of the buttons below or press the enter key

2. EXIT BACK The easiest quadratic equations to solve are of the type where r is any constant. Press the right arrow key or the enter key to advance the slides

3. EXIT BACK The solution to is Press the right arrow key or the enter key to advance the slides The answer comes from the fact that we solve the equation by taking the square root of both sides

4. EXIT BACK Since is a constant, we get where both sides are positive, but since is a variable it could be negative, yet is positive and is also positive. Press the right arrow key or the enter key to advance the slides

5. EXIT BACK If we write and is negative, we are saying that a positive number is negative, which it cannot be. To get around this contradiction we need to insist that Press the right arrow key or the enter key to advance the slides

6. EXIT BACK satisfies all possibilities since if is positive we use and if is negative we use Press the right arrow key or the enter key to advance the slides

7. EXIT BACK Thus, we get the solution for We generally change this equation by multiplying both sides by , then we simplify and get Press the right arrow key or the enter key to advance the slides

8. EXIT BACK We generally skip all the intermediate steps for an equation like and get Press the right arrow key or the enter key to advance the slides

9. EXIT BACK For quadratic equations such as we solve and get Press the right arrow key or the enter key to advance the slides

10. EXIT BACK For quadratic equations that are not expressed as an equation between two squares, we can always express them as If this equation can be factored, then it can generally be solved easily. Press the right arrow key or the enter key to advance the slides

11. EXIT BACK If the equation can be put in the form then we can use the square root method described previously to solve it. The solution for this equation is Press the right arrow key or the enter key to advance the slides The sign of m needs to be the opposite of the sign used in

12. EXIT BACK The question becomes: “Can we change the equation from the form to the form ?” Fortunately the answer is yes! Press the right arrow key or the enter key to advance the slides

13. EXIT BACK The procedure for changing is as follows. First, divide by , this gives Then subtract from both sides. This gives Press the right arrow key or the enter key to advance the slides

14. EXIT BACK We pause at this point to review the process of squaring a binomial. We will use this procedure to help us complete the square. Press the right arrow key or the enter key to advance the slides

15. EXIT BACK Recall that If we let we can solve for to get Press the right arrow key or the enter key to advance the slides

16. EXIT BACK Substituting in we get Using the symmetric property of equations to reverse this equation we get Press the right arrow key or the enter key to advance the slides

17. EXIT BACK Now we will return to where we left our original equation. If we add to both sides of we get Press the right arrow key or the enter key to advance the slides or

18. EXIT BACK We can now solve this by taking the square root of both sides to get Press the right arrow key or the enter key to advance the slides

19. EXIT BACK is known as the quadratic formula. It is used to solve any quadratic equation in one variable. We will show how the quadratic equation is used in the example that follows. Press the right arrow key or the enter key to advance the slides

20. EXIT BACK First, we start with an equation Then we change it to From this we get Press the right arrow key or the enter key to advance the slides Remember

21. EXIT BACK We then substitute into the quadratic formula, simplify and get our values for . Press the right arrow key or the enter key to advance the slides

22. Remember the quadratic equation is and the values are a = 3, b = 11, c = -20 EXIT BACK Doing so we get Press the right arrow key or the enter key to advance the slides

23. EXIT BACK This gives us two values for , and Press the right arrow key or the enter key to advance the slides

24. EXIT BACK The equation can be factored into which will give us the same solutions as the quadratic formula. However, the beauty of using the quadratic formula is that it works for ALL quadratic equations, even those not factorable (and even when is negative). Press the right arrow key or the enter key to advance the slides

26. EXIT BACK 2. Determine the values of a, b, and c after the equation is set to zero. Press the right arrow key or the enter key to advance the slides Remember

27. EXIT BACK 3. Substitute the values of a, b, and c into the quadratic formula. Press the right arrow key or the enter key to advance the slides

28. EXIT BACK 4. Simplify the formula after substituting and find the solutions. Press the right arrow key or the enter key to advance the slides