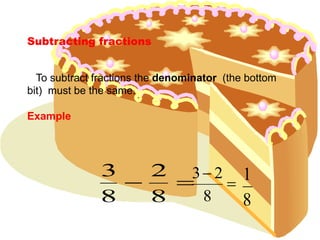
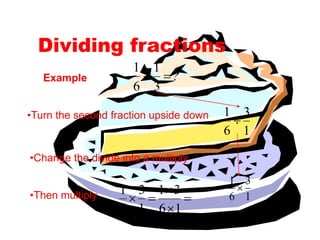
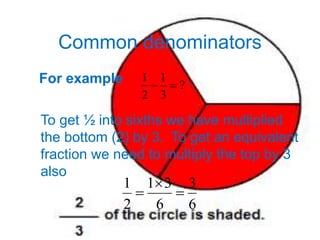
This presentation teaches how to perform operations on fractions, including adding, subtracting, multiplying, and dividing fractions. It explains the key rules for each operation, such as having a common denominator to add or subtract fractions, multiplying the tops and bottoms to multiply fractions, and turning the second fraction upside down and changing division to multiplication for dividing fractions. It also covers how to find common denominators, such as multiplying the denominators together and adjusting the numerators proportionally.

1. FRACTIONS

2. 55/60
Rules of fraction
This presentation will help you to:
• add
• subtract
• multiply and
• divide fractions

3. Subtracting fractions
To subtract fractions the denominator (the bottom
bit) must be the same.
Example

8
2
8
3


8
23
8
1

4. Multiplying fractions
To multiply fractions we multiply the
tops and multiply the bottoms
Top x Top
________________
Bottom x Bottom

5. Dividing fractions
Once you know a simple trick,
dividing is as easy as multiplying!
• Turn the second fraction upside down
• Change the divide to multiply
• Then multiply!

6. Dividing fractions
•Turn the second fraction upside down
Example ?
3
1
6
1
1
3
6
1

•Change the divide into a multiply
1
3
6
1

•Then multiply 



16
31
1
3
6
1

7. Common denominators
To add or subtract fractions together the
denominator (the bottom bit) must be the
same.
So, sometimes we have to change the
bottoms to make them the same.
In “maths-speak” we say we must get
common denominators

8. Common denominators
To get a common denominator we have to:
1. Multiply the bottoms together.
2. Then multiply the top bit by the correct
number to get an equivalent fraction

9. Common denominators
For example ?
3
1
2
1

To get ½ into sixths we have multiplied
the bottom (2) by 3. To get an equivalent
fraction we need to multiply the top by 3
also
6
3
6
31
2
1




10. Common denominators
For example ?
3
1
2
1

To get 1/3 into sixths we have multiplied
the bottom (3) by 2. To get an equivalent
fraction we need to multiply the top by 2
also

11. 1 2/101/12
1/8
1 ½
11/12
55/60
Examples