This document discusses various techniques for frequency estimation from signals. It summarizes maximum likelihood estimation, subspace techniques like MUSIC, the Quinn-Fernandes method, analytic signal generation to enable frequency estimation of real signals, and performance bounds like the Cramér-Rao lower bound. It also mentions Kay's estimator and related weighted frequency estimators that aim to minimize mean square error.

1. Frequency Estimation Techniques Peter J. Kootsookos [email_address]

2. Some acknowledgements What is frequency estimation? What other problems are there? Some algorithms Maximum likelihood Subspace techniques Quinn-Fernandes Associated problems Analytic signal generation Kay / Lank-Reed-Pollon estimators Performance bounds: Cramér-Rao Lower Bound Frequency Estimation Techniques Talk Summary

3. Eric Jacobson – for his presence on comp.dsp and for his work on the topic. Andrew Reilly – for his presence on comp.dsp and for analytic signal advice. Steven M. Kay – for his books on estimation and detection generally, and published research work on the topic. Barry G. Quinn – as a colleague and for his work the topic. I. Vaughan L. Clarkson – as a colleague and for his work on the topic. CRASys – Now defunct Cooperative Research Centre for Robust & Adaptive Systems. Frequency Estimation Techniques Some Acknowledgements

4. Some acknowledgements What is frequency estimation? What other problems are there? Some algorithms Maximum likelihood Subspace techniques Quinn-Fernandes Associated problems Analytic signal generation Kay / Lank-Reed-Pollon estimators Performance bounds: Cramér-Rao Lower Bound Frequency Estimation Techniques Talk Summary

5. Find the parameters A ,  ,   , and  2 in y(t) = A cos [  t-  ) +  )] +  (t) where t = 0..T-1,  T-1/2 and  (t) is a noise with zero mean and variance  2 .  is used to denote the vector [ A    2 ] T . Frequency Estimation Techniques What is frequency estimation?

6. y(t) = A cos [  t-  ) +  )] +  (t) What about A(t) ? Estimating A(t) is envelope estimation (AM demodulation). If the variation of A(t) is slow enough, the problem of estimating  and estimating A(t) decouples. What about  (t) ? This is the frequency tracking problem. What’s  (t) ? Usually assumed additive, white, & Gaussian. Maximum likelihood technique depends on Gaussian assumption. Frequency Estimation Techniques What other problems are there?

7. Amplitude-varying example: condition monitoring in rotating machinery. Frequency Estimation Techniques What other problems are there? [continued]

8. Frequency tracking example: SONAR Frequency Estimation Techniques What other problems are there? [continued] Thanks to Barry Quinn & Ted Hannan for the plot from their book “The Estimation & Tracking of Frequency”.

9. Frequency Estimation Techniques What other problems are there? [continued] Multi-harmonic frequency estimation y(t) =  A m cos [m  t-  ) +  m )] +  (t) For periodic, but not sinusoidal, signals. Each component is harmonically related to the fundamental frequency. p m=1

10. Frequency Estimation Techniques What other problems are there? [continued] Multi-tone frequency estimation y(t) =  A m cos [  m  t-  ) +  m )] +  (t) Here, there are multiple frequency components with no relationship between the frequencies. p m=1

11. Some acknowledgements What is frequency estimation? What other problems are there? Some algorithms Maximum likelihood Subspace techniques Quinn-Fernandes Associated problems Analytic signal generation Kay / Lank-Reed-Pollon estimators Performance bounds: Cramér-Rao Lower Bound Frequency Estimation Techniques Talk Summary

12. The likelihood function for this problem, assuming that  (t) is Gaussian is L(  ) = 1/((2  ) T/2  |R  |) exp(–( Y – Ŷ (  )) T R -1  ( Y – Ŷ (  ))/ 2) where R  = The covariance matrix of the noise  Y = [y(0) y(1) … y(T-1)] T Ŷ = [A cos(  ) A cos(  +  ) … A cos(  (T-1) +  )] T Y is a vector of the date samples, and Ŷ is a vector of the modeled samples. Frequency Estimation Techniques The Maximum Likelihood Approach

13. Two points to note: The functional form of the equation L(  ) = 1/((2  ) T/2  |R  |) exp(–( Y – Ŷ (  )) T R -1  ( Y – Ŷ (  ))/ 2) is determined by the Gaussian distribution of the noise. If the noise is white, then the covariance matrix R is just  2 I – a scaled identity matrix. Frequency Estimation Techniques The Maximum Likelihood Approach [continued]

14. Often, it is easier to deal with the log-likelihood function: ℓ (  ) = –( Y – Ŷ (  ) ) T R -1  ( Y – Ŷ (  ) ) where the additive constant, and multiplying constant have been ignored as they do not affect the position of the peak (unless  is zero or infinite). If the noise is also assumed to be white, the maximum likelihood problem looks like a least squares problem as maximizing the expression above is the same as minimizing ( Y – Ŷ (  ) ) T ( Y – Ŷ (  ) ) Frequency Estimation Techniques The Maximum Likelihood Approach [continued]

15. Frequency Estimation Techniques The Maximum Likelihood Approach [continued] If the complex-valued signal model is used, then estimating  is equivalent to maximizing the periodogram: P(  ) = |  y(t) exp(-i  t) | 2 For the real-valued signal used here, this equivalence is only true as T tends to infinity. t=0 T-1

16. Some acknowledgements What is frequency estimation? What other problems are there? Some algorithms Maximum likelihood Subspace techniques Quinn-Fernandes Associated problems Analytic signal generation Kay / Lank-Reed-Pollon estimators Performance bounds: Cramér-Rao Lower Bound Frequency Estimation Techniques Talk Summary

17. The peak of the spectrum produced by spectral estimators other than the periodogram can be used for frequency estimation. Signal subspace estimators use either P Bar (  ) = v*(  ) R Bar v(  ) or P MV (  ) = 1/( v*(  ) R MV -1 v(  ) ) where v(  ) = [ 1 exp(i  exp(i2  exp(I(T-1)  and an estimate of the covariance matrix is used. Frequency Estimation Techniques Subspace Techniques ^ ^ Note: If R yy is full rank, the P Bar is the same as the periodogram.

18. Bartlett: R Bar =   k e k e* k Minimum Variance: R MV -1 =  1/  k e k e* k Assuming there are p frequency components. Frequency Estimation Techniques Subspace Techniques - Signal ^ ^ k=1 p k=1 p

19. Pisarenko: R Pis -1 = e p+1 e* p+1 Multiple Signal Classification (MUSIC): R MUSIC -1 =  e k e* k Assuming there are p frequency components. Key Idea: The noise subspace is orthogonal to the signal subspace, so zeros of the noise subspace will indicate signal frequencies. Frequency Estimation Techniques Subspace Techniques - Noise ^ ^ M k=p+1 While Pisarenko is not statistically efficient, it is very fast to calculate.

20. The technique of Quinn & Fernandes assumes that the data fits the ARMA(2,2) model: y(t) –  y(t-1) + y(t-2) =  (t) –  (t-1) +  (t-2) Set  1 = 2cos(  ). Filter the data to form z j (t) = y(t) +  j z j (t-1) – z j (t-2) Form  j by regressing ( z j (t) + z j (t-2) ) on z j (t-1)  j =  t  ( z j (t) + z j (t-2) ) z j (t-1) /  t z j 2 (t-1) If |  j -  j | is small enough, set  = cos -1 (  j / 2), otherwise set  j+1 =  j and iterate from 2. Frequency Estimation Techniques Quinn-Fernandes

21. The algorithm can be interpreted as finding the maximum of a smoothed periodogram. Frequency Estimation Techniques Quinn-Fernandes [continued]

22. Some acknowledgements What is frequency estimation? What other problems are there? Some algorithms Maximum likelihood Subspace techniques Quinn-Fernandes Associated problems Analytic signal generation Kay / Lank-Reed-Pollon estimators Performance bounds: Cramér-Rao Lower Bound Frequency Estimation Techniques Talk Summary

23. Other questions that need answering are: What happens when the signal is real-valued, and my frequency estimation technique requires a complex-valued signal? Analytic Signal generation How well can I estimate frequency? Cramer-Rao Lower Bound Threshold performance Frequency Estimation Techniques Associated Problems

24. Many signal processing problems already use “analytic” signals: communications systems with “in-phase” and “quadrature” components, for example. An analytic signal, exp(i-blah) , can be generated from a real-valued signal, cos(blah) , by use of the Hilbert transform: z(t) = y(t) + i H[ y(t) ] where H[.] is the Hilbert transform operation. Problems occur if the implementation of the Hilbert transform is poor. This can occur if, for example, too short an FIR filter is used. Frequency Estimation Techniques Associated Problems: Analytic Signal Generation

25. Another approach is to FFT y(t) to obtain Y(k) . From Y(k) , form Z(k) = 2Y(k) for k = 1 to T/2 - 1 Y(k) for k = 0 0 for k = T/2 to T and then inverse FFT Z(k) to find z(t) . Unless Y(k) is interpolated, this can cause problems. Frequency Estimation Techniques Associated Problems: Analytic Signal Generation [continued] Makes sure the DC term is correct.

26. If you know something about the signal (e.g. frequency range of interest), then use of a band-pass Hilbert transforming filter is a good option. See the paper by Andrew Reilly, Gordon Fraser & Boualem Boashash, “Analytic Signal Generation : Tips & Traps” IEEE Trans. on ASSP, vol 42(11), pp3241-3245 They suggest designing a real-coefficient low-pass filter with appropriate bandwidth using a good FIR filter algorithm (e.g. Remez). The designed filter is then modulated with a complex exponential of frequency f s /4. Frequency Estimation Techniques Associated Problems: Analytic Signal Generation [continued]

27. If an analytic signal, z(t) , is obtained, then the simple relation: arg( z(t+1)z*(t) ) can be used to find an estimate of the frequency at time t. See this by writing: z(t+1)z*(t) = exp(i (  (t+1) +  ) ) exp(-i (  t +  ) ) = exp(i  ) Frequency Estimation Techniques Kay’s Estimator and Related Estimators

28. What Kay did was to form an estimator  = arg( w(t) z(t+1)z*(t) ) where the weights, w(t) , are chosen to minimize the mean square error. Kay found that, for very small noise w(t) = 6t(T-t) / (T(T 2 -1)) which is a parabolic window. Frequency Estimation Techniques Kay’s Estimator and Related Estimators [continued] ^  T-2 t=0

29. If the SNR is known, then it’s possible to choose an optimal set of weights. For “infinite” noise, the rectangular window is best – this is the Lank-Reed-Pollon estimator. The figure shows how the weights vary with SNR. Frequency Estimation Techniques Kay’s Estimator and Related Estimators [continued]

30. The lower bound on the variance of unbiased estimators of the frequency a single tone in noise is var(  ) >= 12  2 / (T(T 2 -1)A 2 ) Frequency Estimation Techniques Associated Problems: Cramer-Rao Lower Bound ^

31. The CRLB for the multi-harmonic case is: var(  ) >= 12  2 / (T(T 2 -1) m 2 A m 2 ) So the effective signal energy in this case is influenced by the square of the harmonic order. Frequency Estimation Techniques Associated Problems: Cramer-Rao Lower Bound [continued] ^  p m=1

32. Frequency Estimation Techniques Associated Problems: Threshold Performance Key idea: The performance degrades when peaks in the noise spectrum exceed the peak of the frequency component. Dotted lines in the figure show the probability of this occurring.

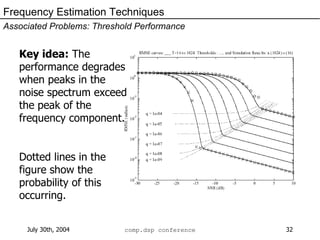
33. Frequency Estimation Techniques Associated Problems: Threshold Performance [continued] For the multi-harmonic case, two threshold mechanisms occur: the noise outlier case and rational harmonic locking. This means that, sometimes, ½, 1/3, 2/3, 2 or 3 times the true frequency is estimated.

34. Some acknowledgements What is frequency estimation? What other problems are there? Some algorithms Maximum likelihood Subspace techniques Quinn-Fernandes Associated problems Analytic signal generation Kay / Lank-Reed-Pollon estimators Performance bounds: Cramér-Rao Lower Bound Frequency Estimation Techniques Talk Summary

35. Thanks to Lori Ann, Al and Rick for hosting and/or organizing this get-together. Frequency Estimation Techniques Thanks!

36. Frequency Estimation Techniques Good-bye!