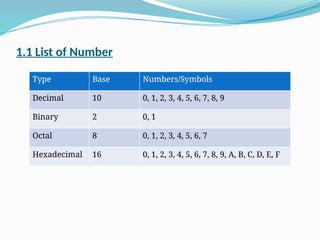
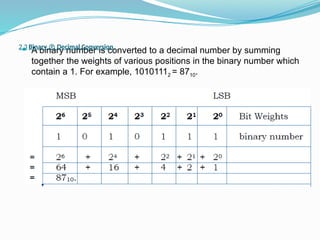
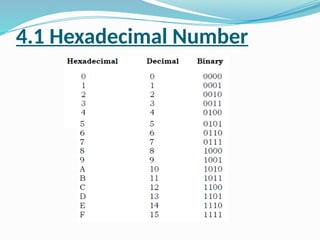
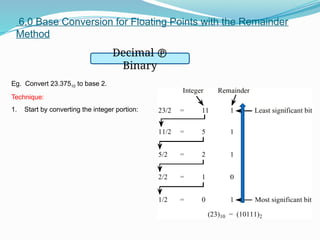
This document covers number systems and codes, focusing on binary, octal, hexadecimal, and binary-coded decimal (BCD) systems. It details conversion methods between these systems, explaining how to convert numbers from one base to another using various techniques. Additionally, it includes exercises for practice on converting numbers in different formats.

1. CHAPTER 1 :NUMBER SYSTEMS
AND CODES
Objectives :
•Binary, Octal, Hexadecimal and BCD Number System.
• Number Conversion

2. Outcomes
 At the end of this chapter, students should be
able to:-
 Differentiate between decimal, binary, octal,
hexadecimal and BCD.
 Convert number between bases.

3. 1.0 Types of Number System
Numbe
r
System
s
Decima
l
Binary
Octal
Hexa
decimal

4. 1.1 List of Number
Type Base Numbers/Symbols
Decimal 10 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Binary 2 0, 1
Octal 8 0, 1, 2, 3, 4, 5, 6, 7
Hexadecimal 16 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

5. 2.0 Binary Numbers
 Used to represent the voltage levels of a digital circuit.
 Only two voltage levels present in a digital circuit, logic High and
logic Low.
 The high voltage is +5V and the low voltage is +0V.
 The binary numbers represent the logic low as a 0 and the logic high
as a 1.

6.  A calculator is an example of a digital system.
 Decimal numbers are pressed on the keypad, where the input values
are converted to binary for processing, then converts the answers to
a decimal value before displaying them.
 Number conversion occurs extensively in a digital circuit.
 In this chapter, you will learn numbers systems and codes used in
digital circuit. You will also learn how to perform conversion from one
number system to another.
2.1 Binary Numbers Example

7.  A decimal number can be converted to a binary number by
successively dividing the number by 2 as follows:
•Note that the first remainder becomes the most significant bit (MSB). The last
remainder becomes the least significant bit (LSB).
2.2 Decimal  Binary Conversion

8.  A binary number is converted to a decimal number by summing
together the weights of various positions in the binary number which
contain a 1. For example, 10101112 = 8710.
2.3 Binary  Decimal Conversion

9. 3.0 Decimal  Octal Conversion
 A decimal number can be converted to an octal number by
successively dividing the number by 8 as follows:
266 ÷ 8 = 33 remainder 2 LSD (right-most digit)
33 ÷ 8 = 4 remainder 1
4 ÷ 8 = 0 remainder 4 MSB (left-most digit).
 Therefore 26610 = 4128

10.  To convert an octal number to a decimal number, multiply each octal
value by the weight of the digit and sum the results. For example,
4128 = 26610.
3.1 Octal  Decimal Conversion

11.  Each octal digit can be represented by a 3-bit binary number as
shown below:
3.2 Octal  Binary Representation

12.  Conversion from octal to binary is very straightforward. Each octal digit
is replaced by 3-bit binary number. For example, 4728 = 100 111 0102.
 A binary number is converted into an octal number by taking groups of
3 bits, starting from LSB, and replacing them with an octal digit. For
example, 11 010 1102 = 3268
.
3.3 Octal Binary Conversion

13. 4.0 Hexadecimal Number
 The hexadecimal number uses base 16. It uses the digits 0 through
9 plus the letters A, B, C, D, E and F.
 The letter A stands for decimal 10, B for 11, C for 12, D for 13, E for
14 and F for 15.

14. 4.1 Hexadecimal Number

15.  A decimal number can be converted to hex number by successively
dividing the number by 16 as follows:
4.2 Decimal  Hexadecimal Conversion

16.  To convert a hex number to a decimal number, multiply each hex
value by the weight of the digit and sum the results. For example,
1A716 = 42310.
4.3 Hexadecimal  Decimal Conversion

17.  Each hex digit can be represented by a 4-bit binary number as
shown above. Conversion from hex to binary is very straightforward.
Each hex digit is replaced by 4-bit binary number.
 A binary number is converted into an octal number by taking groups
of 4 bits, starting from LSB, and replacing them with a hex digit. For
example, 110101102 = 3268
.
4.4 Hexadecimal Binary Conversion

18. 5.0 Binary-Coded-Decimal (BCD)
 Conversions between decimal and binary can become long and
complicated for large numbers.
 For example, convert 87410 to binary. The answer is 11011010102,
but it takes quite a lot of time and effort to make this conversion. We
call this straight binary coding.

19. 5.1 Binary-Coded-Decimal (BCD)
 The Binary-Coded-Decimal (BCD) code makes conversion much
easier. Each decimal digit, 0 through 9, is represented with a 4-Bit
BCD code as shown below. The BCD code 1010, 1011, 1100, 1101,
1110 and 1111 are not used.

20.  Conversion between BCD and decimal is accomplished by replacing
a 4-bit BCD for each decimal digit. For example, 87410 = 1000 0111
0100BCD.
 BCD is not another number system like binary, octal, decimal and
hexadecimal. It is in fact the decimal system with each digit encoded
in its binary equivalent. A BCD code is not the same as a straight
binary number. For example, the BCD code requires 12 bits, while
the straight binary number requires only 10 bits to represent 87310.
5.2 Decimal  BCD Conversion

21.  A BCD code is converted into a decimal number by taking groups of
4 bits, starting from LSB, and replacing them with a BCD code. For
example, 1 1001 0111 1000 BCD = 197810
5.3 BCD  Decimal Conversion

22. Exercises
1. Convert decimal 23410 to
a. binary
b. BCD
b. octal
c. hexadecimal
2. Convert binary 10010111012 to
a. decimal
b. octal
c. hexadecimal
d. BCD

23. 3. Convert hexadecimal ABF216 to
a. decimal
b. binary
c. octal
d. BCD
4. Convert BCD 10010100100110001BCD to
a. decimal
b. octal
c. hexadecimal
d. binary
5. Convert number octal 5268 to
a. decimal
b. BCD
c. hexadecimal
d. binary
Exercises

24. 6.0 Base Conversion for Floating Points with the Remainder
Method
Decimal 
Binary
Eg. Convert 23.37510 to base 2.
Technique:
1. Start by converting the integer portion:

25. 6.0 Floating Points Conversion using Remainder Method
Decimal 
Binary
2. Then, convert the fraction by multiply it with the based we want to convert:
IF ZERO, THEN STOP

26. 6.0 Base Conversion for Floating Points with the Remainder
Method
Eg. 1010.012 = _________ 10
 Technique:
– Multiply each binary number by 2-n
, where -n is the weight of the bit for fraction starting from left to
right. .
– Then, sum the results.
1010.012
= 1 x 23
+ 0 x 22
+ 1 x 21
+ 0 x 20
. 0 x 2-1
+ 1 x 2-2
= 10 + 0.25
= 10.25 10
Therefore, 1010.012 = 10.2510
Binary  Decimal

27. 6.0 Base Conversion for Floating Points with the Remainder
Method
Octal – Decimal
Technique:
– Multiply each octal number by 8-n
, where -n is the weight of the bit for
fraction starting from left to right. .
– Then, sum the results.
Eg. 46.38 = _________10
46.38 = 4 x 81
+ 6 x 80
+ 3 x 8-1
= 38 + 0.375
= 38.37510
Therefore, 46.38 = 38.37510

28. 6.0 Base Conversion for Floating Points with the Remainder
Method
Hexadecimal -
Decimal
Technique:
– Multiply each hexadecimal number by 16-n
, where -n is the weight of the bit
for fraction starting from left to right.
– Then, sum the results.
Eg. A7.0F16 = _________10
A7.0F16 = 10 x 161
+ 7 x 160
+ 0 x 16-1
+ 15 x 16-2
= 167 + 0.059
= 167.05910
Therefore, A7.0F16 = 167.05910

29. Exercises
1. Convert the following number to the indicated base/code.
a) 11101.112 to decimal.
b) FED.4716 to octal.
c) 01101001BCD to binary.
d) 7548 to BCD.
e) 152.2510 to hexadecimal.