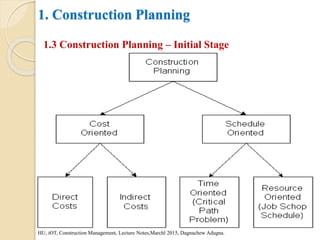
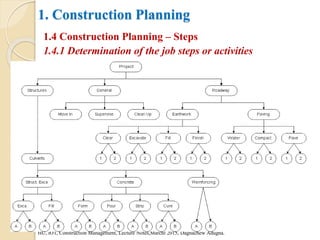
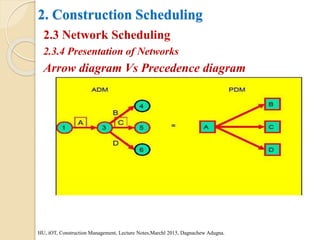
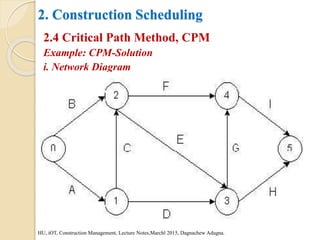
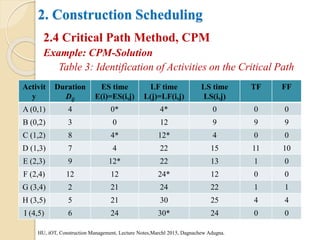
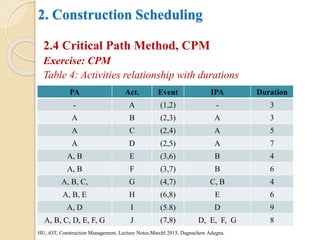
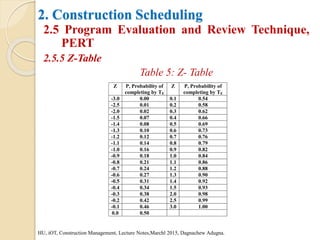
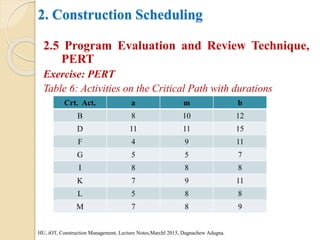
This document provides an overview of construction planning and scheduling. It discusses the importance of construction planning, including the advantages of planning before, during, and after a project's completion. It also outlines the steps involved in construction planning, including determining activities, sequencing activities, estimating activity durations, and developing schedules. The document also discusses construction scheduling techniques like bar charts, network scheduling using critical path method (CPM) and program evaluation review technique (PERT), and how to calculate critical paths.