This document contains examples of calculating principal values of inverse trigonometric functions. It includes solving equations involving inverse trigonometric functions and proving trigonometric identities related to inverse functions. The document provides step-by-step workings for 17 questions involving inverse sine, cosine, tangent, cotangent, secant and cosecant functions, demonstrating how to determine principal values from given ranges and simplify expressions involving inverse trig functions.

1. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 1 of 38
Exercise 2.1
Question 1:
Find the principal value of
Answer
Let sin-1
Then sin y =
We know that the range of the principal value branch of sin−1
is
and sin
Therefore, the principal value of
Question 2:
Find the principal value of
Answer
We know that the range of the principal value branch of cos−1
is
.
Therefore, the principal value of .
Question 3:
Find the principal value of cosec−1
(2)
Answer

2. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 2 of 38
Let cosec−1
(2) = y. Then,
We know that the range of the principal value branch of cosec−1
is
Therefore, the principal value of
Question 4:
Find the principal value of
Answer
We know that the range of the principal value branch of tan−1
is
Therefore, the principal value of
Question 5:
Find the principal value of
Answer
We know that the range of the principal value branch of cos−1
is
Therefore, the principal value of

3. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 3 of 38
Question 6:
Find the principal value of tan−1
(−1)
Answer
Let tan−1
(−1) = y. Then,
We know that the range of the principal value branch of tan−1
is
Therefore, the principal value of
Question 7:
Find the principal value of
Answer
We know that the range of the principal value branch of sec−1
is
Therefore, the principal value of
Question 8:
Find the principal value of
Answer

4. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 4 of 38
We know that the range of the principal value branch of cot−1
is (0,π) and
Therefore, the principal value of
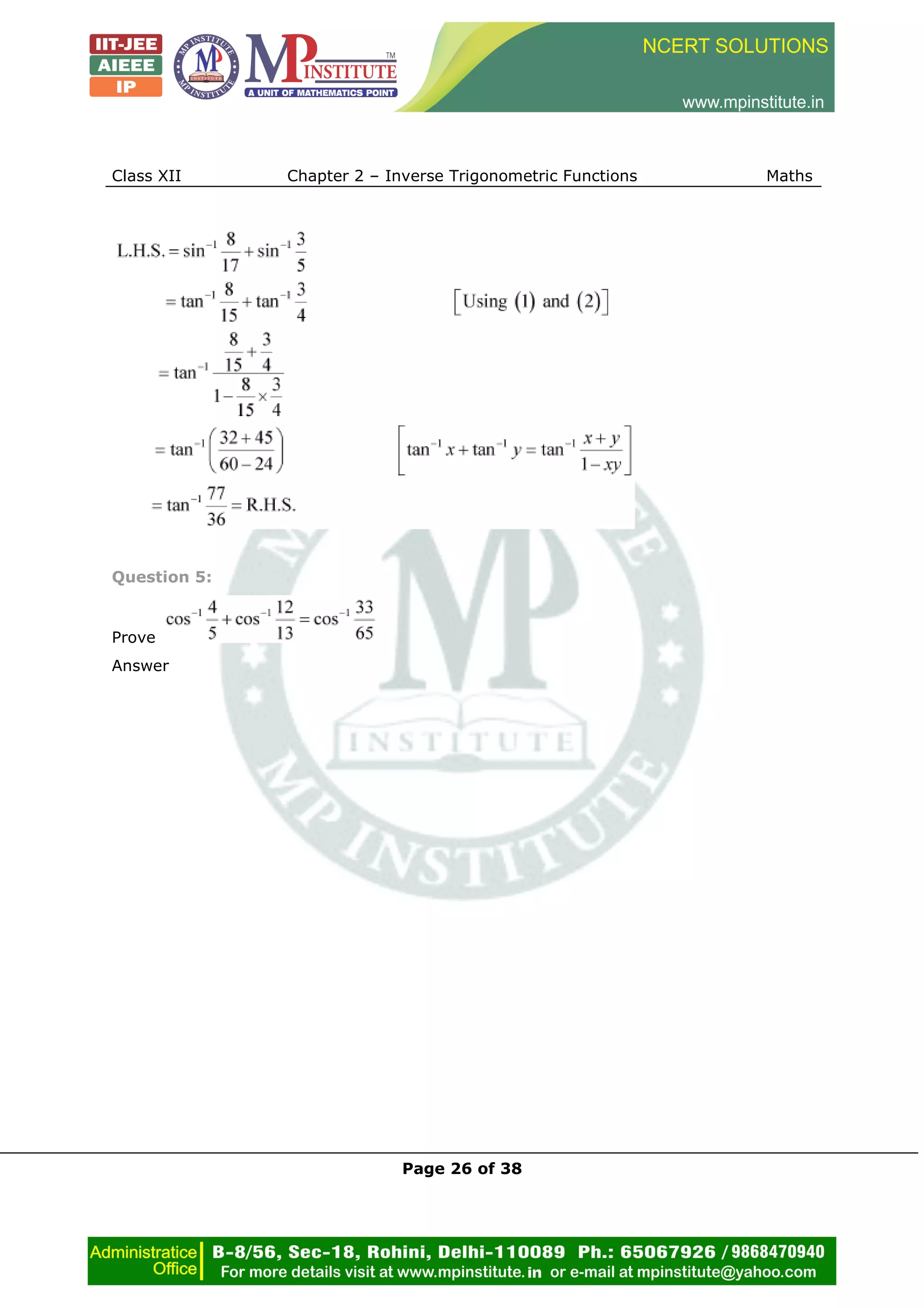
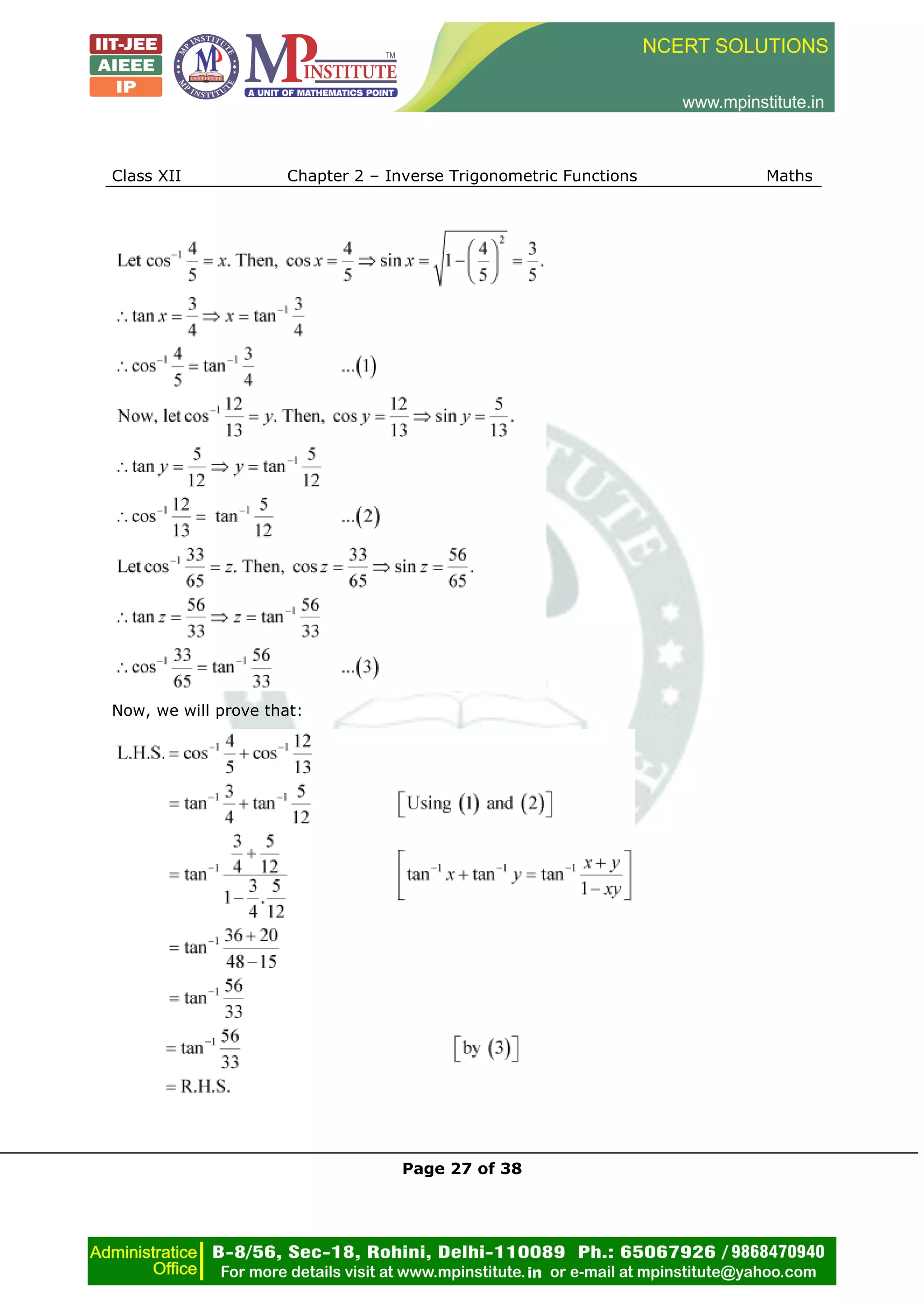
Question 9:
Find the principal value of
Answer
We know that the range of the principal value branch of cos−1
is [0,π] and
.
Therefore, the principal value of
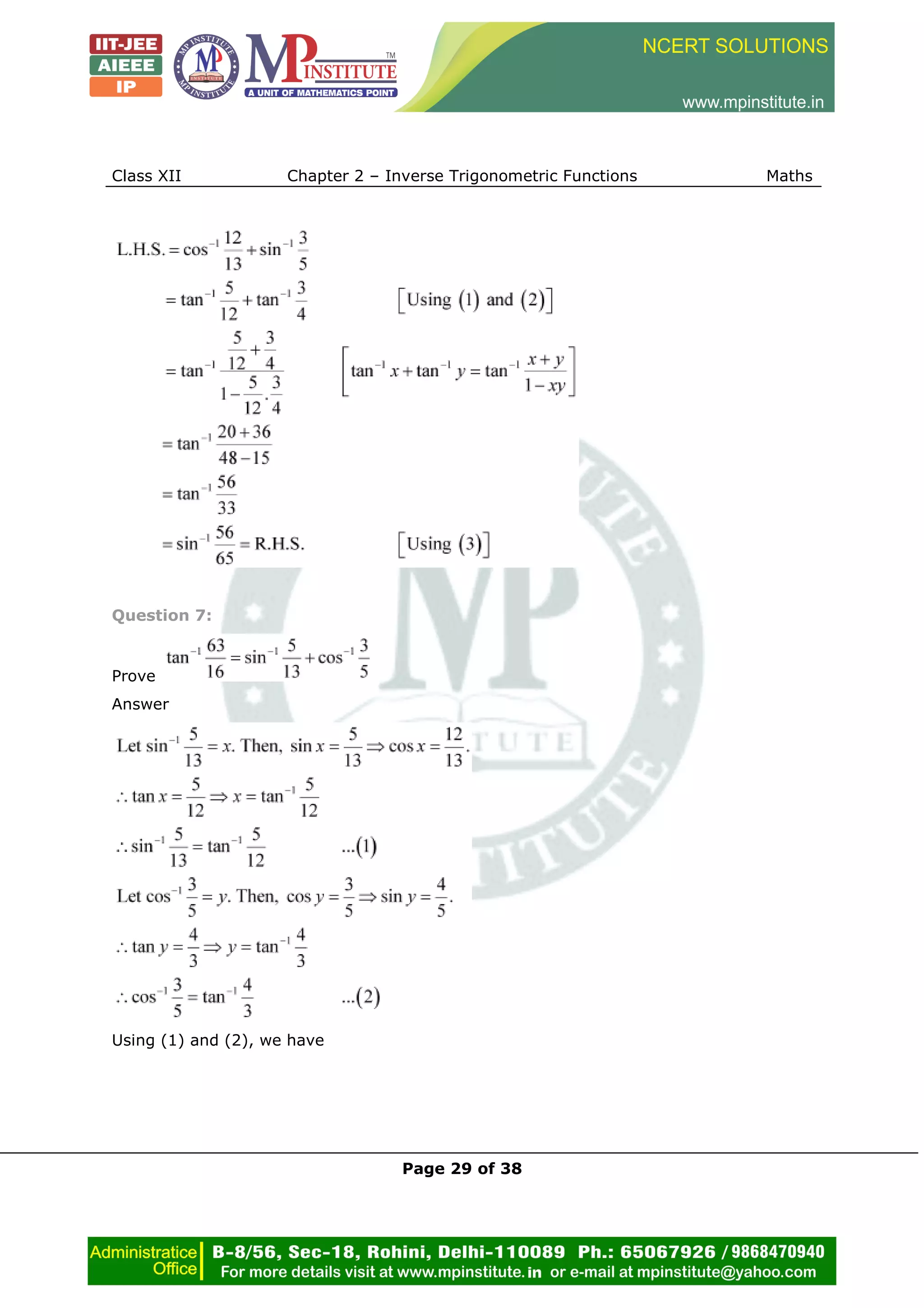
Question 10:
Find the principal value of
Answer
We know that the range of the principal value branch of cosec−1
is
Therefore, the principal value of

5. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 5 of 38
Question 11:
Find the value of
Answer
Question 12:
Find the value of
Answer

6. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 6 of 38
Question 13:
Find the value of if sin−1
x = y, then
(A) (B)
(C) (D)
Answer
It is given that sin−1
x = y.
We know that the range of the principal value branch of sin−1
is
Therefore, .
Question 14:
Find the value of is equal to
(A) π (B) (C) (D)
Answer

7. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 7 of 38

8. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 8 of 38
Exercise 2.2
Question 1:
Prove
Answer
To prove:
Let x = sinθ. Then,
We have,
R.H.S. =
= 3θ
= L.H.S.
Question 2:
Prove
Answer
To prove:
Let x = cosθ. Then, cos−1
x =θ.
We have,

9. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 9 of 38
Question 3:
Prove
Answer
To prove:
Question 4:
Prove
Answer
To prove:

10. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 10 of 38
Question 5:
Write the function in the simplest form:
Answer

11. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 11 of 38
Question 6:
Write the function in the simplest form:
Answer
Put x = cosec θ ⇒ θ = cosec−1
x
Question 7:
Write the function in the simplest form:

12. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 12 of 38
Answer
Question 8:
Write the function in the simplest form:
Answer

13. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 13 of 38
Question 9:
Write the function in the simplest form:
Answer
Question 10:
Write the function in the simplest form:
Answer

14. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 14 of 38
Question 11:
Find the value of
Answer
Let . Then,
Question 12:

15. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 15 of 38
Find the value of
Answer
Question 13:
Find the value of
Answer
Let x = tan θ. Then, θ = tan−1
x.
Let y = tan Φ. Then, Φ = tan−1
y.
Question 14:

16. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 16 of 38
If , then find the value of x.
Answer
On squaring both sides, we get:

17. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 17 of 38
Hence, the value of x is
Question 15:
If , then find the value of x.
Answer

18. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 18 of 38
Hence, the value of x is
Question 16:
Find the values of
Answer

19. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 19 of 38
We know that sin−1
(sin x) = x if , which is the principal value branch of
sin−1
x.
Here,
Now, can be written as:
Question 17:
Find the values of
Answer
We know that tan−1
(tan x) = x if , which is the principal value branch of
tan−1
x.
Here,
Now, can be written as:

20. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 20 of 38
Question 18:
Find the values of
Answer
Let . Then,
Question 19:

21. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 21 of 38
Find the values of is equal to
(A) (B) (C) (D)
Answer
We know that cos−1
(cos x) = x if , which is the principal value branch of cos
−1
x.
Here,
Now, can be written as:
The correct answer is B.
Question 20:
Find the values of is equal to
(A) (B) (C) (D) 1
Answer
Let . Then,
We know that the range of the principal value branch of .

22. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 22 of 38
∴
The correct answer is D.

23. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 23 of 38
Miscellaneous Solutions
Question 1:
Find the value of
Answer
We know that cos−1
(cos x) = x if , which is the principal value branch of cos
−1
x.
Here,
Now, can be written as:
Question 2:
Find the value of
Answer
We know that tan−1
(tan x) = x if , which is the principal value branch of
tan −1
x.
Here,
Now, can be written as:

24. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 24 of 38
Question 3:
Prove
Answer
Now, we have:

25. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 25 of 38
Question 4:
Prove
Answer
Now, we have:

26. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 26 of 38
Question 5:
Prove
Answer

27. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 27 of 38
Now, we will prove that:

28. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 28 of 38
Question 6:
Prove
Answer
Now, we have:

29. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 29 of 38
Question 7:
Prove
Answer
Using (1) and (2), we have

30. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 30 of 38
Question 8:
Prove
Answer

31. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 31 of 38
Question 9:
Prove
Answer

32. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 32 of 38
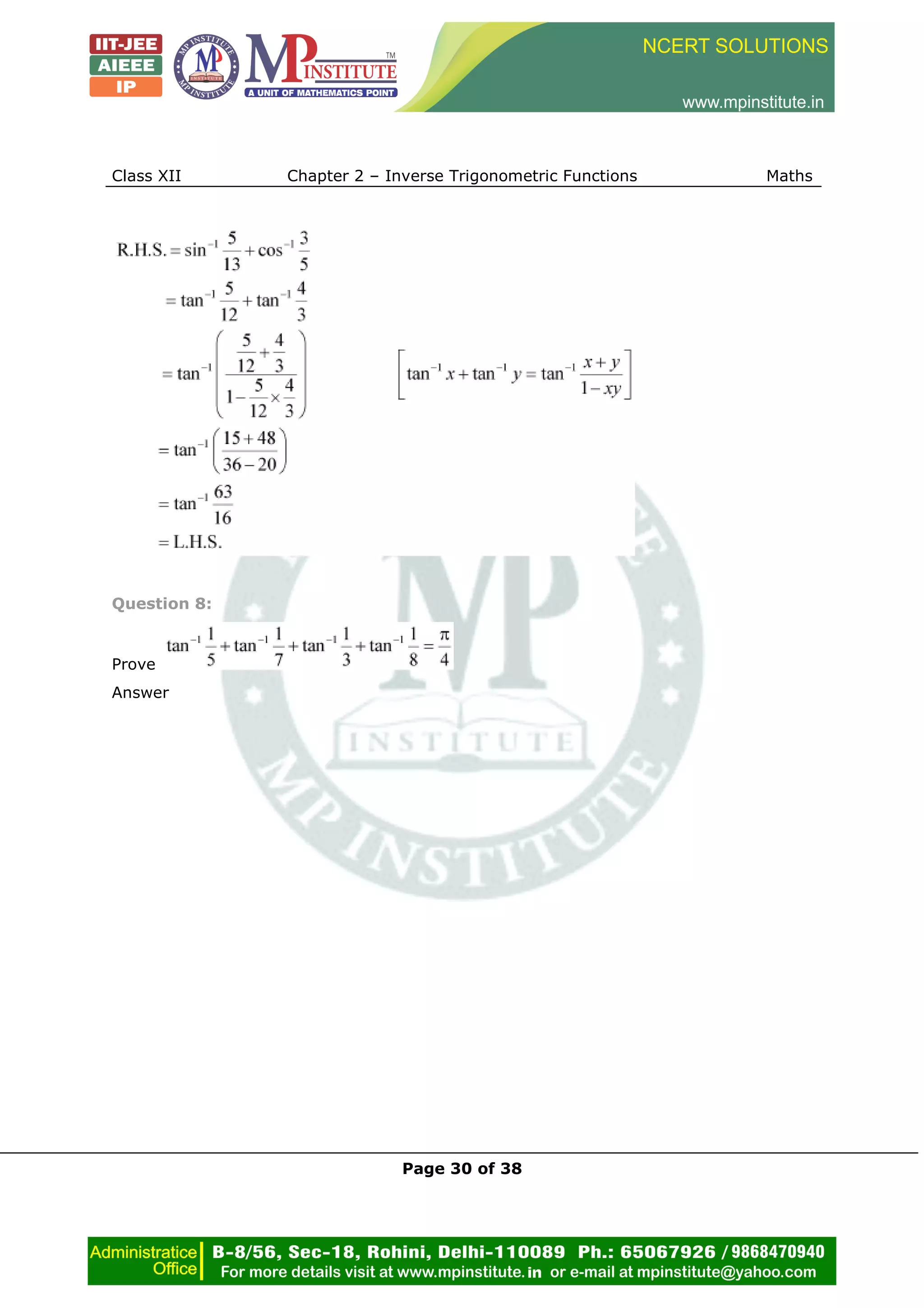
Question 10:
Prove
Answer
Question 11:
Prove [Hint: putx = cos 2θ]
Answer

33. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 33 of 38
Question 12:
Prove
Answer

34. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 34 of 38
Question 13:
Solve
Answer
Question 14:
Solve
Answer

35. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 35 of 38
Question 15:
Solve is equal to
(A) (B) (C) (D)
Answer
Let tan−1
x = y. Then,
The correct answer is D.
Question 16:
Solve , then x is equal to

36. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 36 of 38
(A) (B) (C) 0 (D)
Answer
Therefore, from equation (1), we have
Put x = sin y. Then, we have:
But, when , it can be observed that:

37. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 37 of 38
is not the solution of the given equation.
Thus, x = 0.
Hence, the correct answer is C.
Question 17:
Solve is equal to
(A) (B). (C) (D)
Answer

38. Class XII Chapter 2 – Inverse Trigonometric Functions Maths
Page 38 of 38
Hence, the correct answer is C.