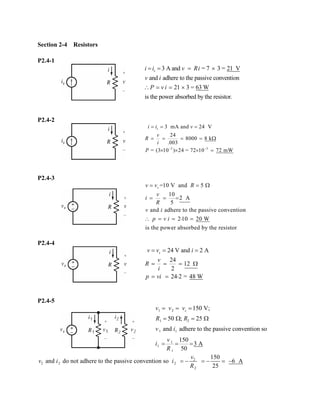
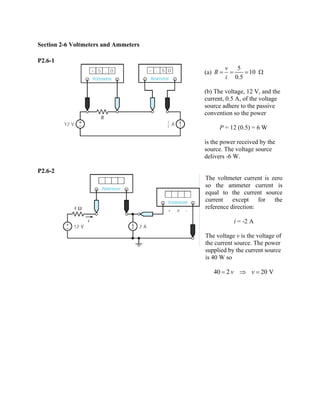
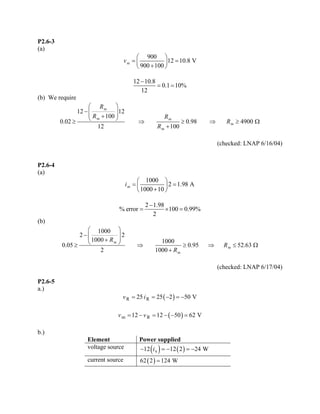
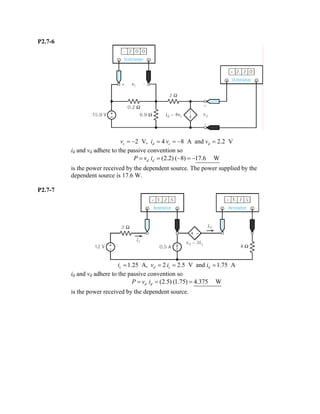
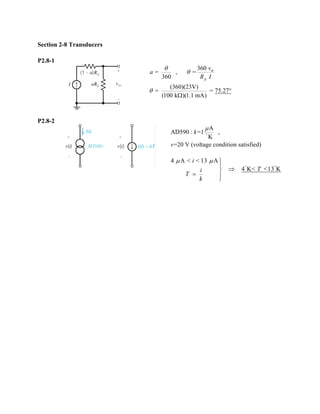
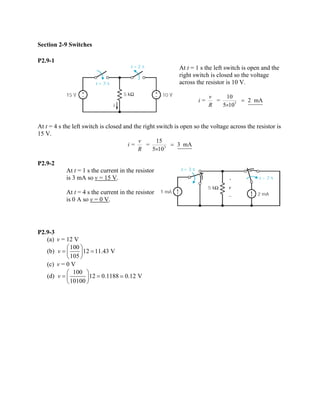
The document contains solutions to practice problems related to linear and nonlinear circuit elements, resistors, independent and dependent sources, transducers, switches, and measurement techniques. In problem P2.2-1, an element is found to be nonlinear because doubling the current does not double the voltage. In problem P2.4-1, the power absorbed by a resistor is calculated to be 21V×3A=63W. In problem P2.6-1, the power received by a voltage source is calculated to be 12V×0.5A=6W, with the source delivering -6W.

1. Problems
Section 2-2 Engineering and Linear Models
P2.2-1
The element is not linear. For example, doubling the current from 2 A to 4 A does not double the voltage. Hence, the property of homogeneity is not satisfied.
P2.2-2
(a) The data points do indeed lie on a straight line. The slope of the line is 0.12 V/A and the line passes through the origin so the equation of the line is 0.12v=. The element is indeed linear.
(b) When i = 40 mA, v = (0.12 V/A)×(40 mA) = (0.12 V/A)×(0.04 A) = 4.8 mV
(c) When v = 4 V, 433.3A0.12i==
P2.2-3
(a) The data points do indeed lie on a straight line. The slope of the line is 256.5 V/A and the line passes through the origin so the equation of the line is 256.5v=. The element is indeed linear.
(b) When i = 4 mA, v = (256.5 V/A)×(4 mA) = (256.5 V/A)×(0.004 A) = 1.026 V
(c) When v = 12 V, 120.04678256.5i== A = 46.78 mA.
P2.2-4
Let i = 1 A , then v = 3i + 5 = 8 V. Next 2i = 2A but 16 = 2v ≠ 3(2i) + 5 = 11.. Hence, the property of homogeneity is not satisfied. The element is not linear.
P2.2-5
(a) 0.4 3.2 V10408vvvv=+=⇒= 0.08 A40vi==
(b) 220.4 0.801025vvvv=+⇒+−=
Using the quadratic formula 0.21.80.8, 1.0 V2v−± ==−
When v = 0.8 V then 20.80.32 A2i==. When v = -1.0 V then ()210.5 A2i− ==.

2. (c) 220.40.8 0.801025vvvv=++⇒++=
Using the quadratic formula 0.20.043.22v−±− =
So there is no real solution to the equation.

3. Section 2-4 Resistors
P2.4-1 3 A and = 7 3 = 21 Vand adhere to the passive convention 21 3 = 63 W is the power absorbed by the resistor. siivRiviPvi===×∴==×
P2.4-2 333 mA and 24 V24 8000 8 k.003= (310)24 = 7210 72 mWsiivvRiP−− === ====Ω×××=
P2.4-3 =10 V and 5 10 2A5and adhere to the passive convention 210 20 Wis the power absorbed by the resistorsvvRviRvipvi==Ω=== ∴==⋅=
P2.4-4 24V and 2 A24 122 242 = 48 WsvvivRipvi=== ===Ω==⋅
P2.4-5 121211111 150 V; 50 ; 25 and adhere to the passive convention so 150 3 A50svvvRRviviR=== =Ω=Ω=== 22222150 and do not adhere to the passive convention so 6 A25vviiR=−=−=−

4. 1111The power absorbed by is 1503450 WRPvi==⋅= 2 2 2 2The power absorbed by is 150(6) 900 WRPvi=−=−−=
P2.4-6 1 2 12 1 1 1 1 1 1 1 1 12 A ; =4 and 8 and do not adhere to the passive convention so 428 V. The power absorbed by is (8)(2) 16 W. siiiRRvivRiRPvi=== Ω=Ω=−=−⋅=− =−=−−= 2 22 2 2 2 2 2 2 and do adhere to the passive convention so 82 16 V . The power absorbed by 16232 W. vivRiRisPvi==⋅= ==⋅=
P2.4-7 22222Model the heater as a resistor, then(250)with a 250 V source: 62.51000(210)with a 210 V source: 705.6 W62.5vvPRRPvPR=⇒=== ===
P2.4-8 2225000125The current required by the mine lights is: A1203Power loss in the wire is : Thus the maximum resistance of the copper wire allowed is 0.050.055000 0.144 (125/3) now PiviRPRi=== ×===Ω662since the length of the wire is 2100 200 m 20,000 cmthus / with = 1.710cm from Table 2.511.71020,000 0.236cm0.144LRLALAR ρρρ − − =×== =×Ω⋅ ××===

5. *P2.4-9 3804200.78840.810810238098420gain=≤≤= ++ 0.78840.81080.79962nominalgain+ == 0.79960.78840.81080.7996 1001001.40% 0.79960.7996gaintolerance−− =×=×
So
0.79961.40%gain=±
P2.4-10
Label the current i as shown. That current is the element current in both resistors. First a40vi=
Next abba4040vvvRiRRv==⇒=
For example, 7.054024 11.75R==

6. Section 2-5 Independent Sources
P2.5-1
(a) ()2215 3 A and 53 45 W5sviPRiR======
(b) and do not depend on .siPi The values of and are 3 A and 45 W, both when 3 A and when 5 A.ssiPii==
P2.5-2
(a) 22 10 5210 V and 20 W5svvRiPR==⋅====
(b) and do not depend on . svPv
The values of and are 10V and 20 W both when 10 V and when 5 VssvPvv==
P2.5-3 Consider the current source: and do not adhere to the passive convention, so 312 36 W is the power supplied by the current source. sscsssivPiv==⋅= Consider the voltage source: and do adhere to the passive convention, so 312 36 W is the power absorbed by the voltage source. The voltage source supplies 36 W. ssvsssivPiv==⋅= ∴−
P2.5-4 Consider the current source: and adhere to the passive conventionso 312 36 W is the power absorbed by the current source. Current source supplies 36 W. sscsssivPiv==⋅= − Consider the voltage source: and do not adhere to the passive convention so 31236 W is the power supplied by the voltage source. ssvsssivPiv==⋅=

7. P2.5-5
(a) 2(2 cos ) (10 cos )20 cos mWPvittt===
(b) 111200011 20 cos =20sin2105 sin 2 mJ 24 wPdttdttt⎛⎞==+=+⎜⎟ ⎝⎠∫∫
P2.5-6
(a) capacity800 mAhtime to discharge 16 hourscurrent50 mA===

8. Section 2-6 Voltmeters and Ammeters
P2.6-1
(a) 5100.5vRi===
(b) The voltage, 12 V, and the current, 0.5 A, of the voltage source adhere to the passive convention so the power
P = 12 (0.5) = 6 W
is the power received by the source. The voltage source delivers -6 W.
P2.6-2
The voltmeter current is zero so the ammeter current is equal to the current source current except for the reference direction:
i = -2 A
The voltage v is the voltage of the current source. The power supplied by the current source is 40 W so
40220 Vvv=⇒=

9. P2.6-3
(a) m9001210.8 V900100v⎛⎞==⎜⎟+⎝⎠ 1210.80.110% 12− ==
(b) We require mmmmm12121000.02 0.98 4900 12100RRRRR⎛⎞ −⎜⎟⎜⎟+⎝⎠≥⇒≥⇒ +
(checked: LNAP 6/16/04)
P2.6-4
(a) m100021.98 A100010i⎛⎞==⎜⎟+⎝⎠ 21.98% error1000.99% 2− =×=
(b) mmm100022100010000.05 0.95 52.63 21000RRR⎛⎞ −⎜⎟⎜⎟+⎝⎠≥⇒≥⇒ +
(checked: LNAP 6/17/04)
P2.6-5
a.)
()RR2525250 Vvi==−=−
()mR12125062 Vvv=−=−−=
b.)
Element
Power supplied
voltage source
()()s1212224 Wi−=−=−
current source
()622124 W=

10. resistor
()()RR502100 Wvi−×=−−−=−
total
0
P2.6-6
a.) RR120.48 A2525vi===
mR20.4821.52 Aii=−=−=−
b.)
Element
Power supplied
voltage source
()()m12121.5218.24 Wi=−=−
current source
()()s2122=24 Wv=
resistor
()()RR120.485.76 Wvi−×=−=−
total
0

11. Section 2-7 Dependent Sources
P2.7-1 842bavri===Ω
P2.7-2 2 A8 V ; 2 A ; 0.25 8Vabbabivgvigv ======
P2.7-3 32A 8 A ; 32A ; 4 8Aabbabiidiidi======
P2.7-4 8V2 V ; 8 V ; 4 2Vbaabavvbvvbv======
P2.7-5 42 2R=−=Ω− and 2V4 0.5AA==− −
(checked: LNAP 6/6/04)

12. P2.7-6
2 V, 48 A and 2.2 Vcdcdvivv=−==−=
id and vd adhere to the passive convention so (2.2)(8)17.6 WddPvi==−=−
is the power received by the dependent source. The power supplied by the dependent source is 17.6 W.
P2.7-7
1.25 A, 22.5 V and 1.75 Acdcdivii====
id and vd adhere to the passive convention so (2.5)(1.75)4.375 WddPvi===
is the power received by the dependent source.

13. Section 2-8 Transducers
P2.8-1 360 = , = 360(360)(23V)= =75.27(100 k)(1.1 mA) mpvaRI θθθ° Ω
P2.8-2 AAD590 : =1 , K=20 V (voltage condition satisfied) kv μ ° 4 A<<13 A4K< <13K iTiTk μμ °° ⎫⎪ ⇒⎬ =⎪⎭

14. Section 2-9 Switches
P2.9-1
At t = 1 s the left switch is open and the right switch is closed so the voltage across the resistor is 10 V. 310= = 2mA510viR= ×
At t = 4 s the left switch is closed and the right switch is open so the voltage across the resistor is 15 V. 315= = 3mA510viR= ×
P2.9-2
At t = 1 s the current in the resistor is 3 mA so v = 15 V.
At t = 4 s the current in the resistor is 0 A so v = 0 V.
P2.9-3
(a) v = 12 V
(b) 1001211.43 V105v⎛⎞==⎜⎟ ⎝⎠
(c) v = 0 V
(d) 100120.11880.12 V10100v⎛⎞==⎜⎟ ⎝⎠

15. Section 2-10 How Can We Check…?
P2.10-1 =40 V and =(2)2 A. (Notice that the ammeter measures rather than .) 40V So 202AYour lab partner is wrong. osssosviivi−−=− ==
P2.10-2 12We expect the resistor current to be =0.48 A. The power absorbed by25this resistor will be = (0.48) (12) = 5.76 W. A half watt resistor can't absorb this much power. You should nssviRPiv== = ot try another resistor.