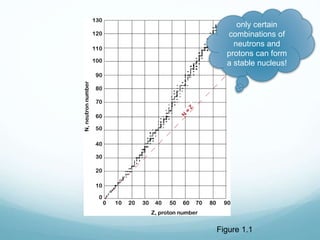
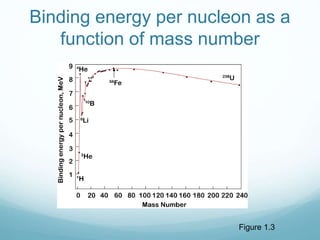
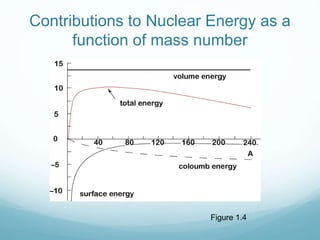
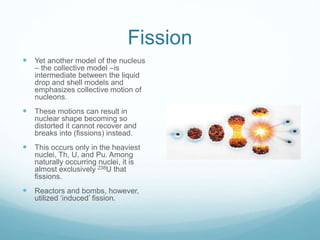
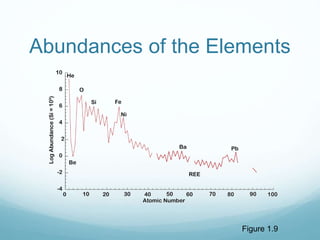
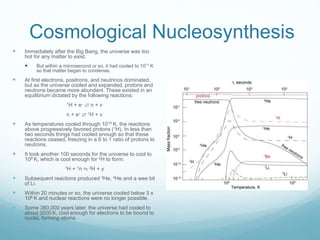
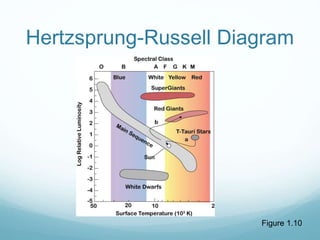
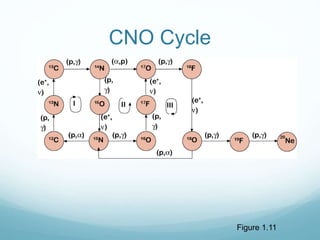
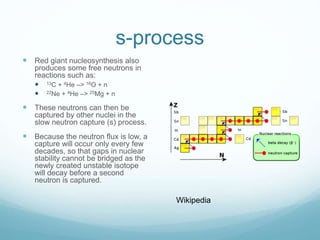
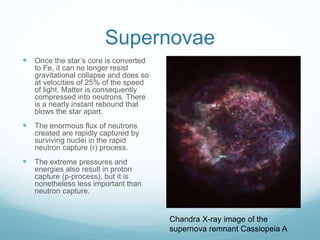
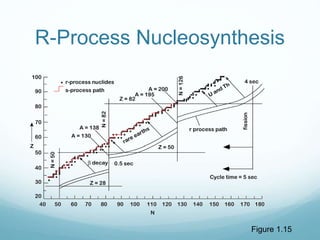
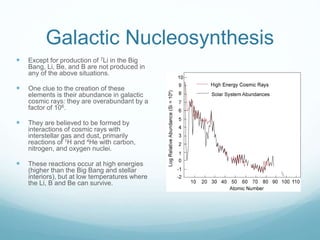
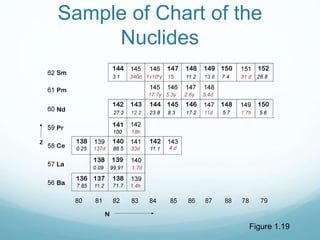
Isotope geochemistry can be used for geochronology, understanding solar system and continent evolution, tracing the history of life, unraveling climate history, and determining the origin of mineral and energy resources. The history of isotope geochemistry began with the discovery of radioactivity and production of the first radiometric age for the Earth. Isotopes have differing numbers of neutrons. Nuclear stability depends on the balance of nuclear forces. Radioactive decay follows exponential laws. Isotope ratios are altered by geological processes and can be used to study earth systems. Stable and radioactive isotopes are produced via stellar nucleosynthesis during the lives of stars and their deaths as supernovae.

2. Isotope Geochemistry
 Some things we can do with it
 Geochronology: Putting a time scale on Earth history
 Understanding the formation of the solar system planets
 Tracing the evolution of continents
 Tracing the history of life
 Unraveling climate history
 Including paleotemperatures
 Origin of mineral and energy resources
 including temperatures of ore-forming fluids

3. History
 History of isotope geochemistry
begins with Bacquerel’s discovery
of radioactivity.
 Within a decade, Bertram
Boltwood of Yale produced the
first ‘radiometric’ age, showing the
Earth was far older than physicists
had thought.
 A few years later, J. J. Thompson
showed the existence of isotopes
(of neon).
 Harold Urey developed a
quantitative theory of isotope
fractionation in 1947.
Henri Bacquerel

4. Protons, Neutrons, and Nuclei
 Constituents of Atoms:
 proton: 1.007276467 u = 1.67262178 × 10-27 kg = 938.2720 MeV/c2
 neutron 1.008664916 u
 electron 0.0005485799 u = 9.10938291 x 10-31 kg = 0.5109989 MeV/c2
 Definitions
 N: the number of neutrons
 Z: the number of protons (same as atomic number since the number of protons
dictates the chemical properties of the atom)
 A: Mass number (N + Z)
 M: Atomic Mass, I: Neutron excess number (I = N – Z)
 Isotopes have the same number of protons but different numbers of neutrons
 Isobars have the same mass number (N + Z), but N and Z are different
 Isotones have the same number of neutrons but different number of protons.

5. Figure 1.1
only certain
combinations of
neutrons and
protons can form
a stable nucleus!

6. Forces of Nature
 Strong nuclear force: 1
 Electromagnetic 10−2
 Weak nuclear force 10−5
 gravity 10−39.
Why doesn’t the universe collapse into a single
nucleus?

7. Figure 1.2
Comparing Nuclear &
Electromagnetic Forces
V ∝1/r
V ∝exp(-r)/r
Nuclear Force, while strong, is short-ranged.

8. Binding Energy
 Masses of atoms are less than the sum of the masses of
their constituents.
 The missing mass is the energy binding them together,
as predicted by Einstein’s mass-energy equivalence:
E = mc2
 Binding energy per nucleon:
Eb =
W - M
A
é
ë
ê
ù
û
úc2

9. Figure 1.3
Binding energy per nucleon as a
function of mass number

10. Bohr’s Liquid Drop Model
 According to the liquid-drop model, the total binding
energy of nucleons is influenced by four effects
 a volume energy (the strong nuclear force)
 a surface energy (similar to surface tension)
 an excess neutron energy
 a coulomb energy (proton repulsion).
 B(A,I) = a1A – a2A2/3 – a3I2/4A – a4Z2/A1/3 + δ
 A: nuclear mass number, I: neutron excess number (N-Z),
a1 etc., constants, δ: odd-even fudge-factor

11. Figure 1.4
Contributions to Nuclear Energy as a
function of mass number

12. Odd-Even Effects, Magic
Numbers, and Shells
 Even combinations of nuclides are much more likely to
be stable than odd ones. This is the first indication that
the liquid-drop model does not provide a complete
description of nuclear stability.
 Another observation not explained by the liquid-drop
model are the so-called Magic Numbers. The Magic
Numbers are 2, 8, 20, 28, 50, 82, and 126.

13. Numbers of stable nuclei for odd
and even Z and N

14. The Shell Model of the
Nucleus
 The nucleus has shells, separate ones for protons and
neutrons.
 Consequently, much of nuclear stability is governed by ‘the last
nucleon in’, much as in the electron shell model of the atom.
 As in electron shells, shells accept neutrons and protons in
pairs with opposing spin, explaining odd-even effects.
 Pairing – having two nucleons of opposite spin in an orbit –
increases binding energy.
 Magic numbers reflect filling of shells.
 These in turn reflect solutions to the Schrödinger equation
for a three-dimensional harmonic oscillator.

15. Figure 1.5
Binding energy of isobars as a
function of neutron excess number

16. Figure 1.6
Binding energy of isobars as a
function of neutron excess number

17. Radioactive Decay
 Some combinations of protons and neutrons result in only a
metastable nucleus – one that eventually transmutes into an
other through loss (or more rarely gain) of a particle from the
nucleus.
 Beta decay (emission of electron or positron)
 a neutrino is also given off
 Electron capture
 (Some nuclei can decay in more than 1 possible way, e.g., 40K,
238U)
 Alpha decay (emission of a 4He nucleus)
 Fission
 All of these may be accompanied by emission of a high-energy
photon (a gamma ray) as the nucleus decays from an excited
state.

18. Rate of Decay
 Radioactive decay follows a first order rate law:
 (first order since it depends linearly on N, number of parent atoms)
 This is the basic equation of radioactive decay.
 λis the decay constant, unique to each unstable nuclide, and is
truly a constant, independent of everything (almost).
 Values vary of >20 orders of magnitude.
 The parent is said to be radioactive, the daughter radiogenic.
dN
dt
= -lN

19. Figure 1.8
Beta-decay

20. Beta decay and the neutrino
 The beta particle can have a range of energies, but with a
well-defined maximum.
 Seems to violate mass-energy conservation
 Beta decay involves a change in nuclear spin
 seems to violate momentum conservation
 To solve these problems, Fermi hypothesized the existence
of an essentially undetectable additional particle, the
neutrino (ν), that carried away the excess energy and
missing spin.
 The neutrino was eventually detected some 30 years later.
 Measuring ‘geoneutrinos’ is helping us define the composition
and energy production of the Earth.

21. Figure 1.7
alpha- and gamma-decay

22. Fission
 Yet another model of the nucleus
– the collective model –is
intermediate between the liquid
drop and shell models and
emphasizes collective motion of
nucleons.
 These motions can result in
nuclear shape becoming so
distorted it cannot recover and
breaks into (fissions) instead.
 This occurs only in the heaviest
nuclei, Th, U, and Pu. Among
naturally occurring nuclei, it is
almost exclusively 238U that
fissions.
 Reactors and bombs, however,
utilized ‘induced’ fission.

23. Nucleosynthesis
Origin of the Elements and the Secret
Lives of Stars

24. Figure 1.9
Abundances of the Elements

25. Questions
 How were the elements created? Were they
 created at the same time as the universe (in the Big
Bang)?
 created subsequently?
 What accounts for the observed (in meteorites and the
Sun) abundance of the elements?
 Abundance declines with atomic number
 Odd-even effects
 Some elements anomalously abundant

26. B2FH and Nucleosynthesis
 Physicists sought a single
mechanism for creation of the
elements but failed to find a
suitable one.
 Burbidge, Burbidge, Fowler and
Hoyle (1957) proposed the
elements were created in 4
ways/environments:
 Cosmological nucleosynthesis:
creation in the Big Bang
 Stellar nucleosynthesis: synthesis
of elements by fusion in stars
 Explosive nucleosynthesis:
synthesis of elements by neutron
and proton capture reactions in
supernovae
 Galactic nucleosynthesis:
synthesis of elements by cosmic
ray spallation reactions
Margaret Burbidge

27. Cosmological Nucleosynthesis
 Immediately after the Big Bang, the universe was too
hot for any matter to exist.
 But within a microsecond or so, it had cooled to 1011 K
so that matter began to condense.
 At first electrons, positrons, and neutrinos dominated,
but as the universe cooled and expanded, protons and
neutrons became more abundant. These existed in an
equilibrium dictated by the following reactions:
1H + e– ⇄ n + ν
n + e+ ⇄ 1H + ν
 As temperatures cooled through 1010 K, the reactions
above progressively favored protons (1H). In less than
two seconds things had cooled enough so that these
reactions ceased, freezing in a 6 to 1 ratio of protons to
neutrons.
 It took another 100 seconds for the universe to cool to
109 K, which is cool enough for 2H to form:
1H + 1n ⇋ 2H + γ
 Subsequent reactions produced 3He, 4He and a wee bit
of Li.
 Within 20 minutes or so, the universe cooled below 3 x
108 K and nuclear reactions were no longer possible.
 Some 380,000 years later, the universe had cooled to
about 3000 K, cool enough for electrons to be bound to
nuclei, forming atoms.

28. Figure 1.10
Hertzsprung-Russell Diagram

29. Stellar Nucleosynthesis
 When density of a forming star reaches 6 g/cm and T reached 10 to 20 million
K, hydrogen burning, or the pp process, can begin which involves reactions
such as:
1H + 1H → 2H + β+ + ν
2H + 1H → 3He + γ
3He + 3He → 4He + 21H + γ
 CNO cycle: carbon acts a nuclear catalyst to also synthesize 4He from 1H
 12C(p,γ) 13N(β++,γ) 13C(p, γ) 14N(p, γ) 15O(β+,ν) 15N(p,α) 12C
 limited to larger Pop. I stars
 These are the sources of energy sustaining main sequence stars.
 Little synthesis beyond He; some minor production/consumption of light nuclides,
particularly in the CNO cycle.

30. CNO Cycle
Figure 1.11

31. Stellar Nucleosynthesis in Red Giants
 Once the H is exhausted in the stellar core the interior collapses,
raising T and P.
 The exterior expands and cools. This is the red giant phase.
 When T reaches 108 K and density reaches 104 g/cc in the He
core), He burning begins:
4He + 4He → 8Be + γ
8Be + 4He → 12C + γ
 Because the t1/2 of 8Be is only 10-16 sec, 3He must collide
effectively simultaneously, which is why pressure must be so high.
 He burning also produces some O, 20Ne and 24Mg but Li, Be, and
B are skipped: they are not synthesized, rather they are consumed
in stars.
 Once He is consumed in the core, low mass stars such as the
Sun cannot reach T and P for heavier fusion reactions and they
end their lives as white dwarfs.
 Stars bigger than about 4 M☼ undergo further collapse and the
initiation of carbon burning when temperatures reach 600 million
K and densities 5 x 105 g/cc.
 For stars more massive than 11 M☼, about 1% of all stars,
evolution now proceeds at an exponentially increasing pace as
successive fusion reactions at higher T and P.
Evolution of a 25 solar mass
star.

32. s-process
 Red giant nucleosynthesis also
produces some free neutrons in
reactions such as:
 13C + 4He –> 16O + n
 22Ne + 4He –> 25Mg + n
 These neutrons can then be
captured by other nuclei in the
slow neutron capture (s) process.
 Because the neutron flux is low, a
capture will occur only every few
decades, so that gaps in nuclear
stability cannot be bridged as the
newly created unstable isotope
will decay before a second
neutron is captured.
Wikipedia

33. The e-process
 As the finale approaches, the star has become a cosmic onion of
sorts, with layers of heavier and heavier elements.
 A new core consisting mainly of 28Si has been created.
 At temperatures near 109 K and densities above 107 g/cc a
process known as silicon burning, or the e-process (for
equilibrium).
 This process is really a variety of reactions that can be
summarized as the photonuclear rearrangement of a gas
originally consisting of 28Si nuclei into one which consists
mainly of 56Ni, which then decays with a half-life of 6 days
to 56Fe, the most stable of all nuclei.
 The e-process includes reactions such as:
28Si + γ ⇄ 24Ne + 4He
28Si + 4He ⇄ 32S + γ
32S + 4He ⇄ 36Ar + γ
 While these reactions can proceed in either direction, there
is a tendency for the build-up of heavier nuclei with masses
32, 36, 40, 44, 48, 52, and 56, Partly as a result of the e-
process, these nuclei are unusually abundant in nature. A
variety of minor nuclei are produced as well.
 This continues for a few days at most. Finally, the inner core
has been converted completely to 56Ni and 56Fe, the latter
the most stable of all nuclei. Exogenic fusion reactions are
no longer possible.
Figure 1.13

34. Supernovae
 Once the star’s core is converted
to Fe, it can no longer resist
gravitational collapse and does so
at velocities of 25% of the speed
of light. Matter is consequently
compressed into neutrons. There
is a nearly instant rebound that
blows the star apart.
 The enormous flux of neutrons
created are rapidly captured by
surviving nuclei in the rapid
neutron capture (r) process.
 The extreme pressures and
energies also result in proton
capture (p-process), but it is
nonetheless less important than
neutron capture.
Chandra X-ray image of the
supernova remnant Cassiopeia A

35. Fun Facts about Supernovae
 Supernovae can have several
causes. We are mainly
interested in Type II.
 Most of the energy released in
a supernova is carried away
by neutrinos.
 Something like 10% of the
star’s mass is converted to
energy.
 A supernova produces enough
light to outshine an entire
galaxy for weeks or months.
Galaxy NGC 2770 NASA
image

36. R-Process Nucleosynthesis
Figure 1.15

37. Nuclides of s-, p-, and r-
processes
Figure 1.16

38. SN1987A in 2004
Figure 1.17

39. Galactic Nucleosynthesis
 Except for production of 7Li in the Big
Bang, Li, Be, and B are not produced in
any of the above situations.
 One clue to the creation of these
elements is their abundance in galactic
cosmic rays: they are overabundant by a
factor of 106.
 They are believed to be formed by
interactions of cosmic rays with
interstellar gas and dust, primarily
reactions of 1H and 4He with carbon,
nitrogen, and oxygen nuclei.
 These reactions occur at high energies
(higher than the Big Bang and stellar
interiors), but at low temperatures where
the Li, B and Be can survive.

40. Sample of Chart of the
Nuclides
Figure 1.19