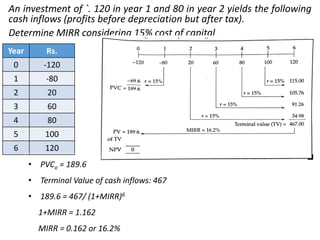
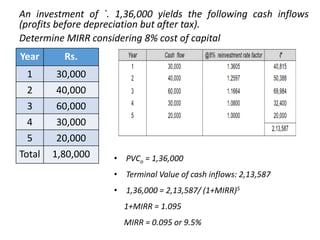
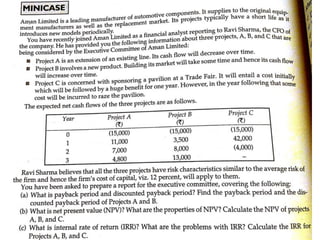
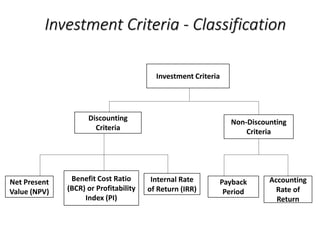
The document discusses various capital budgeting techniques used to evaluate investment projects. It covers topics like the capital budgeting process, investment criteria including payback period, accounting rate of return, net present value, internal rate of return and modified internal rate of return. It provides examples and outlines the key advantages and limitations of each technique.

1. Chapter 11
TECHNIQUES OF CAPITAL BUDGETING

2. OUTLINE
• Importance
• Capital Budgeting Process
• Project Classification
• Investment Criteria
• Payback Period
• Accounting Rate of Return
• Net Present Value
• Benefit Cost Ratio
• Internal Rate of Return
• Modified Internal Rate of Return

3. CAPITAL EXPENDITURES AND THEIR IMPORTANCE
 The basic characteristics of a capital expenditure (also referred to
as a capital investment or just project) is that it involves a current
outlay (or current and future outlays) of funds in the expectation
of receiving a stream of benefits in future
 Importance stems from
• Long-term consequences
• Substantial outlays
• Difficulty in reversing

4. CAPITAL BUDGETING PROCESS
• Identification of Potential Investment Opportunities
• Assembling of Investment Proposals
• Decision Making
• Preparation of Capital Budget and Appropriations
• Implementation
• Performance Review

5. PROJECT CLASSIFICATION
• Mandatory Investments
• Replacement Projects
• Expansion Projects
• Diversification Projects
• Research and Development Projects
• Miscellaneous Projects

6. Investment Criteria - Classification
Investment Criteria
Discounting
Criteria
Non-Discounting
Criteria
Net Present
Value (NPV)
Benefit Cost Ratio
(BCR) or Profitability
Index (PI)
Internal Rate
of Return (IRR)
Payback
Period
Accounting
Rate of
Return

7. Pay Back Period (PBP)
 Payback period is the length of time required to recover the initial cash outlay on the project.
 PBP tries to answer the question: How many years will it take for the cash inflows to pay the
original cost of investment?
 PBP in the above example would be 4 years as the end of 4th year the total of all cash inflows is
equal to the initial outlay.
• If the annual cash inflow of a project is a constant sum
PBP = (Initial Outlay) ÷ (Annual Cash Inflow)
• A project requires an initial outlay of Rs. 50,00,000 which generates a constant annual cash
inflow of Rs. 12,00,000. Then,
PBP = 50,00,000 ÷ 12,00,000 = 4.17 years
Year Cash Flows (in Rs.)
0 (2,50,000)
1 80,000
2 90,000
3 45,000
4 35,000
5 40,000

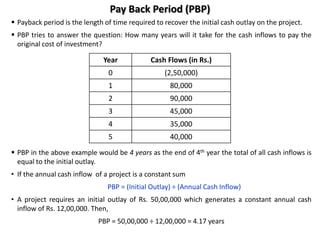
8. Pay Back Period (PBP)
• In certain projects if the annual cash flows are unequal, the calculation of PBP
becomes slightly complex.
• PBP of above project =
Lower Year + [(Outlay – CCFLL) ÷ (CCFUL – CCFLL)]
3 + [(1,35,000 – 1,15,000) ÷ (1,62,500 – 1,15,000)] = 3.42 years
Year 0 1 2 3 4 5
Cash Flows 1,35,000 30,000 40,000 45,000 47,500 50,000
Year Cash Flows (in Rs.) Cumulative Cash Flows (CCF) (in Rs.)
0 (1,35,000) -
1 30,000 30,000
2 40,000 70,000
3 45,000 1,15,000
4 47,500 1,62,500
5 50,000 2,12,500

9. Pay Back Period (PBP)
According to payback criterion, the shorter the payback period, the more desirable the
project. Firms using PBP specifies the maximum acceptable PBP.
PBP ≤ Benchmark PBP = Accept the Project
PBP > Benchmark PBP = Reject the Project
Merits:
 It is simple, both in concept and application. It does not involve any tedious
calculations and has few hidden assumptions.
 It is a rough and ready method for dealing with risks.
 A sensible criterion if the firm is pressed with the problem of liquidity.
Limitations:
 It fails to consider the time value of money, since projected cash flows are simply
added towards determining PBP.
 It ignores cash flows beyond the payback period. This leads to discrimination against
projects which generate substantial cash inflows in later years.
 It is a measure of capital recovery, not profitability.

10. Discounted Pay Back Period
• Overcomes an inherent shortcoming of PBP criterion by factoring in time value of
money into the analysis.
• Discounted PBP of above project =
Lower Year + [(Outlay – CCFLL) ÷ (CCFUL – CCFLL)]
3 + [(10,000 – 8,209) ÷ (10,941 – 8,209)] = 3.6 years
Year 0 1 2 3 4 5
Cash Flows -10,000 3,000 3,000 4,000 4,000 5,000
Year Cash Flows
(in Rs.)
Discount Factor
@10%
Present Value
(in Rs.)
Cumulative
Discounted Cash
Flows (in Rs.)
0 (10,000) - - -
1 3,000 0.909 2,727 2,727
2 3,000 0.826 2,478 5,205
3 4,000 0.751 3,004 8,209
4 4,000 0.683 2,732 10,941
5 5,000 0.621 3,105 14,046

11. Accounting Rate of Return
• An accounting oriented criterion of investment appraisal. It is also referred to as
‘Average Rate of Return’.
Profit after Tax ÷ Book value of Investments
• Numerator represents average annual post-tax profit over the life of the
investment/project, while the denominator is the average book value of fixed
assets committed to the project.
Accounting Rate of Return = 24,000 ÷ 70,000 = 0.342 = 34.2%
1 2 3 4 5 Average
Book value of inv (Rs.) 90,000 80,000 70,000 60,000 50,000 70,000
Profit after Tax (Rs.) 20,000 22,000 24,000 26,000 28,000 24,000
PROS:
• Simple.
• Based on accounting information
businessmen are familiar with.
• Considers benefits over the entire project
life.
CONS:
• Based on accounting profit, not cash
flow.
• Does not take into account the time
value of money.

12. NET PRESENT VALUE
The net present value of a project is the sum of the present value of all the cash flows
associated with it. The cash flows are discounted at an appropriate discount rate (cost of
capital)
NPV = ∑ Ct/(1+r)t - Initial Outlay
Ct = Cash flow at the end of year t;
r = Discount Rate or Cost of Capital
‘r’ reflects the risk of the project
Decision Rule:
NPV is a positive value = Accept the project
NPV is a negative value = Reject the project
NPV is exactly zero = Matter of indifference (Either Accept or Reject)
Between two independent projects having positive NPVs, the project with greater NPV will
be preferred by the organization.

13. Properties of NPV
 Net Present Values are additive.
 Intermediate cash flows are invested at the cost of capital.
 NPV calculation permits time varying discount rates.
 NPV of a conventional project decreases as the discount rate increases.
Pros:
 Reflects the time value of money
 Considers entire cash flow stream of the project.
 In sync with financial objectives of stockholder wealth maximization.
 NPVs are additive in nature enabling estimating NPV of a multi project
package. This eliminates chances of accepting poor projects combined with
another good project.
Cons:
 Is an absolute measure and not a relative hence does not factor in the scale of
investment.
 NPV rule does not consider the life of the project. In case of mutually exclusive
projects of differing lives, it is biased in favor of longer-term project.

14. Properties of NPV
 Net Present Values are additive.
 Intermediate cash flows are invested at the cost of capital.
 NPV calculation permits time varying discount rates.
 NPV of a conventional project decreases as the discount rate increases.
Time varying discount rates:
Year Cash Flows
Discount
rate
CF x PVFr
Present
Value
0 -12,000 -12,000
1 4,000 14%
4,000
1.14
3,509
2 5,000 15%
5,000
(1.14 ∗ 1.15)
3,814
3 7,000 16%
7,000
(1.14 ∗ 1.15 ∗ 1.16)
4,603
4 6,000 18%
6,000
(1.14 ∗ 1.15 ∗ 1.16 ∗ 1.18)
3,344
5 5,000 20%
5,000
(1.14 ∗ 1.15 ∗ 1.16 ∗ 1.18 ∗
2,344
NPV= ∑PVCI - PVCO 5,592

15. Benefit Cost Ratio or Profitability Index
 Benefit Cost Ratio (BCR) relates benefits offered by a project in terms of cash
inflows with the initial cost incurred.
 It represents ratio of the sum of present values of all cash inflows and initial
project outlay.
BCR = PVB ÷ Initial Outlay
PVB: Present Value of Benefits
Net BCR (NBCR) = BCR – 1

16. Benefit Cost Ratio – Suitability
• A school of thought suggests that since BCR measures NPV per rupee of outlay,
it can discriminate better between large and small investment proposals as
compared to standard NPV criterion.
• Weingartner studied validity of above argument. Findings were:
 Under unconstrained conditions, BCR and NPV will accept and reject same projects.
 When the capital budget is limited, BCR can rank projects correctly in the order of
decreasingly efficient use of capital.
 However, its use is not recommended owing to no possibility of aggregating smaller
projects and comparing with a larger one.
 If outlays occur beyond the current period, BCR criterion becomes unsuitable.

17. Internal Rate of Return (IRR)
• Internal Rate of Return of a project is the discount rate (r) which makes its NPV
equal to zero.
• It is the discount rate which equates the present value of future cash flows with
the initial investment.
• Value of ‘r’ in the following equation is IRR.
∑ Ct/(1+r)t - Investment = 0
Ct = Cash flow at the end of year t
r = Internal Rate of Return (or the discount rate)
NPV
• Assumes that the discount rate (cost
of capital) is known.
• Calculates the net present value,
given the discount rate.
IRR
• Assumes that the net present value is
zero.
• Figures out the discount rate that
makes net present value zero.

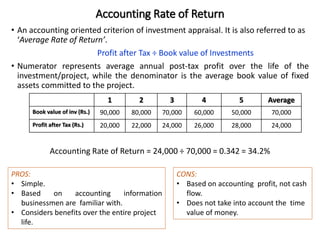
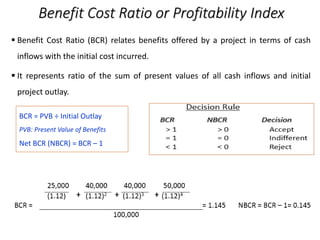
18. Internal Rate of Return (IRR)
Following are the projected cash flows of a proposed project
IRR is the value of ‘r’ which satisfies the following equation:
1,00,000 = [30,000/(1+r)] + [30,000/(1+r)2] + [40,000/(1+r)3] + [45,000/(1+r)4]
or 1,00,000 = 30,000 (PVIFr,1) + 30,000 (PVIFr,2) + 40,000 (PVIFr,3) + 45,000 (PVIFr,4)
Assume ‘r’ = 15%
30,000 (PVIFr,1) + 30,000 (PVIFr,2) + 40,000 (PVIFr,3) + 45,000 (PVIFr,4) = 1,00,801 > 1,00,000
Consider ‘r’ = 16%
30,000 (PVIFr,1) + 30,000 (PVIFr,2) + 40,000 (PVIFr,3) + 45,000 (PVIFr,4) = 98,636 < 1,00,000
IRR (or r) lies between 15% and 16%
Year 0 1 2 3 4
Cash Flow (in INR) (1,00,000) 30,000 30,000 40,000 45,000
= 15%
801
801+1364
x 16% - 15 %
IRR = 15.37 %

19. Merits and Limitations of IRR
Merits
 Easier to think in terms of rates of returns rather than absolute
rupee values.
 Easy interpretation by all stakeholders of the project.
 Non-requirement of prior knowledge of discount rate, unlike NPV
calculation.
Limitations
 Non-conventional Cash Flows.
 Mutually Exclusive Projects.
 Lending vs. Borrowing.
 Differences between short-term and long-term interest rates

20. NON-CONVENTIONAL CASH FLOWS
C0 C1 C2
-160 +1000 -1000
TWO IRRs : 25% & 400%
NPV
25% 400%
Discount rate( %)
NO IRR : C0 C1 C2
150 -450 375

21. MUTUALLY EXCLUSIVE PROJECTS
C0 C1 IRR NPV
(12%)
P -10,000 20,000 100% 7,857
Q -50,000 75,000 50% 16,964

22. MUTUALLY EXCLUSIVE PROJECTS
Project C0 C1 C2 C3 C4 IRR NPV
(at 10%)
X -1,10,000 +31,000 +40,000 +50,000 +70,000 22% 36,613
Y -1,10,000 +71,000 +40,000 +40,000 +20,000 25% 31,316

23. LENDING VS BORROWING
C0 C1 IRR NPV
(10%)
A (L) -4000 6000 50% 145
B (B) 4000 -7000 75% -236

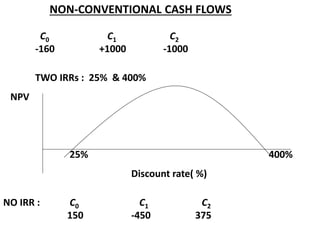
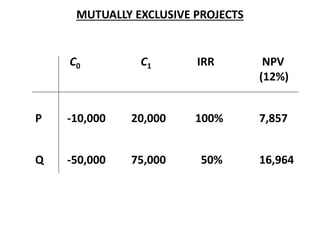
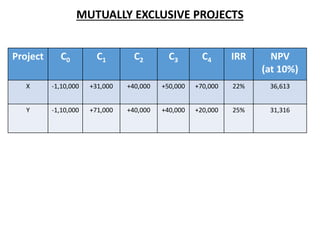
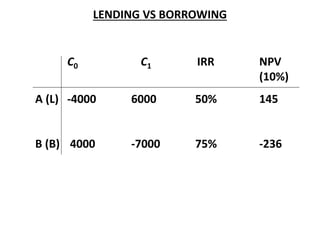
24. Modified IRR (MIRR)
• IRR assumes intermediate positive cash flows from a project are reinvested at its
IRR.
• This assumption generates inflated IRR estimates which may lead to selection of
inferior projects.
• (http://www.mckinsey.com/business-functions/strategy-and-corporate-
finance/our-insights/internal-rate-of-return-a-cautionary-tale)
• MIRR offers an improvement to traditional IRR enabling a more accurate
reflection of cost and profitability of a project.
• MIRR considers reinvestment of intermediate positive cash flows at the firm’s cost
of cost of capital, while initial outlay(s) are financed at firm’s financing cost.
MIRR = (Total FV of cash inflows @ cost of capital ÷ PV of initial outlay @ financing cost)1/n – 1
Two year project with an initial outlay of $195 and a cost of capital of 12% will return
$121 in year 1 and $131 in year 2. IRR vs MIRR ?
IRR = 18.66%, MIRR = [{121(1.12) + 131}/195]1/2 – 1 = 16.91%

25. An investment of `. 120 in year 1 and 80 in year 2 yields the following
cash inflows (profits before depreciation but after tax).
Determine MIRR considering 15% cost of capital
Year Rs.
0 -120
1 -80
2 20
3 60
4 80
5 100
6 120
• PVCo = 189.6
• Terminal Value of cash inflows: 467
• 189.6 = 467/ (1+MIRR)6
1+MIRR = 1.162
MIRR = 0.162 or 16.2%

26. An investment of `. 1,36,000 yields the following cash inflows
(profits before depreciation but after tax).
Determine MIRR considering 8% cost of capital
Year Rs.
1 30,000
2 40,000
3 60,000
4 30,000
5 20,000
Total 1,80,000 • PVCo = 1,36,000
• Terminal Value of cash inflows: 2,13,587
• 1,36,000 = 2,13,587/ (1+MIRR)5
1+MIRR = 1.095
MIRR = 0.095 or 9.5%

27. INVESTMENT APPRAISAL IN PRACTICE
• Over time, discounted cash flow methods have gained in importance and
internal rate of return is the most popular evaluation method.
• Firms typically use multiple evaluation methods.
• Accounting rate of return and payback period are widely employed as
supplementary evaluation methods.

30. Ans.
(b) Project P = 20.13% Project Q = 9.34%
(c) Choose P in both cases
(d) Project P = 18% Project Q = 10.41%

35. i) NPV = -1.361 ii) IRR = 11.18% iii) NPV = -0.136 iv) MIRR = 13.83%

36. Project A:
i) NPV = 28.34
ii) IRR = 17.29%
Project B:
i) NPV = 15.98
ii) IRR = 18.63%
Differential Project:
i) NPV = 12.37
ii) IRR = 16.42%