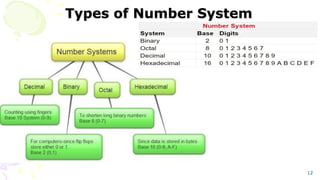
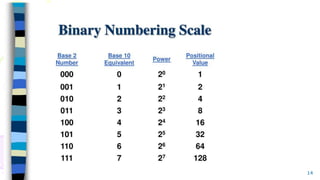
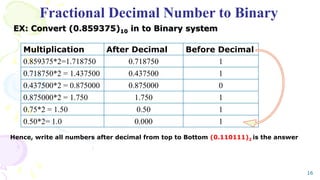
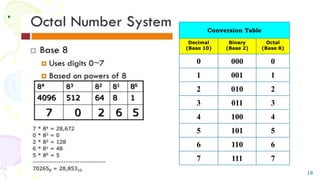
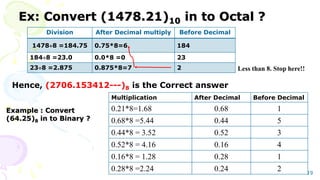
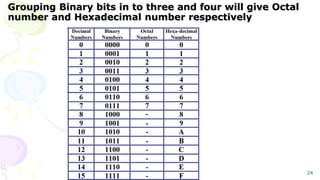
The document outlines the fundamentals of numerical methods and error estimation, explaining how errors arise in computer arithmetic and numerical calculations. It covers significant concepts such as true error, round-off error, truncation error, and the distinction between accuracy and precision. Additionally, it highlights the importance of numerical methods in various fields including engineering, computer science, and environmental studies.

1. 1
Well Come
Numerical Methods
(CEng-3112)

2. CHAPTER 1: BASIC CONCEPTS IN ERROR ESTIMATION
1.1 Computer Arithmetic
1.2 Sources of errors
1.3 Absolute and relative errors
1.4 Approximations of errors
1.5 Truncation errors and the Taylor series
1.6 Propagation of errors
http://numericalmethods.eng.usf.edu

3. specific objectives
After completion of this chapter, you will be able to:
 Understand how numbers are represented in digital computers
 Recognize how computer arithmetic can introduce and amplify round-off errors in
calculations
 Recognize the difference between true relative error εt, approximate relative error εa,
and acceptable error εs
 Understand the concepts of significant figures, accuracy, and precision.
 Recognize the difference between analytical and numerical solutions
 Recognize the distinction between truncation and round-off errors.
 Analyze how errors are propagated through functional relationships.
3

4. Introduction
Numerical technique is widely used by scientists and engineers to solve their
problems. A major advantage for numerical technique is that a numerical answer
can be obtained even when a problem has no analytical solution.
What are numerical methods and why should you study them?
Numerical Methods are techniques by which mathematical Problems are
formulated so that they can be solved with arithmetic and logical operations.
Because digital computers excel at performing such operations, numerical
methods are sometimes referred as computer mathematics”.
Beyond contributing to your overall education. there are several additional
reasons why you should study numerical methods:
Numerical analysis is concerned with the methods of finding the approximate
values and the absolute errors.
4

5. Reasons
1) Numerical methods are extremely powerful problem-solving tools. They
are capable of handling large systems of equations nonlinearities, and
complicated geometries that are not uncommon in engineering and science
and that are often impossible to solve analytically with standard calculus. As
such they greatly enhance your problem-solving skills.
2) Numerical methods allow you to use "canned“ software with insight. During
your career, you will invariably have occasion to use commercially available
pre-packaged computer programs that involve numerical methods. The
intelligent use of these programs is greatly enhanced by an understanding of
the basic theory underlying the methods. In the absence of such understanding
you will be left to treat such packages as “black boxes“ with little critical
insight into their inner workings or the validity of the results they produce.
5

6. Cont...
4) Numerical methods help to design your own program.
Many problems cannot be approached using canned programs. If you are
conversant with numerical methods, and are adept (very Skilled) at computer
programming, you can design your own programs to solve problems without
having to buy or commission expensive software.
5) Numerical methods are an efficient vehicle for learning to use computers.
Because numerical methods are expressly designed for computer implementation,
they are ideal for illustrating the computer's powers and limitations. When you
successfully implement numerical methods on a computer, and then apply them to
solve otherwise intractable problems, you will be provided with a dramatic
demonstration of how computer can serve our professional development. At the
same time, you will also learn to acknowledge and control the errors of
approximation that are part and parcel of large-scale numerical calculations.
6

7. Cont...
6) Numerical methods provide a vehicle for you to reinforce your
understanding of mathematics. Because one function of numerical methods is
to reduce higher mathematics to basic arithmetic operations. they get at the
"nuts and bolts" of some otherwise obscure topics. Enhanced understanding
and insight can result from this alternative perspective.
Where as
Mathematics, the science of structure, order, and relation that has evolved
from elemental practices of counting, measuring, and describing the
shapes of objects. It deals with logical reasoning and quantitative
calculation, and its development has involved an increasing degree of
idealization and abstraction of its subject matter.
7

8. Applications of numerical methods
in civil engineering
1. Used in structural Analysis to determine forces and moments in
structural systems prior to design
 2. Numerical methods provide an approximation that is generally good
enough. It is useful in all fields of engineering and physical sciences and
growing in utility in the life sciences and the arts Movement of
planets, stars and galaxies Investment portfolio management
Quantitative psychology Simulation of living cells Airline ticket
pricing, crew scheduling, fuel planning
3. Traffic Simulations: Collision avoidance, exit position, entrance, turning
point of vehicles are solved by forming mathematical model. Numerical
method is used to solve these mathematical models in traffic simulations. 8

9. Cont...
 4.Weather prediction: Numerical method is used to predict weather
and environmental simulations by data assimilation to produce
outputs of temperature, precipitation, and hundreds of other
meteorological elements from the oceans to the top of the
atmosphere.
 5. Ground water & pollutant movement: Ground water forms a part
of the hydrologic cycle. Numerical method is used to analyze the
movement of ground water and pollutants.
 6. Estimation of the amount of water: Numerical method is used to
estimate the amount of water that flows in a river, ocean current
during a year.
9

10. Cont....
 7. The usage of numerical methods in solving
differential equation in order to determine
the terminal velocity etc. in problems of statics and
dynamics.
 8. The usage of numerical methods in the problems of fluid
for example the solving of balance of flow at a junction for
incompressible fluid flow in pipes.
 9. The important used in the matrix methods of solving
various complex structural engineering problems involving
trusses, portal frames, beams etc
10

11. 1.1 Computer Arithmetic
Computer arithmetic is a field of computer science that investigates how
computers should represent numbers and perform operations on them. It includes
integer arithmetic, fixed-point arithmetic, and floating-point (FP) arithmetic, The
basic arithmetic Operations Performed by the Computer are addition (+),
Subtraction (-), Multiplication (x) and Division ()
And, logical operations are  ,  ,  ,  ,  ,  , , , , , , , , , ,
, , ,  ,  , etc....
The decimal numbers are first evolved to the machine numbers Consisting of
the only digits 0 and 1 with a base or radix depending up on the computer.
If the base is two, eight or sixteen the number system is called binary, Octal
or hexadecimal respectively.
11

12. Types of Number System
12

13. A) Decimal integer number
Decimal Number System is that number system in which a total of ten digits or ‘ten
signs’ (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) are used for counting/counting. This is the most
commonly used number system by humans.
For example, 645.7 is a number written in the decimal system.
Representation
4987 =(4987)10= 4000+900+80+7 = 4x103 + 9x102 + 8x101 + 7x100
4987.6251 =(4987.6251)10= 4000+900+80+7 = 4x103 + 9x102 + 8x101 + 7x100+6x10-1
+ 2x10-2 + 5x10-3 + 1x10-4
B) Binary number System
A binary number is a number expressed in the base-2 numeral
system or binary numeral system, a method of mathematical expression
which uses only two symbols: typically "0" (zero) and "1" (one)
called bits . The base-2 numeral system is a positional notation with a
radix of 2.
13

14. 14

15. Ex: Convert (58)10 in to binary number system
2 58 0
2 29 1
2 14 0
2 7 1
2 3 1
1
15
Start with 58 2
58 29 2
0 28 14 2
1 14 7 2
0 6 3 2
1 2 1 less than 2. Stop here!
1
Then, pick all the remainder from the last to the initial
(111010)2 is the Correct answer
Ex: Convert (1011.0011)2 in to decimal number system?
1875
.
11
)
2
1
2
1
2
0
2
0
(
)
2
1
2
1
2
0
2
1
(
)
0011
.
1011
(
10
4
3
2
1
0
1
2
3
2
























 




16. Fractional Decimal Number to Binary
EX: Convert (0.859375)10 in to Binary system
16
Multiplication After Decimal Before Decimal
0.859375*2=1.718750 0.718750 1
0.718750*2 = 1.437500 0.437500 1
0.437500*2 = 0.875000 0.875000 0
0.875000*2 = 1.750 1.750 1
0.75*2 = 1.50 0.50 1
0.50*2= 1.0 0.000 1
Hence, write all numbers after decimal from top to Bottom (0.110111)2 is the answer

17. C) Octal number System
17

18. .
18
Conversion Table
Decimal
(Base 10)
Binary
(Base 2)
Octal
(Base 8)
0 000 0
1 001 1
2 010 2
3 011 3
4 100 4
5 101 5
6 110 6
7 111 7

19. Ex: Convert (1478.21)10 in to Octal ?
Division After Decimal multiply Before Decimal
14788 =184.75 0.75*8=6 184
1848 =23.0 0.0*8 =0 23
238 =2.875 0.875*8=7 2
19
Hence, (2706.153412---)8 is the Correct answer
Example : Convert
(64.25)8 in to Binary ?
Multiplication After Decimal Before Decimal
0.21*8=1.68 0.68 1
0.68*8 =5.44 0.44 5
0.44*8 = 3.52 0.52 3
0.52*8 = 4.16 0.16 4
0.16*8 = 1.28 0.28 1
0.28*8 =2.24 0.24 2
Less than 8. Stop here!!

20. .
20
D)

21. .
21

22. 22

23. .
23
(Least Sig digit)
(Most Sig digit)
Example − Convert decimal number 98 into
octal number.
First convert it into binary or hexadecimal
number, = (98)10
=(1x26+1x25+0x24+0x23+0x22+1x21+0x20)10 or
(6x161+2x160)10
Because base of binary and hexadecimal are 2
and 16 respectively.
= (1100010)2 or (62)16
Then convert each digit of hexadecimal number
into 4 bit of binary number whereas convert
each group of 3 bits from least significant in
binary number.
= (001 100 010)2
or (0110 0010)2
= (001 100 010)2
= (1 4 2)8
= (142)8
Exercise:
Convert (456.824)10 to binary, Octal and
hexadecimal system?

24. Grouping Binary bits in to three and four will give Octal
number and Hexadecimal number respectively
24

25. 1.2 Sources of errors
25
In Numerical methods both accuracy and Precision are required for a
particular Problem.
We will use the Collective term error to represent both inaccuracy and
imprecision in our Predictions.
Numerical errors arise from the use of approximation to represent the
exact mathematical operations or quantities.
Consider the approximation we did in the problem of falling an object in
air. We observed some error between the exact (true) and numerical
Solutions (Approximation)
The relationship between them:
True Value (Tv) = Approximation + True Error
True Error = True Value – Approximate Value

26. Why we measure errors?
1) To determine the accuracy of numerical results.
2) To develop stopping criteria for iterative algorithms.
26
Errors and Approximations in Computation
A computer has a finite word length and so only a fixed number of
digits are stored and used during computation.
Exact number: number with which no uncertainly is associated to no
approximation is taken
Approximate number: There are numbers which are not exact.

27. Types of Errors
27
1) True Error: the difference between the true value in a calculation
and the approximate value found using a numerical method etc.
True Error = True Value – Approximate Value
2) Inherent Error : The inherent error is that quantity which is already present in
the statement.
3) Round-off error: is the quantity, which arises from the process of rounding
off numbers.
4)Truncation Error: These types of errors caused by using approximate
formulae in computation or on replace an infinite process by a finite one.
5) Absolute error: is the numerical difference between the true value of a
quantity and its approximate value.

28. 6) Relative True Error
 the ratio between the true error, and the true value.
𝐑𝐞𝐥𝐚𝐭𝐢𝐯𝐞 𝐓𝐫𝐮𝐞 𝐄𝐫𝐫𝐨𝐫 𝛜𝐫 =
𝐓𝐫𝐮𝐞 𝐞𝐫𝐫𝐨𝐫
𝐓𝐫𝐮𝐞 𝐯𝐚𝐥𝐮𝐞
7) Approximate Error: is defined as the difference between the present
approximation and the previous approximation.
9) Relative Approximate Error: Defined as the ratio between the
approximate error and the present approximation.
28
= Present Approximation – Previous Approximation
Approximate Error (Eapx)
Relative Approximate Error (Erapx)=
Approximate Error
Present Approximation

29. How is Absolute Relative Error used as a stopping criterion?
If ∈𝑎 <∈𝑠 , where s is a pre-specified tolerance, then no further
iterations are necessary and the process is stopped.
If at least m significant digits are required to be corrected in the
final answer, then
29
%
10
5
.
0
|
| 2 m
a





30. Significant digits or Figures
The significant digits of a number are the digits that have meaning or contribute to the
value of the number. Sometimes they are also called significant figures.
Which digits are significant?
There are some basic rules that tells you which digits in a number are
significant:
 All non-zero digits are significant
 Any zeros between significant digits are also significant
 Trailing zeros to the right of a decimal point are significant
30

31. Which digits aren't significant?
The only digits that aren't significant are zeros that are acting only as place
holders in a number. These are:
 Trailing zeros to the left of the decimal point (note: these zeros may or may not
be significant)
 Leading zeros to the right of the decimal point
31

32. Examples
32
10.0075 There are 6 significant digits. The zeros are all between significant
digits.
10.007500 There are 8 significant digits. In this case the trailing zeros are to the
right of the decimal point.
0.0075 There are 2 significant digits. The zeros shown are only place holders.
5000.00 There are 6 significant digits. The zeros to the right of the decimal
point are significant because they are trailing zeros to the right of a decimal
point. The zeros to the right of the 5 are significant because they are between
significant digits.

33. 1.3 Absolute, relative error, and Percentage error
Absolute : if X’ is the approximate value of quantity X then |X-X’| is
called the absolute error and denoted by Ea.
Therefore, Ea= |X-X’|
Relative Error : The relative error is defined as the ratio of the absolute
error of the measurement to the actual measurement.
∈𝒓=
𝑬𝒂
𝐓𝐕
=
𝑿 − 𝑿′
𝑿
Percentage error: The percentage error in X’ which is the
approximate value of X is given by
∈𝒑=∈𝒓∗ 𝟏𝟎𝟎 =
𝑿−𝑿′
𝑿
*100 33

34. Mean Absolute Error
The mean absolute error is the average of all absolute errors of the data
collected. It is abbreviated as MAE (Mean Absolute Error). It is
obtained by dividing the sum of all the absolute errors with the number
of errors. The formula for MAE is:
𝐌𝐀𝐄 =
𝟏
𝐧
𝐢=𝟏
𝐧
𝐗𝐢 − 𝐗
Here,
|xi – x| = absolute errors
n = number of errors
34

35. 1.4 Approximations of errors
The approximation error in a data value is the discrepancy between an exact value
and some approximation to it. This error can be expressed as an absolute error (the
numerical amount of the discrepancy) or as a relative error (the absolute error
divided by the data value).
Accuracy and precision are only two important concepts used in scientific
measurements.
 Accuracy refers to how close a measurement is to the true value. It reflects how
close a measurement is to a known or accepted value,
 Precision is how repeatable a measurement is. It reflects how reproducible
measurements are, even if they are far from the accepted value.
35

36. Error Approximation of a function
Let y =f(X1, X2-------Xn) be a function of two variables X1 and X2. If x1 and x2 are errors in
X1 , X2, the error y in y is given by:
Y + y = f(X1 +X1, X2 + X2 , ------- Xn +Xn)
 Error in Addition of Numbers
 Error in Subtraction of Numbers
 Error in Product of Numbers
 Error in Division of Numbers
36
we can get maximum absolute error and relative
error from these operations

37. Con’t...
The derivative , f’(x) of a function f(x) can be approximated by the
equation:
EX
If and h=0.30 ,
a) Find the approximate value of f’(2)? ,
b) Find the true value of f’(2)?
c) Find the true error for part (a)?
Solution: For X=2 , h=0.30
A)
=10.263
37
h
x
f
h
x
f
x
f
)
(
)
(
)
(
'



x
e
x
f 5
.
0
7
)
( 
3
.
0
)
2
(
)
3
.
0
2
(
)
2
(
'
f
f
f



3
.
0
)
2
(
)
3
.
2
( f
f 

b) The exact value of f’(2)
the true value of f’ (2)=9.514
C)
True error = True Value – Approximate
Value
x
e
x
f 5
.
0
7
)
( 
x
e
x
f 5
.
0
5
.
0
7
)
(
' 


x
e 5
.
0
5
.
3

722
.
0
263
.
10
5140
.
9 



3
.
0
028
.
19
107
.
22 


38. Inverse problem of the theory of errors
To find the error in the function u=f(x1, x2, x3, .......xn) is to have a
desired accuracy and to evaluate errors x1 , x2 , x3 ,........ xn in x1,
x2, x3, .......xn , We have ∆𝒖 = ∆𝒙𝟏 ∗
𝝏𝒖
𝝏𝒙𝟏
+ ∆𝒙𝟐 ∗
𝝏𝒖
𝝏𝒙𝟐
+--- +∆𝒙𝟏 ∗
𝝏𝒖
𝝏𝒙𝟏
Using the principle of equal effects which states , ∆𝒙𝟏 ∗
𝝏𝒖
𝝏𝒙𝟏
= ∆𝒙𝟐 ∗
𝝏𝒖
𝝏𝒙𝟐
=---=∆𝒙𝟏 ∗
𝝏𝒖
𝝏𝒙𝟏
This implies that ∆𝒖 = 𝒏 ∗ ∆𝒙𝟏 ∗
𝝏𝒖
𝝏𝒙𝟏
or ∆𝒙𝟏 =
∆𝒖
𝒏∗
𝝏𝒖
𝝏𝒙𝟏
, ∆𝒙𝟐 =
∆𝒖
𝒏∗
𝝏𝒖
𝝏𝒙𝟐
, ∆𝒙𝟐 =
∆𝒖
𝒏∗
𝝏𝒖
𝝏𝒙𝟐
..... Etc
Example: The percentage error in R is given by is not allowed to exceed
0.2% , find the allowable error in r and h , where r =4.5cm and h=5.5cm?
38

39. 1.5 Truncation errors and the Taylor series
Truncation errors are those that result from using an approximation
in place of an exact mathematical procedure.
These types of errors caused by using approximate formulae in
computation or in place of an infinite process by a finite one.
Taylor series The general form of the Taylor series is given by:
provided that all derivatives of f(x) are continuous and exist in the interval
[x,x+h]
Some Examples of tailor series
39
          











 3
2
!
3
!
2
h
x
f
h
x
f
h
x
f
x
f
h
x
f






!
6
!
4
!
2
1
)
cos(
6
4
2
x
x
x
x 





!
7
!
5
!
3
)
sin(
7
5
3
x
x
x
x
x






!
3
!
2
1
3
2
x
x
x
ex

40. 1.6 Propagation of errors (Propagation of Uncertainty)
It is defined as the effects of a function by a variables uncertainty. It is
denoted by:
In numerical methods, the calculations are not made with exact
numbers. How do these inaccuracies propagate through the
calculations?
40

41. Propagation of Errors In Formulas
 Propagation of error Addition
 Propagation of error Subtraction
 Propagation of error Product
 Propagation of error Division
If f is a function of several variables then the
maximum possible value of the error in f is
41
n
n X
X
X
X
X ,
,.......,
,
, 1
3
2
1 
n
n
n
n
X
X
f
X
X
f
X
X
f
X
X
f
f 
















 

1
1
2
2
1
1
.......