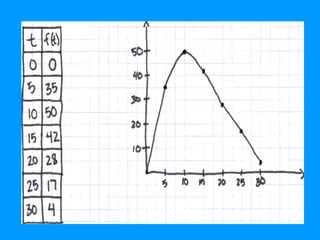
The document summarizes a calculus project about the rate at which students go through a lunch line over 30 minutes. It provides the following information: 1) Using a trapezoid Riemann sum, the total number of students going through the line from 0 to 30 minutes is calculated to be 868 students. 2) The average rate of students going through the line over this period is calculated to be 29 students per minute. 3) The acceleration of the lunch line from 5 to 10 minutes is calculated to be 3 students per squared minute.

1. Calculus Project By: Stacie Burke

2. The rate at which students go through a lunch line is shown in the following table and graph, f(t), where t is measured in minutes from 0 to 30. The rate is measured in students per minute.

4. a) Use a trapezoid Riemann sum to find how many students go through the lunch line from 0 to 30 minutes.

5. Solution: a) f(t) dt = 5(0 + 2(35) + 2(50) + 2(42) + 2(17) + 4) 2 = 868 students 0 30

6. Use the 6 even segments the data is divided into. Since the area of a trapezoid is (height x (base 1 + base 2))/2 you must find the area of each trapezoid and then add them all together. This will give you the number of students that went through the lunch line.

7. b) What is the average rate at which students go through the lunch line from 0 to 30 minutes? Round to the nearest whole number.

8. b) 1 f(t) dt = 1 868 = 30 30 29 students per minute 0 30 Solution:

9. To find the average rate you must first find the integral from 0 to 30 minutes and then divide it by 30. You divide by 30 because you are trying to find the average and 30 is the number of minutes you have total.

10. c) Find the acceleration of the lunch line from 5 to 10 minutes.

11. f(10) – f(5) = 50 - 35 = 3 10 – 5 5 3 students per squared minute Solution :

12. To find the acceleration from 5 to 10 minutes take the derivative. To find the derivative when there is no equation find the slope from 5 to 10. This will give you the acceleration in students per squared minutes.