Download as PDF, PPTX
![Introduction
Electromigration process
Conductance quantization
Experimental setup
Results
Conclusion
q Summary
q References
q Questions ?
François Bianco, July 10, 2007 Break junction - p. 35/35
Questions ?
Science has explained nothing; the more we know the more
fantastic the world becomes and the profounder the
surrounding darkness. [Aldous Leonard Huxley]
The important thing is not to stop questioning. [Albert Einstein]](https://image.slidesharecdn.com/breakjunctionslides-130808115834-phpapp02/85/Breakjunction-for-molecular-contacting-35-320.jpg)
Uploaded byFrançois Bianco
Breakjunction for molecular contacting
This document describes an experiment using electromigration to create break junctions for studying molecular electronics. The experiment uses electromigration to controllably break thin gold wires, creating nanoscale gaps. Conductance is measured through the gaps, showing quantization in units of the conductance quantum. Gap sizes were estimated from SEM images, ranging from less than 10nm to over 20nm. However, the feedback algorithm for controlling electromigration was unable to quickly detect the breaking point or prevent runaway breaking. Improved feedback methods are needed to better control gap formation and size.
Breakjunction for molecular contacting
- 1. François Bianco, July10, 2007 Break junction - p. 1/35 Break junction for molecular electronics using electromigration François Bianco
- 2. Introduction q Outline q Ideaand History q Realization Electromigration process Conductance quantization Experimental setup Results Conclusion François Bianco, July 10, 2007 Break junction - p. 2/35 Introduction
- 3. Introduction q Outline q Ideaand History q Realization Electromigration process Conductance quantization Experimental setup Results Conclusion François Bianco, July 10, 2007 Break junction - p. 3/35 Outline 1. Long terms goal and interest of molecular electronics 2. Electromigration process 3. Breaking phases 4. Quantization of the conductance 5. Experimental setup 6. Results s Conductance quantization s Electromigration process s Gap size s Critical power s Feedback algorithm 7. Conclusion
- 4. Introduction q Outline q Ideaand History q Realization Electromigration process Conductance quantization Experimental setup Results Conclusion François Bianco, July 10, 2007 Break junction - p. 4/35 Idea and History Idea s Use molecule as building block for passive and active electronic components s Extend the Moore’s law beyond the foreseen limit of common silicon electronics s Access to new quantum effects History s 1940 first theoretical explanation of charge transfer in molecules s 1988 theoretical single-molecule field-effect transistor s 1997 first measurement of a single molecule conductance
- 5. Introduction q Outline q Ideaand History q Realization Electromigration process Conductance quantization Experimental setup Results Conclusion François Bianco, July 10, 2007 Break junction - p. 5/35 Realization The first problem arising is the fabrication of molecular-scale electrical contacts. The use of: s Scanning tunneling microscope manipulation s Atomic force microscope manipulation s Mechanical break junction s or Electromigration break junction allows one to reach nanometer-spaced electrodes.
- 6. Introduction Electromigration process q History qDescription q Forces q Diffusion q Activation energy q Joule Heating Conductance quantization Experimental setup Results Conclusion François Bianco, July 10, 2007 Break junction - p. 6/35 Electromigration process
- 7. Introduction Electromigration process q History qDescription q Forces q Diffusion q Activation energy q Joule Heating Conductance quantization Experimental setup Results Conclusion François Bianco, July 10, 2007 Break junction - p. 7/35 History s Failure mechanism of small wires and electronics s Discovered more than 100 years ago by Gerardin a French scientist s Became practical only in the 60s for electronics design s 1968 James R. Black wrote his famous equation describing the mean time before failure due to electromigration3 (CC-BY-SA) Patrick-Emil Zörner
- 8. Introduction Electromigration process q History qDescription q Forces q Diffusion q Activation energy q Joule Heating Conductance quantization Experimental setup Results Conclusion François Bianco, July 10, 2007 Break junction - p. 8/35 Description Electromigration (EM) is the ion mass flux driven by a high electrical current density. s Due to collisions between the moving electrons and the ions s Two types of failure: x Open circuit x Short circuit
- 9. Introduction Electromigration process q History qDescription q Forces q Diffusion q Activation energy q Joule Heating Conductance quantization Experimental setup Results Conclusion François Bianco, July 10, 2007 Break junction - p. 9/35 Forces There is two forces acting on the ions s Electrostatics force due to the applied voltage Fe s Electron wind due to the momentum transfer from the electrons to the ions Fp F = Fe − Fp. = Z∗ eE (1)
- 10. Introduction Electromigration process q History qDescription q Forces q Diffusion q Activation energy q Joule Heating Conductance quantization Experimental setup Results Conclusion François Bianco, July 10, 2007 Break junction - p. 10/35 Diffusion The migration of ions takes place where the symmetry is broken like at: s the grain boundaries s the surface s or within the lattice at high temperature
- 11. Introduction Electromigration process q History qDescription q Forces q Diffusion q Activation energy q Joule Heating Conductance quantization Experimental setup Results Conclusion François Bianco, July 10, 2007 Break junction - p. 11/35 Activation energy Only the activated ions could participate to the diffusion, this is reflected by the temperature dependent diffusion coefficient: D = D0e −EA kT (2) where EA is the activation energy.
- 12. Introduction Electromigration process q History qDescription q Forces q Diffusion q Activation energy q Joule Heating Conductance quantization Experimental setup Results Conclusion François Bianco, July 10, 2007 Break junction - p. 12/35 Joule Heating The power dissipated in the junction P∗ = v∗2 Rj . (3) increase the local temperature accelerating the process by feedback mechanisms.
- 13. Introduction Electromigration process Conductance quantization qQuantization (1) q Quantization (2) q Breaking phases Experimental setup Results Conclusion François Bianco, July 10, 2007 Break junction - p. 13/35 Conductance quantization
- 14. Introduction Electromigration process Conductance quantization qQuantization (1) q Quantization (2) q Breaking phases Experimental setup Results Conclusion François Bianco, July 10, 2007 Break junction - p. 14/35 Quantization (1) To get a theoretical explanation of the quantization use the following steps 1. Solve the Schrödinger’s equation 2. Assumption translation symmetry in y direction 3. Separate the wavefunction 4. Plug the wavefunction into the current density Contribution to the current density of the electron in mode nky jnky = −e 1 L |χn(x, z)|2 ρ ky m∗ ey v (4) ρ charge carrier density, v the group velocity
- 15. Introduction Electromigration process Conductance quantization qQuantization (1) q Quantization (2) q Breaking phases Experimental setup Results Conclusion François Bianco, July 10, 2007 Break junction - p. 15/35 Quantization (2) The total current is the sum over ky and n. s Cross section determines the boundaries conditions s Use the Pauli Exclusion Principle s Possible n bellow the Fermi energy in the wire s Conductance shows plateaus at integer multiples of the conductance quantum G0 = 2e2 h .
- 16. Introduction Electromigration process Conductance quantization qQuantization (1) q Quantization (2) q Breaking phases Experimental setup Results Conclusion François Bianco, July 10, 2007 Break junction - p. 16/35 Breaking phases 1. Bulk regime -> continuous resistance (diffusive regime) 2. Intermediate steps 3. QPC -> discrete resistance due to the size reduction
- 17. Introduction Electromigration process Conductance quantization Experimentalsetup q Fabrication q Geometry and sizes q Four point measurement q Feedback algorithm Results Conclusion François Bianco, July 10, 2007 Break junction - p. 17/35 Experimental setup
- 18. Introduction Electromigration process Conductance quantization Experimentalsetup q Fabrication q Geometry and sizes q Four point measurement q Feedback algorithm Results Conclusion François Bianco, July 10, 2007 Break junction - p. 18/35 Fabrication s The junctions (d) –> EBM s The connection pads –> Photolithography
- 19. Introduction Electromigration process Conductance quantization Experimentalsetup q Fabrication q Geometry and sizes q Four point measurement q Feedback algorithm Results Conclusion François Bianco, July 10, 2007 Break junction - p. 19/35 Geometry and sizes The connectors are designed for minimizing the resistance for the voltage pads. We build two junctions with two different geometries: s Wire s Bowtie Device Geometry Length (nm) Width (nm) Thickness (nm) 1 & 2 wire 500 70 30 3 & 4 wire 500 75 30 7 & 8 wire 400 80 30 02 bowtie - 100 30
- 20. Introduction Electromigration process Conductance quantization Experimentalsetup q Fabrication q Geometry and sizes q Four point measurement q Feedback algorithm Results Conclusion François Bianco, July 10, 2007 Break junction - p. 20/35 Four point measurement Objective: reduce the error for the resistance measurement
- 21. Introduction Electromigration process Conductance quantization Experimentalsetup q Fabrication q Geometry and sizes q Four point measurement q Feedback algorithm Results Conclusion François Bianco, July 10, 2007 Break junction - p. 21/35 Feedback algorithm Goals: s EM in a controlled fashion s to reach the latest conductance plateau s and avoid a runaway of the EM Implementation: s Apply voltage ramps s Control the evolution with different feedback mechanisms x Resistance dR x Normalized conductance G/G0 x Normalized breaking rate 1 R ∂R ∂t
- 22. Introduction Electromigration process Conductance quantization Experimentalsetup Results q Electromigration q Quantization q Statistical occurence q Gaps sizes q Gaps sizes SEM (1) q Gaps sizes SEM (2) q Critical power (1) q Critical power (2) q Power feedback Conclusion François Bianco, July 10, 2007 Break junction - p. 22/35 Results
- 23. Introduction Electromigration process Conductance quantization Experimentalsetup Results q Electromigration q Quantization q Statistical occurence q Gaps sizes q Gaps sizes SEM (1) q Gaps sizes SEM (2) q Critical power (1) q Critical power (2) q Power feedback Conclusion François Bianco, July 10, 2007 Break junction - p. 23/35 Electromigration A->B : ohmic response B->C : controlled breaking C : break point
- 24. Introduction Electromigration process Conductance quantization Experimentalsetup Results q Electromigration q Quantization q Statistical occurence q Gaps sizes q Gaps sizes SEM (1) q Gaps sizes SEM (2) q Critical power (1) q Critical power (2) q Power feedback Conclusion François Bianco, July 10, 2007 Break junction - p. 24/35 Quantization Instabilities: fluctuation between allowed atomic arrangements
- 25. Introduction Electromigration process Conductance quantization Experimentalsetup Results q Electromigration q Quantization q Statistical occurence q Gaps sizes q Gaps sizes SEM (1) q Gaps sizes SEM (2) q Critical power (1) q Critical power (2) q Power feedback Conclusion François Bianco, July 10, 2007 Break junction - p. 25/35 Statistical occurence 8 measurements were added Non-integer value due to: s To small number of measured junction8 s Occurrence of non-integer value in Gold?
- 26. Introduction Electromigration process Conductance quantization Experimentalsetup Results q Electromigration q Quantization q Statistical occurence q Gaps sizes q Gaps sizes SEM (1) q Gaps sizes SEM (2) q Critical power (1) q Critical power (2) q Power feedback Conclusion François Bianco, July 10, 2007 Break junction - p. 26/35 Gaps sizes The sizes were approximated from SEM pictures. Size Number Yield < 10 nm 7 23% 10 − 20 nm 5 17% 20 − 50 nm 1 7% Low yields: Feedback take too long to detect the break point (0.1 to 1 s) Reorganization of the atoms the surface
- 27. Introduction Electromigration process Conductance quantization Experimentalsetup Results q Electromigration q Quantization q Statistical occurence q Gaps sizes q Gaps sizes SEM (1) q Gaps sizes SEM (2) q Critical power (1) q Critical power (2) q Power feedback Conclusion François Bianco, July 10, 2007 Break junction - p. 27/35 Gaps sizes SEM (1)
- 28. Introduction Electromigration process Conductance quantization Experimentalsetup Results q Electromigration q Quantization q Statistical occurence q Gaps sizes q Gaps sizes SEM (1) q Gaps sizes SEM (2) q Critical power (1) q Critical power (2) q Power feedback Conclusion François Bianco, July 10, 2007 Break junction - p. 28/35 Gaps sizes SEM (2)
- 29. Introduction Electromigration process Conductance quantization Experimentalsetup Results q Electromigration q Quantization q Statistical occurence q Gaps sizes q Gaps sizes SEM (1) q Gaps sizes SEM (2) q Critical power (1) q Critical power (2) q Power feedback Conclusion François Bianco, July 10, 2007 Break junction - p. 29/35 Critical power (1) v∗ = P∗ G(1 − GRs) (5) s Rs approximated as the start resistance s fitting parameter P∗ s use least-square algorithm
- 30. Introduction Electromigration process Conductance quantization Experimentalsetup Results q Electromigration q Quantization q Statistical occurence q Gaps sizes q Gaps sizes SEM (1) q Gaps sizes SEM (2) q Critical power (1) q Critical power (2) q Power feedback Conclusion François Bianco, July 10, 2007 Break junction - p. 30/35 Critical power (2) Geometry Mean critical power (µW) Standard deviation (µW) Wire 147 27 Bowtie 158 42 s Feedback mechanism not adapted s No good approximation for the series resistance s Wrong idea for the fitting
- 31. Introduction Electromigration process Conductance quantization Experimentalsetup Results q Electromigration q Quantization q Statistical occurence q Gaps sizes q Gaps sizes SEM (1) q Gaps sizes SEM (2) q Critical power (1) q Critical power (2) q Power feedback Conclusion François Bianco, July 10, 2007 Break junction - p. 31/35 Power feedback Feedback do not step down the voltage at a constant value : Conclusion: Feedback only prevents a runaway EM but is not able to detect it.
- 32. Introduction Electromigration process Conductance quantization Experimentalsetup Results Conclusion q Summary q References q Questions ? François Bianco, July 10, 2007 Break junction - p. 32/35 Conclusion
- 33. Introduction Electromigration process Conductance quantization Experimentalsetup Results Conclusion q Summary q References q Questions ? François Bianco, July 10, 2007 Break junction - p. 33/35 Summary Break junction s EM process observed s Quantization of conductance seen Feedback s Need to detect sooner the break point s No able to detect the EM but avoid a runaway of the process
- 34. Introduction Electromigration process Conductance quantization Experimentalsetup Results Conclusion q Summary q References q Questions ? François Bianco, July 10, 2007 Break junction - p. 34/35 References 1. Wikipedia 2. (CC-BY-SA) Patrick-Emil Zörner
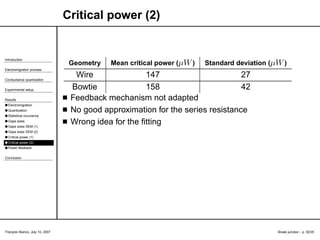
- 35. Introduction Electromigration process Conductance quantization Experimentalsetup Results Conclusion q Summary q References q Questions ? François Bianco, July 10, 2007 Break junction - p. 35/35 Questions ? Science has explained nothing; the more we know the more fantastic the world becomes and the profounder the surrounding darkness. [Aldous Leonard Huxley] The important thing is not to stop questioning. [Albert Einstein]