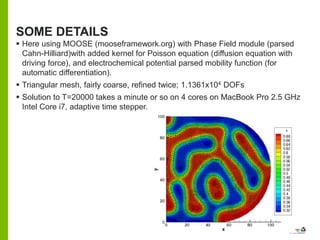
This document provides an update on Benchmark 6, which models the flow of a charged concentration field using a coupled Cahn-Hilliard-Poisson formulation. The previous formulation was unsatisfactory, so changes were made to make the model more physical and different from a block co-polymer problem. The new formulation includes a concentration-dependent mobility, neutralizing background charge, applied external field, and zero particle and charge flow boundary conditions. Some tests were run in MOOSE to check that the solution behaves reasonably by tuning parameters like the dielectric constant and mobility.

1. BENCHMARK 6 UPDATE
drhgfdjhngngfmhgmghmghjmghfmf
OLLE HEINONEN, ANDREA JOKISAARI, JIM WARREN, JON GUYERS, PETER VOORHEES
Sept. 25, 2018
Center for Hierarchical Materials Design http://chimad.northwestern.edu/about/index.html

2. BACKGROUND
 Benchmark 6 is a simple model of flow of a charged concentration field.
 Technically, it is a coupled Cahn-Hilliard-Poisson problem: the concentration field
flows under forcing of an electrochemical potential which contains contributions from
the electrostatic field generated by the charge distribution.
 Previous formulation was unsatisfactory:
– One one type of charge so the system was not charge-neutral.
– Original model was technically identical to a block co-polymer problem –
desirable to make it a little different
 The boundary conditions (zero flow of concentration field across boundaries,
Dirichlet BC for the electrostatic field) where not quite physical: the particle flow and
charge flow are linked (Einstein relation) so a particle flow across boundary has to
have a concomitant charge flow across boundary.
 It is desirable (but not absolutely necessary) to have the total energy of the system
be monotonically non-increasing. This is generally not the case if there is flow
across the the boundaries (external field does work on the system).
2

3. New formulation
 Same geometries: (i) square 100 x 100 units, and square+halfmoon (rectangle
50 x 100 units and half-circle radius 50 nm attached)
 Concentration-dependent mobility 𝑀 𝑐 =
𝑀0
1+𝑐2 to make it a little bit more
interesting (also rather physical for ionic flow).
 Neutralizing uniform background charge density 𝑐0 with total magnitude of
charge same as initial total charge of concentration field 𝑐
 Applied external field Φ 𝑒𝑥𝑡 such that ∇2
Φ 𝑒𝑥𝑡=0.
 Zero particle and charge flow across boundaries.
 Pseudo-random initial concentration field with average concentration close to 0.5
3

4. FREE ENERGY
 Free energy contains contributions from bulk chemical energy, gradient in the
concentration field (standard spinodal decomposition), and electrostatic free
energy:
𝑓𝑒𝑙𝑒𝑐=
1
2
𝜌Φ𝑖𝑛𝑡 + 𝜌 Φ 𝑒𝑥𝑡
where Φ 𝑡𝑜𝑡= Φ𝑖𝑛𝑡 + Φ 𝑒𝑥𝑡 is the total electrostatic potential, and 𝜌 = 𝑘 𝑐 − 𝑐0 with k
a constant
4

5. EQUATIONS
The equations to be solved are then
where Φ = Φ 𝑡𝑜𝑡=Φ𝑖𝑛𝑡+ Φ 𝑒𝑥𝑡 because it was easy to copy latex images and I hate
writing equations using ppt.
Boundary conditions:
 No particle current across boundaries ∇𝜇 ∙ 𝑛=0
 No charge current across boundary:
 External potential Φ 𝑒𝑥𝑡 = 𝐴𝑥𝑦 + 𝐵𝑥 + 𝐶𝑦
5

6. SOME DETAILS
 Here using MOOSE (mooseframework.org) with Phase Field module (parsed
Cahn-Hilliard)with added kernel for Poisson equation (diffusion equation with
driving force), and electrochemical potential parsed mobility function (for
automatic differentiation).
 Triangular mesh, fairly coarse, refined twice; 1.1361x104 DOFs
 Solution to T=20000 takes a minute or so on 4 cores on MacBook Pro 2.5 GHz
Intel Core i7, adaptive time stepper.
6

7. SOME SANITY CHECKS (MOOSE)
 First set Dirichlet BC on total
potential, Φ 𝑡𝑜𝑡 = 0 on
boundaries, Φ 𝑒𝑥𝑡=0
7
Then use Neumann conditions on
electrostatic potential, Φ 𝑒𝑥𝑡=0
Note that Neumann BC are integrated
in MOOSE: the BC is not satisfied at all
points, but only the integral over each
boundary.

8. MORE SANITY CHECKS
8
Tune the relative strength of electrostatic to chemical forces with
the dielectric constant 𝜀. For 𝜀 = 1 electrostatic energy large so
system should go to uniform density for minimal electrostatic
energy
Already at timestep T=20 the concentration field is uniform

9. …and more
 For 𝜀 = 100 the electrostatic energy is insignificant compared to chemical
energy. System should do spinodal decomposition.
9
Increase mobility by factor of 2, extend
time to T=20000

10. With external potential
10
Here at T=1500
Concentration field (Total) Electrostatic potential
Laplacian of potential −𝑘(𝑐 − 𝑐0)/𝜀

11. Tuning dielectric constant (T=1500)
11
𝜀 = 10
𝜀 = 5
𝜀 = 2

12.  Re-formulated coupled Cahn-Hilliard-Poisson problem to make it a little bit more
physical
 A few simple tests to see if solution makes sense
 Note: Solutions I use pass smell-test but not sure about calculation of total
energy (which is why I did not show any total energy plots). For that matter, there
could be other bugs, too…..
 Runs very fast with
12
Summary

13. OUTLINE
13

15. www.anl.gov